算符优先文法分析器_编译原理：LL, LR 文法浅析

编译原理-文法

编译原理文法这里有很多混淆的地方，在这里梳理一下，尤其是各种“文法”（LL(k), SLR(k), LALR(k), LR(k), unambiguous grammar, ambiguous grammar, context-free grammar）。

首先说明，Context-free grammar与无二义性文法不是一个层级的概念。CFG的意思是：我们用产生式设计的一组文法，对于每一个推导，其中的NT可以任意地被产生式右部替换而合法（这并不限制对于一个文本，只能推理出一棵树）。也就是每个NT之下的产生式是等价的，比如对于Verb->吃/睡/飞，在具体解析时，不论前面的主语/后面的宾语是什么，都合法。二义性是在CFG之下的概念。

Table of Contents

• 编译原理-文法
  • 1. 文法的之间关系，以及原因。
    • LL 与 LR 文法的差异
    • LL(0)/LR(0)是什么？
    • SLR(0), LR(0), SLR(1), LR(1)的区别？
  • 2. parse过程的二义性问题、一些当代的解决方案

疑惑主要在于这一点：

1. 各类文法的“包含”关系，以及原因。

LL(0) < LL(1) < LR(1)
LL(0) < LR(0)
LR(0) 与 LL(1) 是 有交集，不相互包含的关系。

此外，LL(k)/LR(k) < unambiguious grammar < All CFGS

Stackoverflow: LL(1) 与 LR(0)的关系

LL 与 LR 文法的差异

这个视角很好的解释了LL算法和LR算法的差异： Blog: ll-and-lr-parsing-demystified

树的遍历

对于自己，有必要先回顾一下树的遍历的一些性质。树是一种简单的图，它有两个维度的结构，父子关系和兄弟关系（从左至右的相对关系）；遍历得到的串是一维的，因而只能保留一个维度的信息（进而，由遍历复原（二叉）树，需要两种遍历，并必须需要中序遍历）。对于二叉树，先序遍历与后序遍历提供了父子关系这一维度，最基本的确定了根，中序遍历提供了兄弟的关系。对于表达式树（运算符都是二元的），内部结点都是操作符、叶子节点都是运算数，其先序与后序遍历保留了相应信息，所以不需要优先级就可以正确运算（直观上理解）。

语法树不是二叉树，但它的每个结点的孩子是被文法确定的。它先序遍历与后序遍历，两者看似应无差别。但我们读取输入缓冲时，是确定地从左至右读取，进而导致了两者的差异。并且注意LL、LR都是online算法，是伴随输入的不断进行，不断产生输出的。

遍历 与 LL, LR

我们在parse的时候，实际上就是想最终得到正确的父子关系，其实对应的就是先序遍历与后序遍历所关注的这个维度。也实际上，把Parser当做一个黑箱，就是在输入序列中找到确定位置插入内部结点，使之称为树的先序或后序遍历。先序遍历（LL）的父节点在子节点的左边，（并由于是在线算法，所以只lookahead有限个），他需要通过lookahead猜测后面的孩子的父亲是谁，提前插入；而后序遍历（LR）是已经看完了孩子，lookahead只是决定要插入这个父节点还是另一个。所以，在lookahead相同的情况下，LR比LL的优势是，它看完全了子节点。（课程里用的术语是句柄，其实就是“孩子啦”。）。所以LR(k)文法是严格大于LL(k)的。

但要指出，LL算法虽然适用的文法更小，但它可以更好的结合一些extension，因为它是从“大局”着手的，自顶向下，比如智能编译器。
LL算法可以很好地处理语义分析的继承属性。
不过个人认为，LR可以很好地解决困扰，比如在得到每棵子树时，保证其下所有的内部依赖(已经可以计算的继承属性)算出来即可（因为CFG是确定的嘛）。

LL(0)/LR(0) 是什么？

根据前面所述，LL(0)算法相当于要不根据任何信息，猜测使用的产生式，所以无实用价值。而LR(0)，它仍获得了孩子的信息，只不过它只根据看到的孩子，（而不lookahead，像规范LR(1)，SLR(1)那样），做出reduce动作。它仍可以表达很多文法。

SLR(0), LR(0), SLR(1), LR(1) 的区别？

SLR 与 规范LR、LALR，个人认为是利用lookahead的字符的方式不同而已。在数学层面SLR(0)应等同于LR(0)。

Stackoverflow中一个不错的问题。

2. parse过程的二义性问题，当代应用背景的parse techniques

Blog: LL and LR in Context: Why Parsing Tools Are Hard

这一篇讲述了二义性导致的各种各样的难题，说明了一些现代的解决方案。最终又回归说LL, LR的好。

主要讨论点在于，判定一个文法是或不是unambigious，是undecided的问题。通过形式化地引入“优先级”，可以hide这个问题，但这只是回避了二义性。LL, LR算法可以确定一个文法是unambigious的（只要表没有冲突的话），进而保证线性的复杂度；但它们不能适用于所有的unambigious的文法：因为只是lookahead k，在表格中发现冲突时，不能确定是由于文法的二义性、还是算法的能力导致的（不过感觉人类设计的CFG都不会这么lookahead特别多吧QAQ。。）。

GLR可以分析任意的CFG、输出所有的AST供用户选择，（我认为它就是LR(∞)...），但它并不要先建“表”，对于一个文法是否是二义性的，它不能在仅看到文法时就了解（它根本不处理文法，它只是在做完全的遍历）。所以GLR并不能判断文法的二义性。

就是这张图!

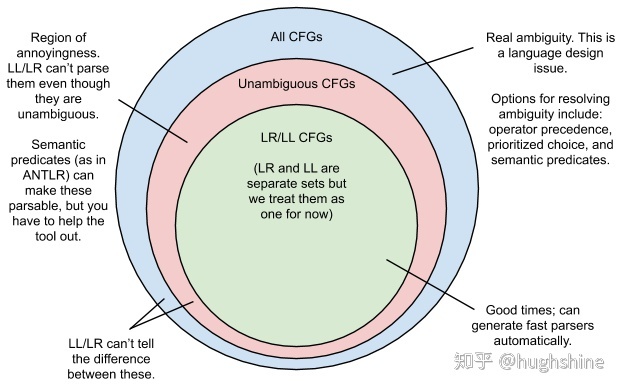
文中另提及了一些拓展LL, LR的方式，和其他算法，不在此处提及，不过值得一看。

2020年7月4日更新