本文补充介绍了多种聚类方法，包括k-中心点聚类，其使用中位数代替均值；BIRCH，通过聚类特征树实现多阶段聚类；Chameleon，利用动态建模的多阶段层次聚类；以及概率层次聚类，基于概率模型的聚类分析。此外，还提到了网格聚类方法如STING和CLIQUE，以及处理高维数据的双聚类和谱聚类。这些方法在处理不同特性的数据集时各有优势，适用于不同的聚类需求。
关于一些常见的聚类问题，之前的文章有详细说明过，可以参考
大饼：机器学习之7——聚类(Clustering)zhuanlan.zhihu.com这篇文章主要补充一些之前没有提到过的其他聚类方法。
k-中心点聚类
这是对于k均值聚类的一个补充，我们知道，k均值聚类选择簇的方式是样本点的均值，距离度量方式为欧氏距离，k中心点聚类的距离度量方式是
- 从D中随机选取k个对象作为初始的代表对象；
- repeat：
- 将每个剩余的对象分配到最近的代表对象所代表的簇；
- 随机选择一个非代表对象
；
- 计算用其替换代表对象
的总代价
；
- 如果代价更小，就替换当前代表对象，并形成新的k个簇
- 否则不发生变化，重新repeat；
BIRCH：使用聚类特征树的多阶段聚类
每个簇的聚类特征（CF）是一个三维向量，汇总对象簇的信息：
利用以上信息可以统计一些统计量，比如簇的形心
R代表成员对象到形心的平均距离，D是簇中逐对对象之间的平均距离。
优势有以下两点：
- 用聚类特征来概括簇可以避免存储个体对象的详细信息；
- 聚类特征线性可加，如果两个簇要合并，那么两个簇的聚类特征可以依次线性相加；适合增量聚类；
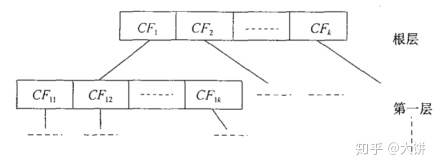
上图为CF树，从根结点依次往下，分别存储每个簇的聚类特征，每个非叶子结点都有自己的子女（子簇）的聚类特征汇总，依次往下层次化铺开，可以看成是对数据的多层压缩。
刚开始对于叶结点进行聚类，将稀疏簇当作离群点删除，剩余的簇合并为更大的簇，直到根节点，形成一颗完整的CF树。
这种聚类方式在球状簇数据中表现很好（因为通过R和D设置阈值控制树的生成），并且支持增量聚类，具有线性可伸缩性。
Chameleon：使用动态建模的多阶段层次聚类
如果两个簇的互连性都很高并且之间有靠得很近就将其合并。Chameleon不用依赖于一个静态的用户提供的模型，能够自适应合并簇的内部特征。
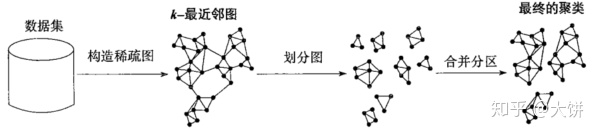
如上图所示，先用k-最近邻图构建一个稀疏图，每个顶点作为一个数据对象，如果另一个对象是其k个最相似的对象之一那么就会有一条边。这些边通过加权来反映对象间的相似度。Chameleon使用图划分方法，把k-最近邻图划分为大量相对较小的簇。簇C被划分成子簇Ci和Cj，使得被切断的权重之和最小。
然后使用凝聚层次聚类算法，基于子簇的相似度反复合并子簇，这里的相似度综合考虑互连性和邻近性。
相互连接度
相互接近度
Chameleon在发现高质量的任意形状的簇方面具有更强的能力。
概率层次聚类
用来解决聚类问题的三类问题：
- 层次聚类好的距离度量选择；
- 数据对象不能有缺失的属性值，否则无法计算距离；
- 大部分层次聚类是启发式，局部搜索好的合并/划分，导致聚类层次结构的优化目标不清晰
概率层次聚类的任务是使用待聚类的观测数据为对象。尽可能准确地估计生成模型。实际中可以假定数据生成模型为常见的分布函数，比如高斯函数等。学习生成模型的任务就是找出使得模型最佳拟合观测数据集的参数值。（统计学知识：根据观测值计算最大似然函数，估计分布模型的参数）
度量两个簇之间的距离：
概率层次聚类先从每个对象为一个簇开始，如果两个簇之间的距离为负，则合并，每次迭代过程中，我们试图找到Ci和Cj，
只要
概率层次模型的一个优点在于，如果数据集有缺失值，可以在每个维度上使用该维度的观测值独立学习一个高斯模型。
网格聚类方法
目前介绍的聚类方法都是由数据驱动的，空间聚类方法不受数据影响，而是采用空间驱动的方法，将嵌入空间划分为独立于输入对象分布的单元。
STING：统计信息网路
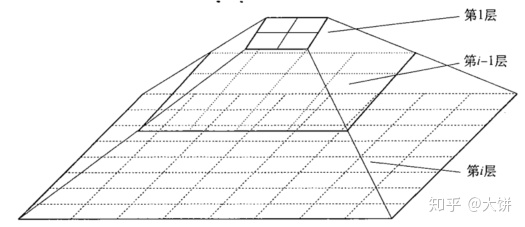
每个网格单元的属性统计信息（mean、maxmin、distribution等）被作为统计参数预先计算和存储。高层单元的统计参数可以很容易的从低层单元的参数计算得到。最底层单元的属性统计信息由数据计算，distribution可以由用户指定或者通过假设检验来获得，高层单元的分布类型基于对应的低层单元多数的分布类型，用阈值过滤过程的合取来计算。
统计参数的使用按照自顶向下的网格方式，首先选取单元数较少的高层的那元，计算该单元与给定查询相关程度的置信区间，只考虑具有相关性单元，接着将相关性单元映射到低层，只检查较高层相关单元所映射到的低层单元，直至到最底层。
STING优点：
- 基于网格的计算是独立于查询；
- 网格结构有利于并行处理和增量更新；
- 效率高，聚类复杂度O(n)，查询复杂度O(g)，g是最底层网格单元数目。
但是此方法在构建父亲单元时没有考虑子女单元和其相邻近单元之间的联系。
CLIQUE：类似于Apriori子空间聚类方法
数据往往由着数十种属性，其中很多可能互相是不相关的，这些因素使得我们很难在整个数据空间找出簇，在数据的不同子空间搜索簇可能会更有意义。比如在健康领域，患者记录包含大量属性来描述个人信息、大量症状、身体状况、家族病史等，找出所有甚至大部分属性上非常一致的患者群是不大可能的。
CLIQUE用于发现子空间中基于密度的簇它把每个维度划分为不重叠的区间，从而把数据对象的整个嵌入空间划分为单元。并且使用到一个密度的阈值来识别稠密单元和稀疏单元。
- 将d维空间划分为若干互不重叠的矩阵单元，扫描所有网络，当发现第一个稠密单元，便开始以此扩展，扩展原则是若一个单元与已知稠密单元邻接并且自身也是密集，则将该单元加入其中，直到不再有符合条件的单元为止；
- 在k维的子空间中，将每个k-1维的稠密单元区间进行组合，并保留密度大于密度阈值的重叠结果，一旦计算k-1维度的稠密单元，可以通过最后k-1个候选者的所有组合来扩展到k维度
CLIQUE可以自动发现含有高密度簇的最高维子空间，当数据维度增加时也有良好的可伸缩性，但是聚类结果非常依赖于预先设定的网格大小和密度阈值。
霍普金斯统计量
在给数据集做聚类之前，我们需要事先评估数据集的聚类趋势，要求数据是非均匀分布，均匀分布的数据集没有聚类的意义。
霍普金斯统计量可以检验空间分布的变量的空间随机性：
- 等概率随机的从D空间中抽取n个点
，D空间中每个点以相同的概率包含在样本之中，对于每个点
，找出其在D空间中的最近邻，得到距离：
- 等概率随机的从D空间中抽取n个点
，D空间中每个点以相同的概率包含在样本之中，对于每个点
，找出其在
空间中的最近邻，得到距离：
- 计算霍普金斯统计量H：
如果H大约为0.5左右，说明D接近均匀分布，如果是高度倾斜，则H将接近于0。
关于对象同时属于多个簇的研究
模糊簇
单个对象被划分到多个簇的隶属度
其中
对象与其被指派到簇的中心之间的距离或相似度也可以用来度量该对象属于簇的程度。
对于对象
其中参数p控制隶属度的影响，p值越大隶属度影响越大。
簇
最后聚类
可以用来度量模糊聚类对数据集的拟合程度。
概率簇
假定聚类的类别是数据空间的一个分布，可以使用概率密度函数精确表示。对于一个概率簇C，它的密度函数f和数据空间的点o，
我们假定数据集D中的每个观测样本都是由以下两步所产生：
- 按照概率
选择一个簇
- 按照
的概率密度
，选择一个
的实例
其中
这里其实假定了每个样本由混合模型所产生，即样本集合是来自多个概率簇的实例的混合。
给定数据集D和所要求的簇数k，基于概率模型的聚类分析的任务是推导出使用以上数据最可能产生数据集D的k个概率簇。
考虑k个概率簇
现在的任务是，找出k个概率簇的集合C，使得
设
那么全部的数据集可以改写为：
推导出其值最大化的参数集合
期望最大化算法
- 期望步：根据当前的模糊聚类或概率簇的参数，把对象指派到簇中；
- 最大化步：发现新的聚类或参数，最小化模糊聚类的SSE或基于概率模型的聚类期望似然
K-means聚类就是一种典型的期望最大化算法。但是不同的是这里的EM算法将应用于模糊聚类，即一个样本可能属于多个类别。
- 先指定k个簇，分别计算样本o到每个簇的隶属度：
- 极小化SSE，并调整形心：
(坐标x，y单独计算)，这里的o对应于x或y的坐标值。
- 重复以上步骤直至不在收敛；
聚类高维数据
双聚类
双聚类的使用场景在于，对于一个具有二维矩阵的数据集，通过对行聚类或者列聚类都能发现有价值的信息（比如推荐系统中的协同过滤）。
传统的聚类方式，可能对于一个nxp的数据集矩阵，每一行都是一个样本，每个样本由p个特征值所组成，那么研究如何利用这p个特征值来将n个样本进行聚类，双聚类是指，不仅根据p列的特征值对n个样本进行聚类，同时也会根据n行的样本来进行p个特征的聚类，最后形成一个子矩阵簇。
对于一个子矩阵
第j列的均值是：
子矩阵所有元素均值：
均方残差：
谱聚类
- 使用距离度量计算相似矩阵W，使得
- 使用相似矩阵W，导出矩阵
，比如在Ng-Jordan-Weiss方法中，定义一个对角矩阵
，其中
是W第i行之和：
，那么
- 找出A的前k个具有最大特征值的特征向量。
- 将原数据投影到前k个特征向量定义的新空间，并运行诸如k-means聚类算法找出k个簇
参考书籍：
《Data Mining——Concepts and Techniques Third Edition》
扫一扫
1023
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
