数据结构-图-有向无环图-关键路径查找

于 2020-07-27 16:13:31 发布
阅读量404 收藏
点赞数
分类专栏： 数据结构 文章标签： 链表 数据结构 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_39518639/article/details/107612811
版权

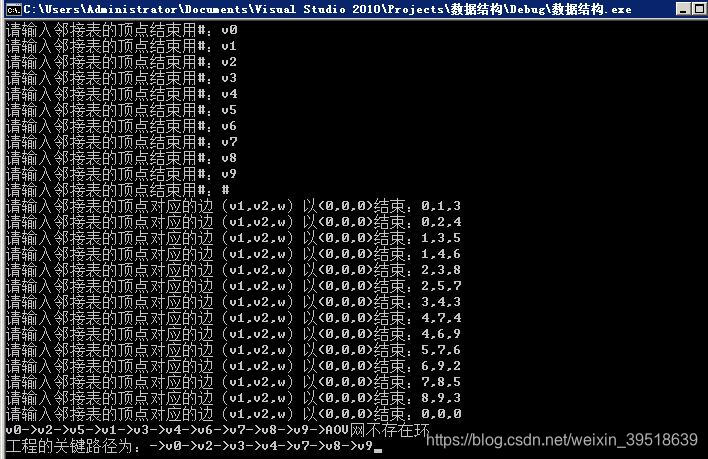
在这里插入图片描述

在这里插入图片描述

拓扑排序：0,2，5,1,3,4,6,7,8,9
etv:顶点的最早发生时间
ltv:顶点的最晚发生时间

节点的etv=ltv,就是图的关键路径；

1、计算etv[0-9] etv[0]的值为0；etv[2]的值为4；etv[5]的值为4+7=11；etv[1]的值为3；etv[3]的值为3+5=8与4+8=12之间选择，选择最大的为12；
etv[4]的值为3+6=9与12+3=15之间选择，选择最大的为15；
etv[6]的值为15+9=24；etv[7]的值为15+4=19与11+6=17之间选择，选择最大的19；etv[8]=19+5=24;etv[9]=24+3=27与24+2=26之间选择最大的；

if(temp->weight+etv[cur]>etv[temp->arcVertex])
{
etv[temp->arcVertex]=temp->weight+etv[cur];
}

2、计算ltv[0-9] ltv的计算采用拓扑排序结果的倒序，先初始化ltv[0-9]的值为etv[9]的值27，ltv[8]=ltv[9]-3=24; ltv[7]=ltv[8]-5=19; ltv[6]=ltv[9]-2=25;
ltv[4]有两条弧线（4-6）（4-7） ltv[7]-4=15 ltv[6]-9=16 选择最小的15
ltv[3]=15-3=12; ltv[1]也有两条，选址最小的ltv[3]-5=7; ltv[5]=ltv[7]-6=13;
ltv[2]也有两条，选择最小的ltv[3]-8=4; ltv[0]两条选择最小的ltv[2]-4=0;

etv[1]=3,ltv[1]=7 表明v1的事情从第七天开始做，也不会影响工程的进度。因为v0->v3要12天，v0->v1->v3只要保证12天完成，v1->v3是5天，所以v0->v1最大可以是7天。

程序
main.cpp


#include<iostream>
#include<stdio.h>
#include <stdlib.h>
#include<string>
#include"structfun.h"

using std::string;
using std::printf;
using std::scanf;
using std::endl;
using std::to_string;

void main()
{
//图的邻接矩阵
//AdjMarGraph amg;
//CreateAdjMaxGraph(&amg);//创建图的邻接矩阵
AdjMarDepthFirstSearch(&amg,0);//图的邻接矩阵深度优先遍历
 AdjMarBreadthFirstSearch(&amg);//广度优先遍历（递归）
// //AMBFS(&amg);//（非递归）
AdjMarGraphLeastPath(&amg);//图-最小生成路径（采用邻接矩阵）prim算法
printf("\n");
AdjMarGraphLeastPathKruskal(&amg);//图-最小生成路径（采用邻接矩阵）kruskal算法
//ShortestPath(&amg,9,0);//自己写的

//
//pathmatirx *p;
//shortpathtable *D;
//p=(pathmatirx*)malloc(sizeof(pathmatirx));
//D=(shortpathtable*)malloc(sizeof(shortpathtable));

//shortestpathA(&amg,4,p,D);//教科书上的

//shortestpathFloyd(&amg,0,9);//Floyd最短路径弗洛伊德算法



//图的邻接表
AdjListGraph alg;
CreateAdjListGraph(&alg);
TopologicalSort(&alg);//直接调用定点删除函数的方法
//TopologicalSortA(&alg);//拓扑排序
CriticalPath(&alg);//图邻接表-关键路径查找


//printf("删除的定点是：%s",DeleteAdjListVertex(&alg,0).c_str());
//AdjListDepthFirstSearch(&alg,0);//图的深度遍历
//AdjListBreadthFirstSearch(&alg);//图的广度遍历


//图的十字链表
//OrthogonalListGraph olg;
//CreateOrthogonalListGraph(&olg);

//图的邻接多重表
//AdjacencyMultipleTableGraph amtg;
//CreateAdjacencyMultipleTableGraph(&amtg);

system("pause");
}

structfun.h

//数据结构函数头文件

#include <stdio.h>
#include <iostream>
#include<string>

using std::cout;
using std::cin;
using std::string;

#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define INFINITY 6430//无穷大
typedef string ElemType;
typedef string VertexType;//图顶点数据类型
typedef int EdgeType;//图边的数据类型

//定义一个数组队列
typedef struct Queue
{
int date[MAXSIZE];
int num;
};

typedef struct stack{
	ElemType data[MAXSIZE];
	int top;
}stackList;

//初始化栈
int InitStack(stackList *L);

//入栈push
int push(stackList *L,ElemType e);

//出栈pop
ElemType pop(stackList *L);

//数据结构-图-----------------------------------------------------------------------------

//1、邻接矩阵（Adjacency Martix）
	//设置一个顶点数组vertex[],设置一个边数组arc[][]
typedef struct
{
	//图顶点数组
	VertexType vertex[MAXSIZE];
	//图边数组
	EdgeType arc[MAXSIZE][MAXSIZE];	//边的值就是权重
	int vertexnum,arcnum;
}AdjMarGraph;

//2、邻接表（Adjacency List）
	//设置一个顶点数组vertex[],设置一个边的链表，顶点的next指向所对应的链表

typedef struct EdgeNode//边链表节点
{
	EdgeType arcVertex;
	int weight;//权值
	EdgeNode *next;
}EdgeNode;

typedef struct//顶点数组
{
	VertexType vertex;
	EdgeNode *firstEdge;
	int in;//入度
}VertexList[MAXSIZE];

typedef struct//图结构
{
	VertexList vlist;
	int numVertex,numArc;

}AdjListGraph;

//3、十字链表（Orthogonal->正交的 List）
	//设置一个顶点数组vertex[],设置一个边的链表，顶点的next指向所对应的链表

//链表节点 tailvex headvex headlink,taillink; 改成invex,outvex,outlink,inlink更好理解
                                                //入顶点，出顶点，出链接，入链接
typedef struct OrthogonalLinkNode
{
	EdgeType invex,outvex;
	OrthogonalLinkNode *outlink,*inlink;
	int weight;//边的权重
}OrthogonalLinkNode;

//数组顶点节点 vertex 顶点 edgein 入边 edgeout 出边
typedef struct
{
	VertexType vertex;
	OrthogonalLinkNode *edgein,*edgeout;
}OrthogonalEdgeNode[MAXSIZE];

//十字链表结构
typedef struct 
{
	OrthogonalEdgeNode vertexlist;
	int numvertex,numedge;
}OrthogonalListGraph;

//4、无向图 邻接多重表结构Adjacency Multiple Table（邻接多重表就是一个顶点的多条边用链表链接）
//ivex ilink jvex jlink (ivex jvex 边的两个顶点，ilink指向值与ivex相同的jvex的节点,jlink指向值与jvex相同的下一个节点。

typedef struct AMTEdgeNode//边链表节点
{
	VertexType iver,jver;
	bool visited;//是否被访问过
	int weight;//权值
	AMTEdgeNode *ilink,*jlink;
}AMTEdgeNode;

typedef struct//顶点数组
{
	VertexType vertex;
	AMTEdgeNode *firstEdge;
}AMTVertexList[MAXSIZE];

typedef struct//图结构
{
	AMTVertexList vlist;
	int numVertex,numArc;

}AdjacencyMultipleTableGraph;

//5、图的边集数组
typedef struct
{
	int begin;//开始定点下标
	int end;//结束顶点下标
	int w;//权重
}EdgeArray[MAXSIZE];




//1、邻接矩阵
	//无向图的邻接矩阵
int CreateAdjMaxGraph(AdjMarGraph *amg);
int AdjMarDepthFirstSearch(AdjMarGraph *amg,int f);//邻接矩阵深度遍历 int f为开始的结点
int AdjMarBreadthFirstSearch(AdjMarGraph *amg);
int AMBFS(AdjMarGraph *amg);
//图-最小生成路径（采用邻接矩阵）
int AdjMarGraphLeastPath(AdjMarGraph *amg);//prim算法
int AdjMarGraphLeastPathKruskal(AdjMarGraph *amg);//Kruskal算法

//图-两个顶点之间的最小路径（ShortestPath）
int ShortestPath(AdjMarGraph *amg,int begin,int end);
#define MAXVER 9
typedef int pathmatirx[MAXVER];
typedef int shortpathtable[MAXVER];
void shortestpathA(AdjMarGraph *amg,int v0,pathmatirx *p,shortpathtable *D);
void shortestpathFloyd(AdjMarGraph *amg,int begin,int end);


//2、邻接表
int CreateAdjListGraph(AdjListGraph *alg);
string DeleteAdjListVertex(AdjListGraph *alg,int vertexcur);//删除顶点
void TopologicalSort(AdjListGraph *alg);//拓扑排序直接删除定点
void TopologicalSortA(AdjListGraph *alg,stackList *stack1,int *etv[MAXSIZE],int *ltv[MAXSIZE]);//拓扑排序改变入度
void CriticalPath(AdjListGraph *alg);//图邻接表-关键路径查找
int AdjListDepthFirstSearch(AdjListGraph *alg,int f);//邻接表深度遍历
int AdjListBreadthFirstSearch(AdjListGraph *alg);//邻接表广度遍历

structfun.cpp

#include<iostream>
#include<stdio.h>
#include<string>
#include<sstream>
#include"structfun.h"


using std::cout;
using std::cin;
using std::string;
using std::endl;
using std::ostringstream;
using std::stoi;
using std::to_string;
//初始化栈
int InitStack(stackList *L)
{
	for(int i=0;i<MAXSIZE;i++)
		(*L).data[i]="";
	(*L).top=-1;
	return 1;
}

//入栈push
int push(stackList *L,ElemType e)
{
	//
	if((*L).top>MAXSIZE)
		return 0;
	(*L).top=(*L).top+1;
	(*L).data[(*L).top]=e;
	return 1;
}

//出栈pop
ElemType pop(stackList *L)
{
	ElemType e;
	if((*L).top==-1)
		return 0;
	e=(*L).data[(*L).top].c_str();
	(*L).data[(*L).top]="";
	(*L).top=(*L).top-1;
	return e;
}

int CreateAdjListGraph(AdjListGraph *alg)
{
	int i=0;
	alg->numVertex=0;
	alg->numArc=0;
	FILE *fp=fopen("4.txt","rb");//文件使用方式由r,w,a,t,b，+各字符的含义是：r(read): 只读 w(write): 只写 a(append): 追加 t(text): 文本文件，可省略不写 b(binary): 二进制文件 +: 读和写
	while(1)//创建顶点
	{
		printf("请输入邻接表的顶点结束用#：");
		fscanf(fp,"%s",alg->vlist[i].vertex.c_str());
		printf("%s\n",alg->vlist[i].vertex.c_str());
		//cin>>alg->vlist[i].vertex;
		if(*alg->vlist[i].vertex.c_str()=='#')
			break;
		alg->vlist[i].firstEdge=NULL;
		alg->vlist[i].in=0;//初始化入度为0
		i++;
		alg->numVertex++;

	}
		while(1)//创建边链表
	{
		int v1=0,v2=0,w=0;
		EdgeNode *edgenode;
		printf("请输入邻接表的顶点对应的边（v1,v2,w）以(0,0,0)结束：");
		fscanf(fp,"%d,%d,%d",&v1,&v2,&w);
		printf("%d,%d,%d\n",v1,v2,w);

		if(!v1&&!v2&&!w)//(0,0,0)结束
			break;

		alg->vlist[v2].in++;//目的边的入度加1

		edgenode = new EdgeNode();//创建边节点
		edgenode->arcVertex=v2;
		edgenode->weight=w;
		edgenode->next=NULL;

		if(alg->vlist[v1].firstEdge==NULL)//插入边节点
			alg->vlist[v1].firstEdge=edgenode;
		else
		{
			EdgeNode *temp;
			temp=alg->vlist[v1].firstEdge;

			while(temp->next!=NULL)
				temp=temp->next;
			temp->next=edgenode;
		}

		//无向图要添加反方向的边，跟上面的代码一样，只是v1换成v2 v2换成v1
		/*edgenode = new EdgeNode();//创建边节点
		edgenode->arcVertex=v1;
		edgenode->weight=w;
		edgenode->next=NULL;

		if(alg->vlist[v2].firstEdge==NULL)//插入边节点
			alg->vlist[v2].firstEdge=edgenode;
		else
		{
			EdgeNode *temp;
			temp=alg->vlist[v2].firstEdge;

			while(temp->next!=NULL)
				temp=temp->next;
			temp->next=edgenode;
		}

		alg->numArc++;*/
	}
		return OK;
}
//删除邻接表定点,传入要删除定点的下标，返回成功该定点；
string DeleteAdjListVertex(AdjListGraph *alg,int vertexcur)
{
	string str;
	str=alg->vlist[vertexcur].vertex.c_str();

	//处理入度减1
	EdgeNode *temp;
	temp=alg->vlist[vertexcur].firstEdge;
	while(temp)
	{
		alg->vlist[temp->arcVertex].in--;//减入度
		alg->numArc--;//减边数
		temp=temp->next;
	}

	if(vertexcur<0&&vertexcur>alg->numVertex)
		return 0;
	alg->vlist[vertexcur].firstEdge=NULL;
	int vertexcur1=vertexcur;
	while(vertexcur<alg->numVertex) //删除顶点
	{
		alg->vlist[vertexcur].vertex=alg->vlist[vertexcur+1].vertex.c_str();
		alg->vlist[vertexcur].firstEdge=alg->vlist[vertexcur+1].firstEdge;
		alg->vlist[vertexcur].in=alg->vlist[vertexcur+1].in;
		
		vertexcur++;
	}

	alg->numVertex--;//定点数减1

		//所有边链表下标减1
	for(int i=0;i<alg->numVertex;i++)
	{
		temp=alg->vlist[i].firstEdge;
		while(temp)
		{
			if(temp->arcVertex>=vertexcur1)
			{temp->arcVertex--;}
			temp=temp->next;
		}
	}
	
	return str;

}
//拓扑排序
void TopologicalSort(AdjListGraph *alg)
{
//定义一个栈，存储入度为零的定点
	stackList stack;
	InitStack(&stack);
	string vc;
	int count=0,vnum=alg->numVertex;
	

	while(1)//判断入度是否为零，为零删除定点
	{
		for(int i=0;i<alg->numVertex;i++)
		{
			if(alg->vlist[i].in==0)
			{
			push(&stack,alg->vlist[i].vertex.c_str());
			printf("%s->",alg->vlist[i].vertex.c_str());//打印被删除的定点
			DeleteAdjListVertex(alg,i);
			count++;
			i--;
			}
		}
		
		vc=pop(&stack).c_str();

		//printf("%s->",vc.c_str());
		if(stack.top==-1)
		{
			if(count==vnum)
				printf("AOV网不存在环");
			else
				printf("AOV网存在环");
			break;
		}
	
	}
}

void TopologicalSortA(AdjListGraph *alg,stackList *stack1,int etv[],int ltv[])
{
	//定义一个数组
	stackList stack;
	InitStack(&stack);
	InitStack(stack1);
	int count=0,i,max=0,min;

	//查找入度为零的定点
	for(i=0;i<alg->numVertex;i++)
	{

		if(alg->vlist[i].in==0)
		{
			push(&stack,to_string((long long)i));//入度为零的顶点下标入栈
		}
	}

	//处理并打印
	while(stack.top!=-1)
	{
		
		string vstr;
		int cur;
		EdgeNode *temp;
		temp=(EdgeNode*)malloc(sizeof(EdgeNode));
		vstr=pop(&stack);
		cur=stoi(vstr.c_str());
		printf("%s->",alg->vlist[cur].vertex.c_str());
		push(stack1,to_string((long long)cur));//排序结果存入栈2，用于计算ltv,ltv采用倒序，符合栈的特点
		                                            //9,8,7,6,4,3,1,5,2,0

		count++;
		//遍历该定点连接的其他边，把他们的入度减一
		temp=alg->vlist[cur].firstEdge;
		//etv[cur]=max;
		while(temp!=NULL)
		{
			if(temp->weight+etv[cur]>etv[temp->arcVertex])//选择较大的etv值存入etv数组。用于查找关键路径
			{
				etv[temp->arcVertex]=temp->weight+etv[cur];
			}
			//temp->weight>etv[cur]?etv[cur]=max+temp->weight:etv[cur];
			if(!--alg->vlist[temp->arcVertex].in)
				push(&stack,to_string((long long)temp->arcVertex));//入度为零的顶点下标入栈
			temp=temp->next;	
		}
		
	}
	//计算数组ltv值，倒序从定点9开始
	
	for(int i=0;i<alg->numVertex;i++)//初始化ltv为最后一个定点的etv
		ltv[i]=etv[alg->numVertex-1];

		while(stack1->top!=-1)
		{
		int	cur=stoi(pop(stack1).c_str());//栈2中取出顶点下标

		EdgeNode *temp;
		temp=(EdgeNode*)malloc(sizeof(EdgeNode));
		temp=alg->vlist[cur].firstEdge;

		while(temp!=NULL)//循环遍历顶点所连接的边
		{
			if(ltv[temp->arcVertex]-temp->weight<ltv[cur])//选择较小的etv值存入ltv数组。用于查找关键路径
			{
				ltv[cur]=ltv[temp->arcVertex]-temp->weight;
			}
			temp=temp->next;
		}

		}

	if(count==alg->numVertex)
		printf("AOV网不存在环");
	else
		printf("AOV网存在环");

}

//图邻接表-关键路径查找
void CriticalPath(AdjListGraph *alg)
{
	int etv[MAXSIZE],ltv[MAXSIZE];//定义顶点最早发生时间etv,最晚发生时间ltv
	int ete=0,lte=0,max,min;//定义最早开工时间ete，最晚开工时间lte

	for(int i=0;i<alg->numVertex;i++)//初始化
	{
		etv[i]=ltv[i]=0;
	}

	stackList stack1;
	TopologicalSortA(alg,&stack1,etv,ltv);//拓扑排序，并计算出etv,ltv
	//输出关键路径
	printf("\n工程的关键路径为：");
	for(int i=0;i<alg->numVertex;i++)
		if(ltv[i]==etv[i])
			printf("->%s",alg->vlist[i].vertex.c_str());


}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值