《深度学习入门-基于Python的理论与实现》第七章带读 -- CNN介绍

《深度学习入门-基于Python的理论与实现》第七章带读 – CNN介绍

• 开篇介绍：《深度学习入门-基于Python的理论与实现》书籍介绍
• 第一章：《深度学习入门-基于Python的理论与实现》第一章带读
• 第二章：《深度学习入门-基于Python的理论与实现》第二章带读 – 感知机
• 第三章：深度学习入门-基于Python的理论与实现》第三章带读 – 神经网络
• 第四章：《深度学习入门-基于Python的理论与实现》第四章带读 – 神经网络的学习
• 第五章：《深度学习入门-基于Python的理论与实现》第五章带读 – 误差反向传播
• 第六章：《深度学习入门-基于Python的理论与实现》第六章带读 – 训练方法介绍

---

在第六章，我们介绍了深度学习模型训练过程中非常重要的一些技巧，包含了：

• 如何更新模型的参数
• 如何初始化需要的权重
• Batch Normalization
• 正则化处理
• 超参数验证

本章，我们一起看看深度学习中非常重要的一个模型：卷积神经网络（Convolutional Neural Network，CNN） ，其被广泛用于图像识别、语音识别等领域。

7.1 整体结构

CNN网络在之前神经网络的基础上，增加了卷积层 （Convolution层）和池化层（Pooling层）。我们先来看看之前基于全连接层（Affine层）的神经网络图：

基于CNN的网络的例子:新增了Convolution层和Pooling层(用灰色的方块表示)：

对比发现，CNN中新增了 Convolution 层和 Pooling 层。CNN中层的连接顺序是“Convolution - ReLU - （ Pooling） ”（Pooling 层有时会被省略）。这可以理解为之前的“Affine - ReLU” 连接被替换成了“Convolution - ReLU - （ Pooling） ”连接。

除此之外，CNN中，靠近输出的层中使用了之前 的“Affine - ReLU” 组合。还有，最后的输出层中使用了之前的“Affine Softmax” 组合。

7.2 卷积层

a.全连接层存在的问题

问题：数据的形状被“忽视”了。

如：前面提到的使用了 MNIST 数据集的例子中，输入图像就是 1 通道、高 28 像素、长 28 像素 的（1, 28, 28）形状，但却被排成1列，以784个数据的形式输入到最开始的 Affine层。

基于以上问题，我们需要找出一种方法，既可以学习到需要的特征，又保持形状相关的信息。而卷积层就可以满足这个需求。

接下来，我们看看卷积层是如何进行运算的。

b.卷积运算

卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的“滤波器运算”。

卷积层运算结果：

计算过程：

通过，最后内容 = 矩阵对应位置*滤波器

15 =

12+20+31+00+11+22+31+00+1*2 =

2+3+1+4+3+2

最后在上内容中增加偏置：

c.填充

在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比如0等），这称为填充（padding），是卷积运算中经常会用到的处理。

卷积运算的填充处理如下图:向输入数据的周围填入0(图中用虚线表示填充,并省略了填充的内容"0”)

为什么要进行padding呢？

使用填充主要是为了调整输出的大小。比如，对大小为(4, 4)的输入数据应用(3, 3)的滤波器时，输出大小变为(2, 2)，相当于输出大小 比输入大小缩小了2个元素。这在反复进行多次卷积运算的深度网络中会成为问题。

为什么呢？因为如果每次进行卷积运算都会缩小空间，那么在某个时刻输出大小就有可能变为1，导致无法再应用卷积运算。为了避免出现这样的情况，就要使用填充。在刚才的例子中，将填充的幅度设为1，那么相对于输入大小(4, 4)， 输出大小也保持为原来的(4, 4)。因此，卷积运算就可以在保持空间大小不变的情况下将数据传给下一层。

d.步幅

应用滤波器的位置间隔称为步幅（stride）。之前的例子中步幅都是1，如果将步幅设为2，则如图所示，应用滤波器的窗口的间隔变为2个元素。

根据之前观察，我们发现：增大步幅后，输出大小会变小。而增大填充后，输出大小会变大。

具体他们之间会有什么关系呢？

假设输入大小为(H, W)，滤波器大小为(FH, FW)，输出大小为 (OH, OW)，填充为P，步幅为S。此时，输出大小可通过式(7.1)进行计算。

e.三维数组的卷积运算

之前卷积运算的例子都是以有高、长方向的2维形状为对象的。但是，图像是3维数据，除了高、长方向之外，还需要处理通道方向（一般黑白图片为1通道，彩色图片为3通道）。

3通道数据计算结果：

3通道数据计算过程：

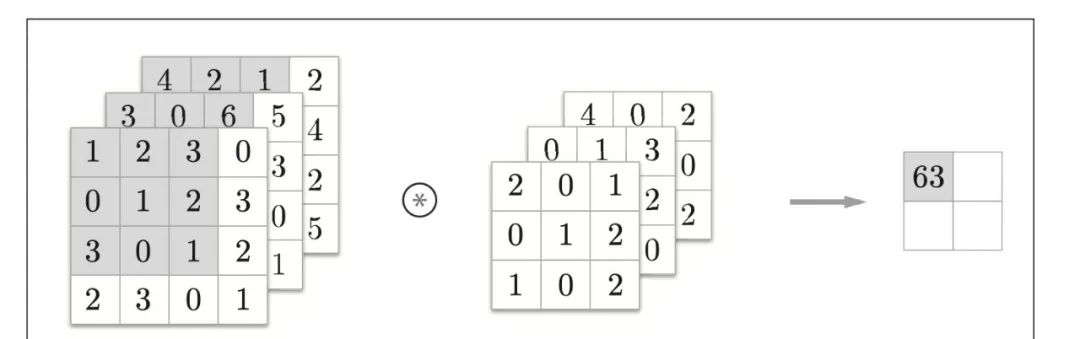
通过每个通道分别计算，最后进行求和。

7.3 池化层

a.池化层的介绍

池化层的目的是：缩小高、长方向上的空间的运算。

一般有最大池化和平均池化。

• 最大池化：从目标区域中取出最大值
• 平均池化：计算目标区域的平均值

举例：按照步幅2进行2*2的最大池化处理顺序：

b.池化层的特征

• 没有要学习的参数

• • 池化只是从目标区域中取最大值（或者平均值），所以不存在要学习的参数。

• 通道数不发生变化

• • 经过池化运算，输入数据和输出数据的通道数不会发生变化。计算是按通道独立进行的。
    • 

• 对微小的位置变化具有鲁棒性（健壮）

• • 输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对输入数据的微小偏差具有鲁棒性。

7.4 具有代表性的CNN网络

前面我们介绍了CNN中的卷积层和池化层，其实如果堆叠了多层卷积层，则随着层次加深，提取的信息也愈加复杂、抽象，这是深度学习中很有意思的一个地方。最开始的层对简单的边缘有响应，接下来的层对纹理有响应，再后面的层对更加复杂的物体部件有响应。也就是说，随着层次加深，神经元从简单的形状向“高级”信息变化。换句话说，就像我们理解东西的“含义”一样，响应的对象在逐渐变化。

如下图：CNN的卷积层中提取的信息。第1层的神经元对边缘或斑块有响应,第3层对纹理有响应,第5层对物体部件有响应,最后的全连接层对物体的类别(狗或车)有响应。

关于CNN，迄今为止已经提出了各种网络结构。这里，我们介绍其中特别重要的两个网络，一个是在1998年首次被提出的CNN元祖LeNet ， 另一个是在深度学习受到关注的2012年被提出的AlexNet。

a.LeNet

LeNet在1998年被提出，是进行手写数字识别的网络。如下图，它有连续的卷积层和池化层（正确地讲，是只“抽选元素”的子采样层），最后经全连接层输出结果。

和“现在的CNN”相比， LeNet有几个不同点。

• 第一个不同点在于激活函数。LeNet 中使用sigmoid 函数，而现在的 CNN 中主要使用 ReLU 函数。
• 此外，原始的LeNet中使用子采样（subsampling）缩小中间数据的大小，而 现在的CNN中Max池化是主流。

b.AlexNet

AlexNet是引发深度学习热潮的导火线，不过它的网络结构和LeNet基本上没有什么不同.

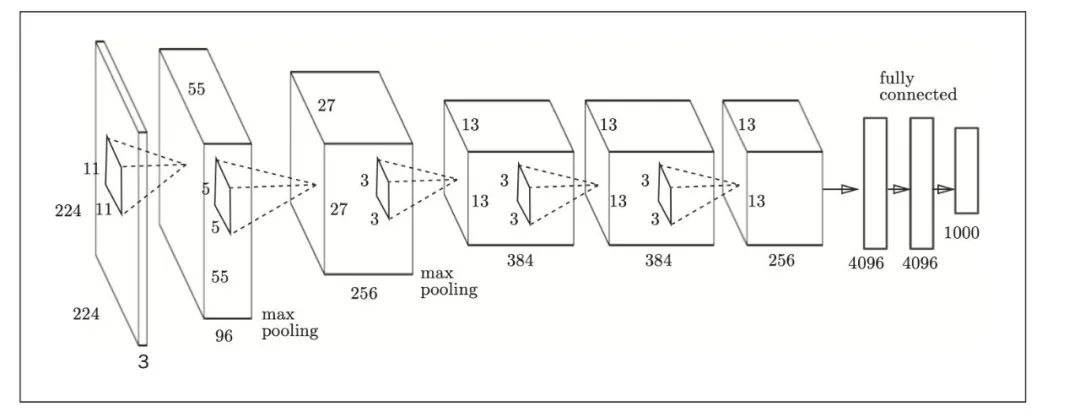
AlexNet叠有多个卷积层和池化层，最后经由全连接层输出结果。虽然结构上AlexNet和LeNet没有大的不同，但有以下几点差异:

• 激活函数使用ReLU。
• 使用进行局部正规化的LRN（Local Response Normalization）层。
• 使用Dropout。

7.5 小结

这一章中主要介绍了CNN，以及卷积层和池化层。同时我们在其基础上又介绍了LeNet和AlexNet两个网络。本章中的难点是卷积层和池化层的理解。

---

---

书籍下载链接：https://pan.baidu.com/s/1goHhf2GZt0gxxbLXa42CmA
密码: 4vi2

---

欢迎微信搜索关注微信公众号【布道NLP】获取更多AI相关资料和知识。