[Leetcode]python3算法攻略（优先队列/双端队列）

1.知识点

优先队列：





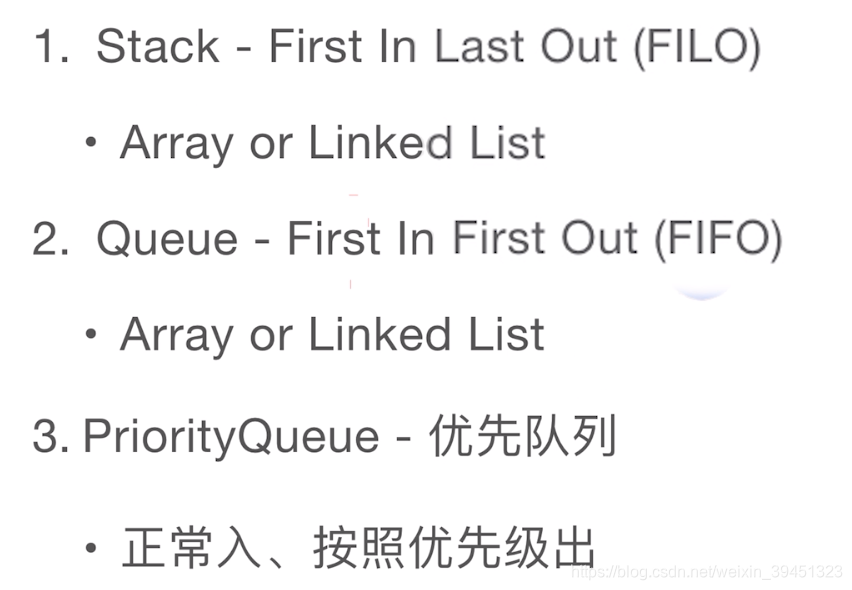
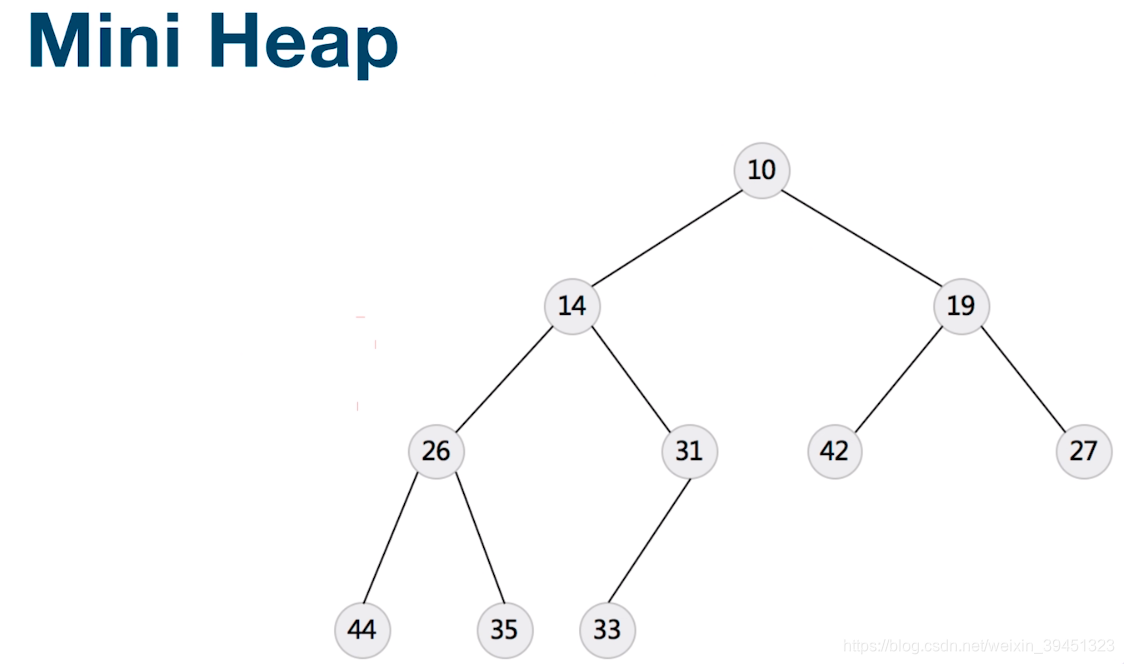
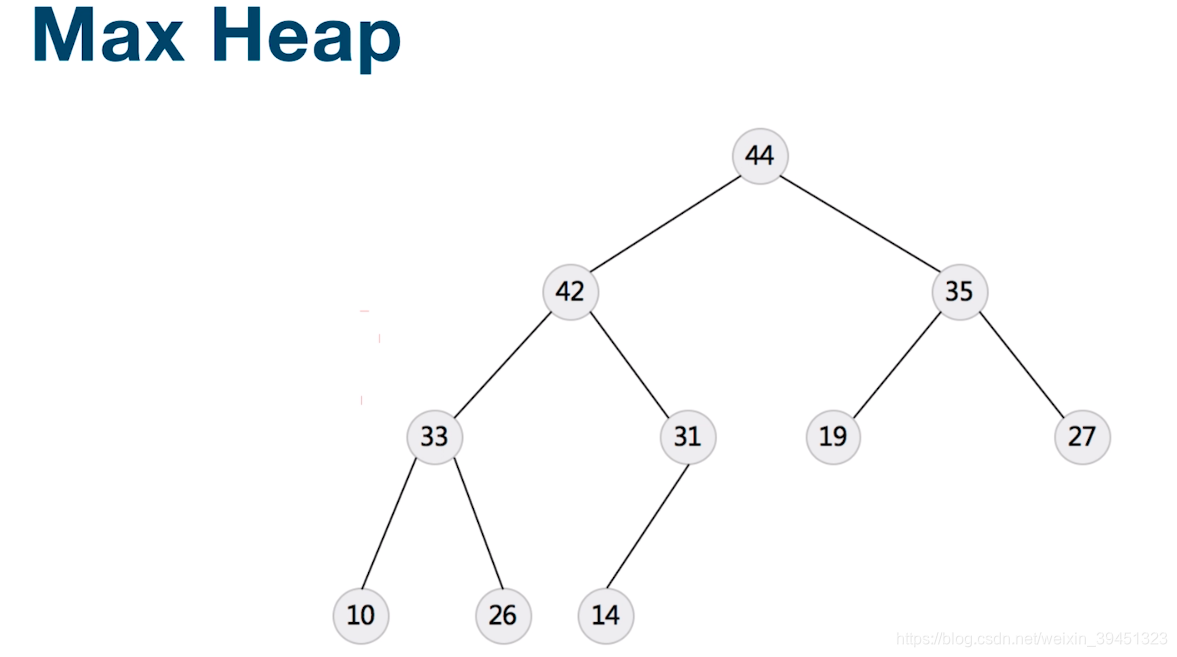
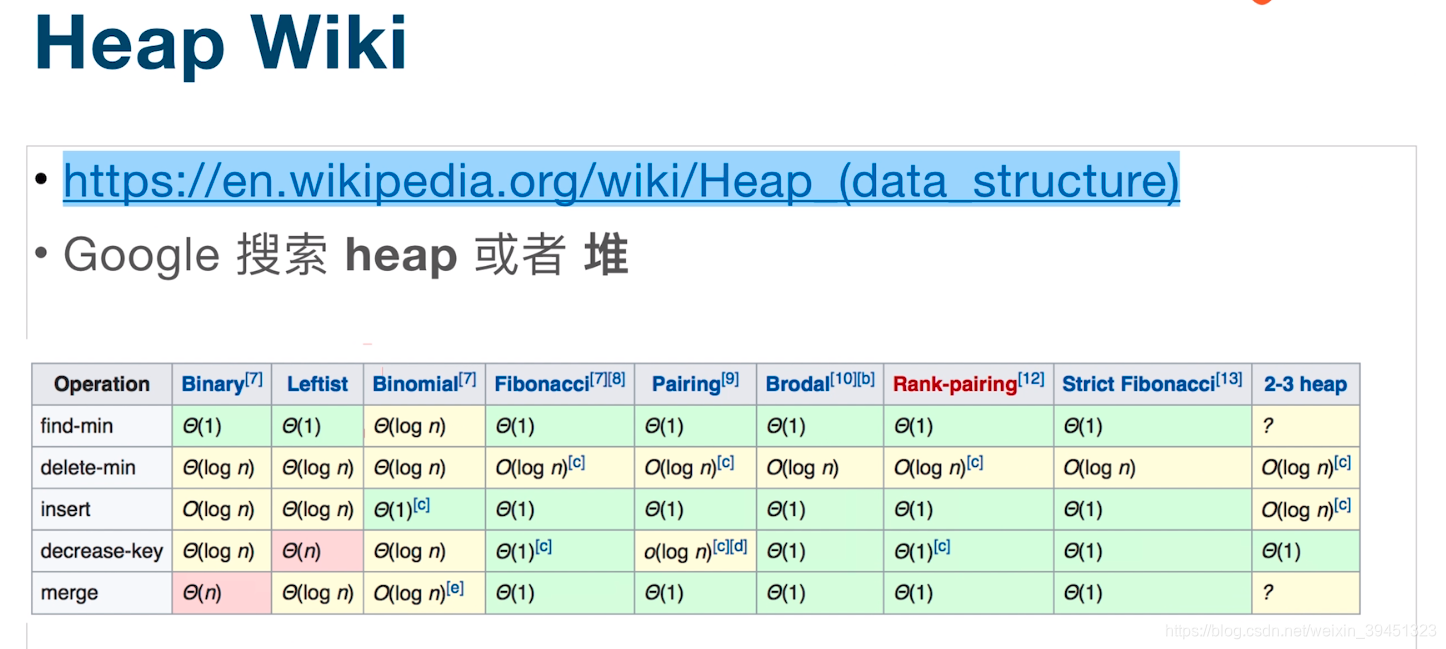
特点：

和队列基本操作相同:

top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾 (并排序)
emplace 原地构造一个元素并插入队列
pop 弹出队头元素
swap 交换内容

2 代码实战

2.1 代码demo理解Priority-Queue

• 优先输出大数据
  priority_queue<Type, Container, Functional>
  • Type为数据类型，Container为保存数据的容器，Functional为元素比较方式。

如果不写后两个参数，那么容器默认用的是vector，比较方式默认用operator，也就是优先队列是大顶堆，队头元素最大。
eg：

#include<iostream>
#include<queue>
using namespace std;
 
int main(){
	priority_queue<int> p;
	p.push(1);
	p.push(2);
	p.push(8);
	p.push(5);
	p.push(43);
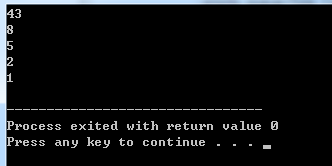
	for(int i=0;i<5;i++){
		cout<<p.top()<<endl;
		p.pop();
	}
	return 0;
}

结果：

• 优先输出小数据
  • priority_queue<int, vector, greater > p;

#include<iostream>
#include<queue>
using namespace std;

int main(){
   priority_queue<int, vector<int>, greater<int> >p;
   p.push(1);
   p.push(2);
   p.push(8);
   p.push(5);
   p.push(43);
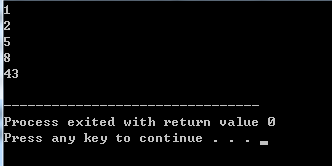
   for(int i=0;i<5;i++){
   	cout<<p.top()<<endl;
   	p.pop();
   }
   return 0;
}

2.2 Kth Largest Element in a Stream

703. Kth Largest Element in a Stream


利用优先队列中，最小堆的算法，可将时间复杂度降低。上图所示，k*log(k)是快排的时间复杂度，log（2）k是Min Heap的时间复杂度。
C++代码：

class KthLargest {
public:
    KthLargest(int k, vector<int>& nums) {
        int i;
        kth = k;
        //将arr中前k个数据放入优先队列中，排序，最小的数在队头
        for ( i = 0; i < k && i < nums.size(); i++ )
            q.push(nums[i]);
        //维护具有k个元素的小顶堆.
        while(i < nums.size()) {
            if (nums[i] > q.top() ) {
                q.pop();
                q.push(nums[i]);
            }
            i++;
        }
    }
    
    int add(int val) {
        int k;
        //如果堆为空或者堆长小于k，则继续向堆中加入数据
        if (q.empty() || q.size() < kth ) {
            q.push(val);
        } else {
            k = q.top();          //找到堆顶元素，即堆中最小的数
            if (val > k ) {       //和实时传来的数做比较，维护小顶堆
                q.pop();
                q.push(val);
            }
        }
        return q.top();     //如果传过来的数比推顶的数小，则舍弃，返回原堆顶的数即可
    }
    private :
        priority_queue<int,vector<int>,greater<int>> q;
        int kth;
};
/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest* obj = new KthLargest(k, nums);
 * int param_1 = obj->add(val);
 */

2.3 Sliding Window Maximum

239. Sliding Window Maximum



此题中，不用优先队列。因为窗口中只要维护最大值即可，不用维护第二大，第三大的值，所以算法可以加速，采用双端队列的方法。

维护队列左边最大。

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        //判断输入是否合法
        if not nums : return []
        //初始化window和存放结果的列表
        window, res = [], []
        for i, x in enumerate(nums):
            //维护窗口大小为k
            if i >= k and window[0] <= i - k:
                window.pop(0)
            //将左侧比当前x值小的数据索引都清掉，维护左端最大
            while window and nums[window[-1]] <= x:
                window.pop()
            window.append(i)
            //将最大值放入res列表中
            if i >= k-1:
                res.append(nums[window[0]])
        return res