DBMS_index_and_storage（数据库第八章：索引与存储）

课本：
8.1 外部存储上的数据
磁盘上读取信息的单位是页（4or8KB）
页I/O代表了典型数据库操作代价（主存磁盘交互），需要优化

磁盘：允许固定的代价检索每一页。（按照页面存储的物理顺序连续读取<任意顺序读取相同页数）
磁带：顺序访问，不常用于数据的存档
文件中的每一个记录有唯一的标识符，rid。一个rid有一个属性，识别包含记录的页在磁盘的地址

缓冲区管理器的软件层完成数据与内存以及磁盘的交互
磁盘管理器管理磁盘的中文件使用的页

理解：

8.2 文件组织与索引
最简单的无序文件是无序文件，或称堆文件。一个堆文件中的数据在文件页中以任意的顺序排列。
索引为磁盘上组织记录数据的一种数据结构。方便查询。
理解为：索引可以有多个（类比select c1 c2…的条件查询）
数据项：存储在索引文件中的记录。键值为K的数据项记为K*。
索引的数据项存储：
数据项K*是一个真正的数据记录。
数据项是一个<k,rid>对，其中rid是搜索键值为K的数据记录的记录id。
数据项是一个<k,rid-list>对，其中rid-list是搜索键值为K,的数据记录的记录id列表。

聚簇索引
数据记录的顺序与某一索引的数据项顺序相同或类似，我们就称这类索引是聚簇索引。否则就是非聚簇索引。
一聚簇，二三非。

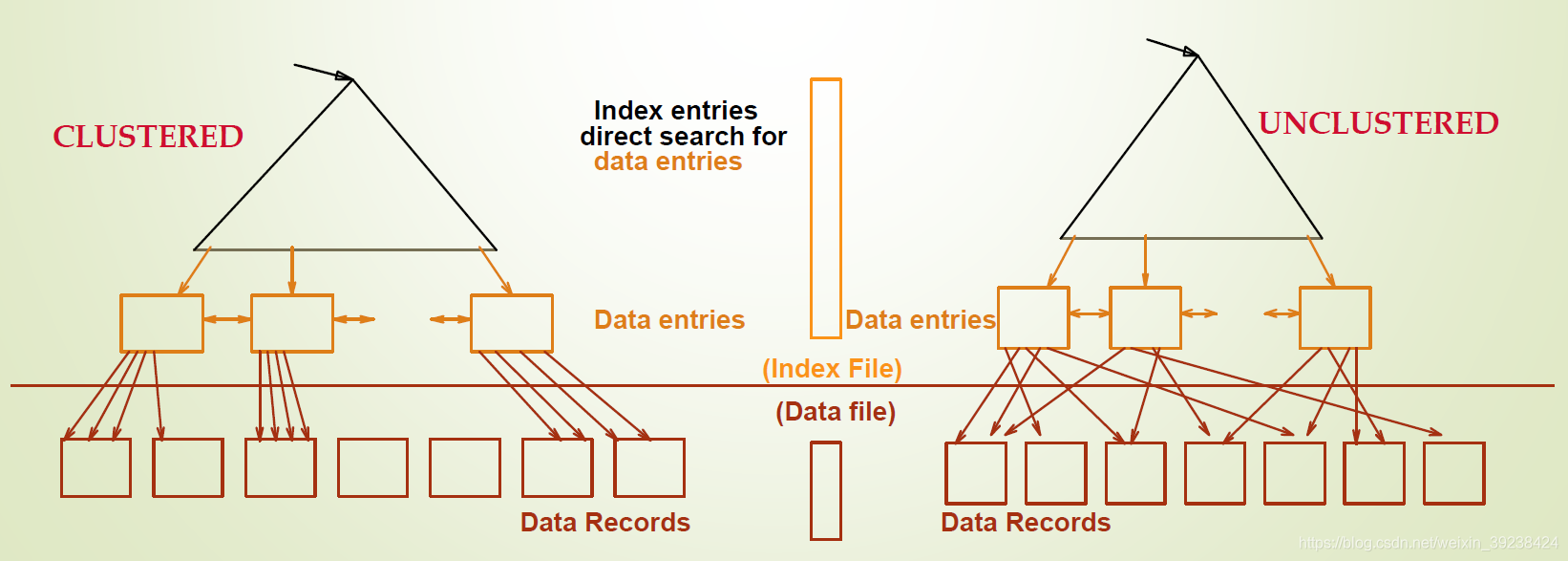
聚簇的只需要检索部分数据页即可。非聚簇的每一条都需要检索相应的数据页。

关于索引的一些重点：
聚簇索引一般就是主键索引，基于主键建立B+树的索引，使得基于主键查询速度更快；
非聚簇索引就是给普通字段加上B+树索引，存在重复的情况，但是相对不加索引的查询效率高很多，不加的话就是一条条查询
联合索引是由多个字段联合组成的，最左前缀原则：
（A, B, C）这样的索引组合 A AB ABC 这样的才走该索引（严格存在 只能等于 或者like %XXX 但是查询语句中可以顺序颠倒），如果只有一个字段A也是走这条索引，创建的时候就建立了 A AB ABC这样的索引结构；如果存在单键索引（比如单独 A 单独B 单独C）则存在查询优化选择 走联合索引还是单键索引，一般来说联合索引效率更高，但是只符合以A开头的情况
查询中存在 A and B的情况时，查询优化可能走一个或者两个单键索引， A or B的情况时则会走两个索引，如果其中一个没有索引的话，则不走索引。
索引的建立：不宜建立太多索引，会增加磁盘开销，同时增加磁盘更新的开销，对于少量数据做索引会降低效率。建立联合索引时，将最经常查询的数据放在最左边。

8.3 索引数据结构
组织数据项的方法之一是按照搜索码对数据项进行哈希。

基于哈希的索引

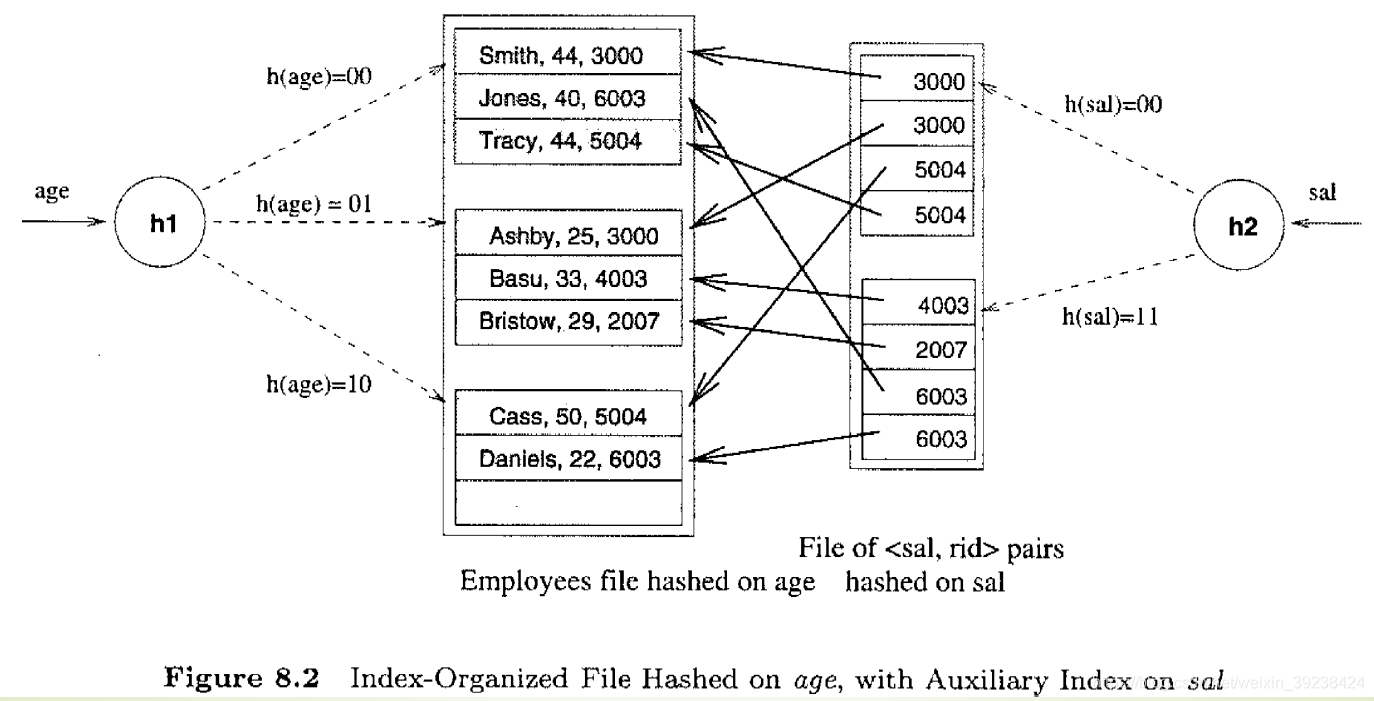
左边为第一个数据项，右边为第二个数据项（sal，rid）
但是文件是按照age进行hash排序的。

基于树的索引：

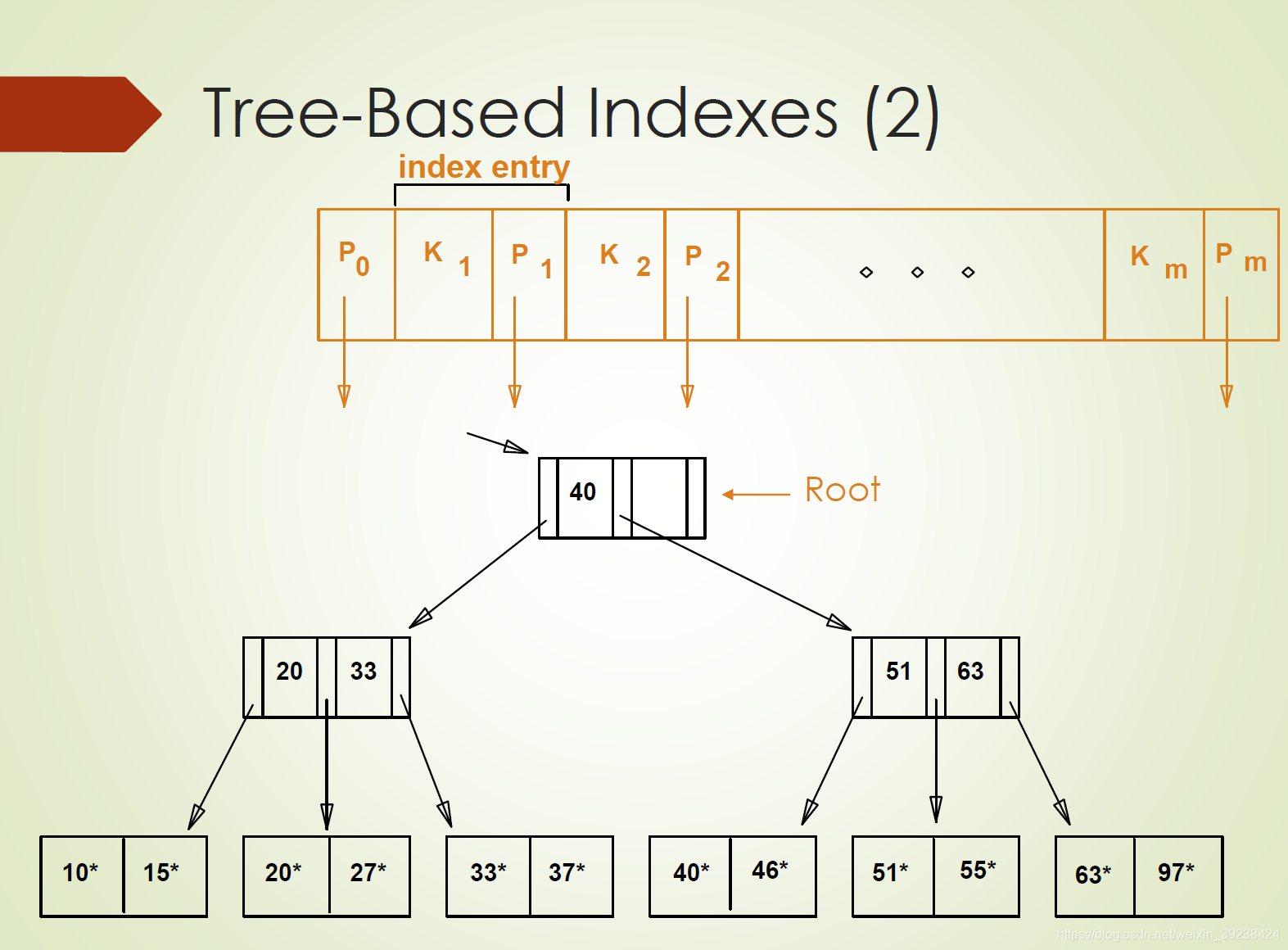
每一个节点是一个物理页，每检索一个节点就涉及一次I/O。
在搜索中出现的磁盘I/O数等于，从根节点到叶节点的路径加上满足条件的叶子页的个数。
上图中树的高度为3，而访问一个叶子页的I/O次数为4（其实一般根节点在缓冲池中，所以I/O次数为3）。

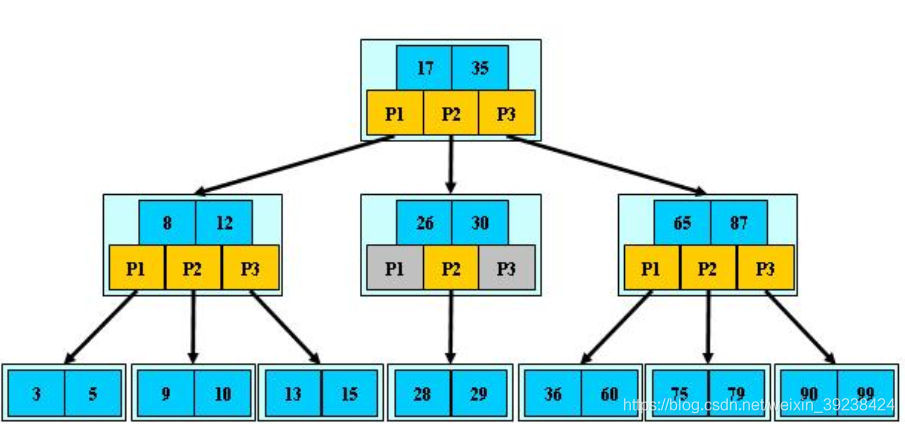
B树：
B树的定义

B树也称B-树,它是一颗多路平衡查找树。我们描述一颗B树时需要指定它的阶数，阶数表示了一个结点最多有多少个孩子结点，一般用字母m表示阶数。当m取2时，就是我们常见的二叉搜索树。

一颗m阶的B树定义如下：

1）每个结点最多有m-1个关键字。

2）根结点最少可以只有1个关键字。

3）非根结点至少有Math.ceil(m/2)-1个关键字。

4）每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。

5）所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。
6）根结点的儿子数为[2, M]；除根结点以外的非叶子结点的儿子数为[M/2, M]。
7）非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

B+树索引：

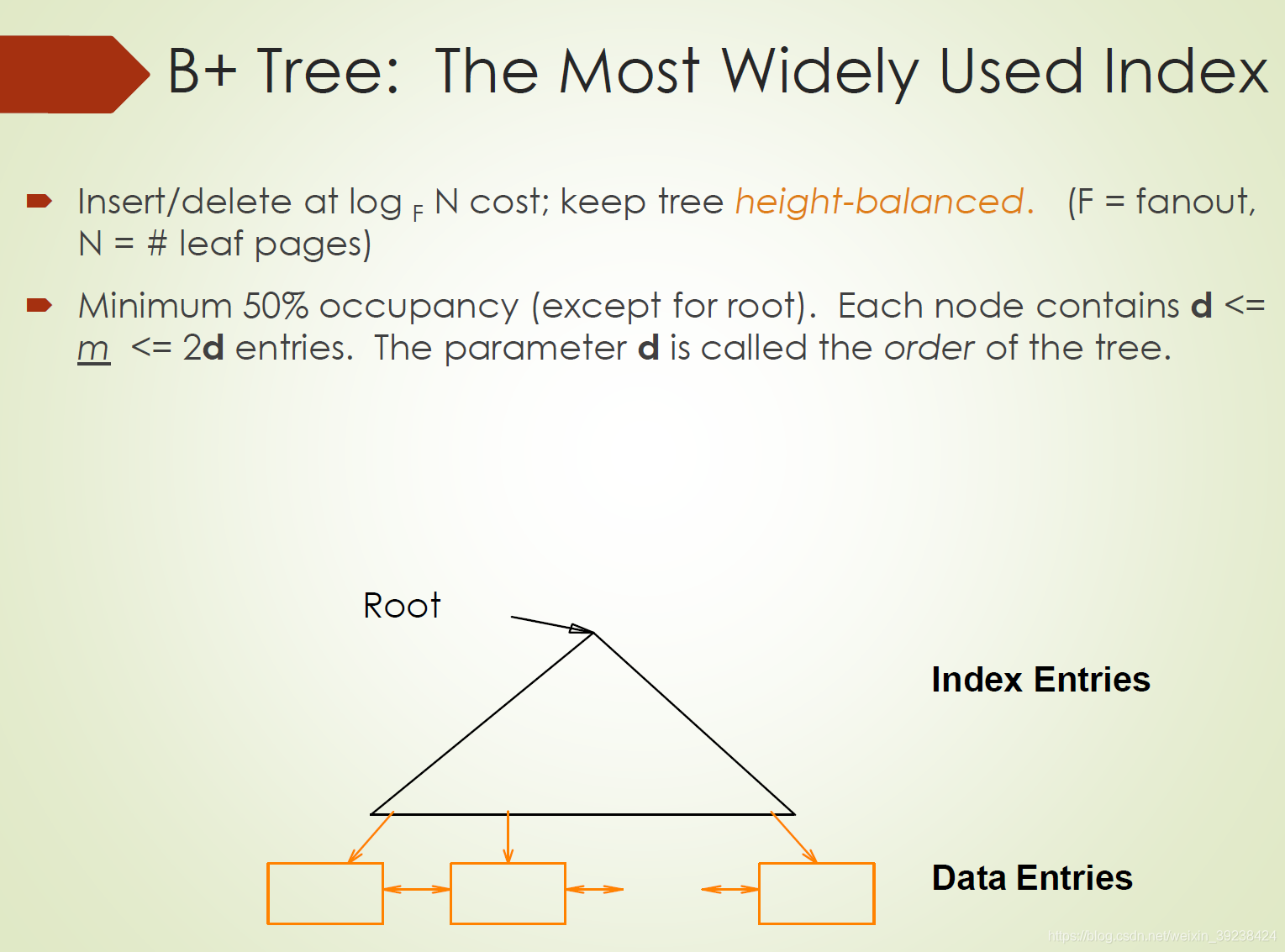
B+ 树是一种树数据结构，是一个n叉树，每个节点通常有多个孩子，一颗B+树包含根节点、内部节点和叶子节点。 B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。 B+ 树元素自底向上插入。
一个m阶（5）的B树具有如下几个特征（类似于B树）：
1.根结点至少有两个子女。
2.每个中间节点都至少包含ceil(m / 2)-1个孩子，最多有m-1个孩子（到5个元素，触发分裂操作）。
3.每一个叶子节点都包含k-1（2~4）个元素，其中 m/2 <= k <= m。
////////////////////////////上面也是B树的性质
3.非叶子结点的子树指针与关键字个数相同；
4.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树
（B-树是开区间）；
5.为所有叶子结点增加一个链指针；
6.所有关键字都在叶子结点出现；

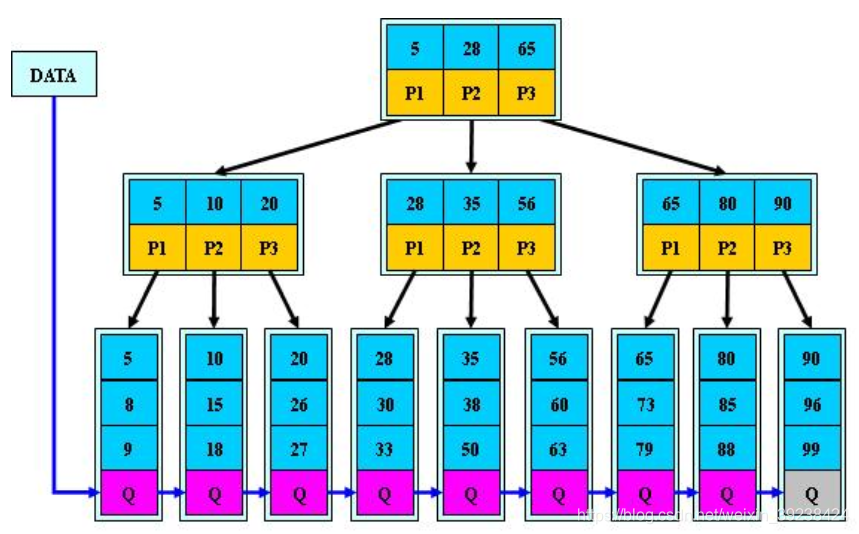
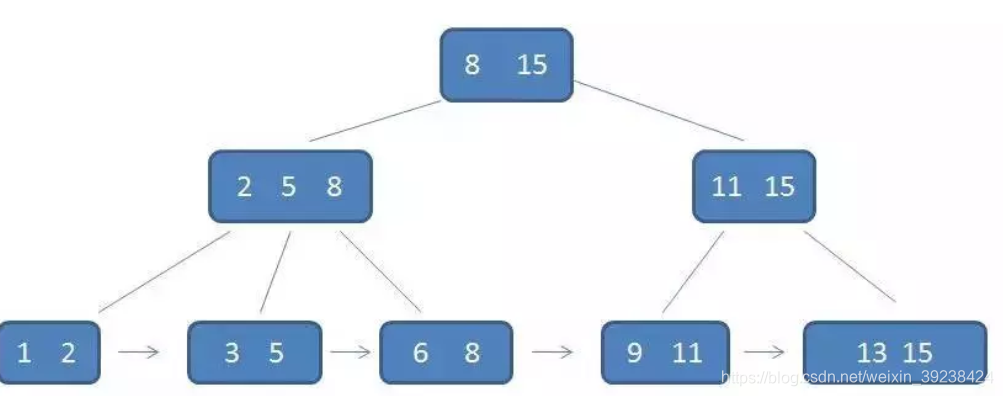
只有叶子节点才会有data，其他都是索引。

B+树与B树的区别
有k个子结点的结点必然有k个关键码；
非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。
树的所有叶结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

查询：
比起B树，B+树 ①IO次数更少 ②查询性能很稳定 ③范围查询更简便
B+树查询需要查到叶子节点

B+树的插入操作

1. 若为空树，那么创建一个节点并将记录插入其中，此时这个叶子结点也是根结点，插入操作结束。

2. 假设允许的最大节点元素个数为4

则在元素插入进来的时候，未满4个的直接插入即可

3. 一旦插入第五个值（插入排序后），需要进行分裂。左边(m-1)/2…2右边m-(m-1)/2…3。中间第三个元素成为索引节点的key（记录在父节点中）。右边孩子指针指向父节点。
   
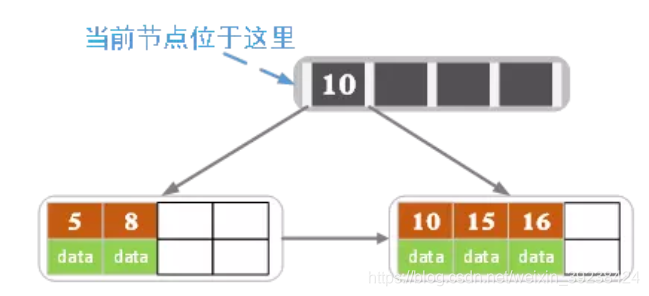
4. 不断插入后导致父节点索引（没有数据）即将超过4个的上限。父节点分裂（同样是经过排序的），左二右二，中间第三个再升一级变为父节点。
   
   
   

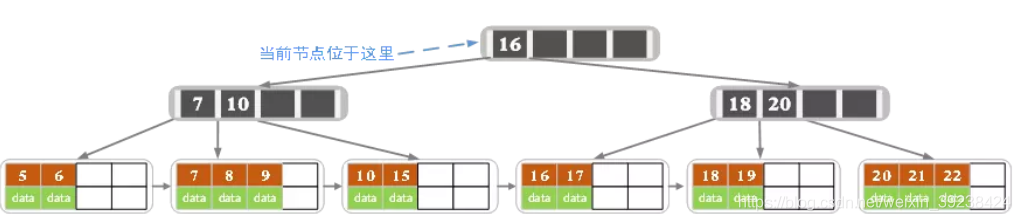
B+树的删除操作

1. 删除后无影响则直接删除并终止操作
   
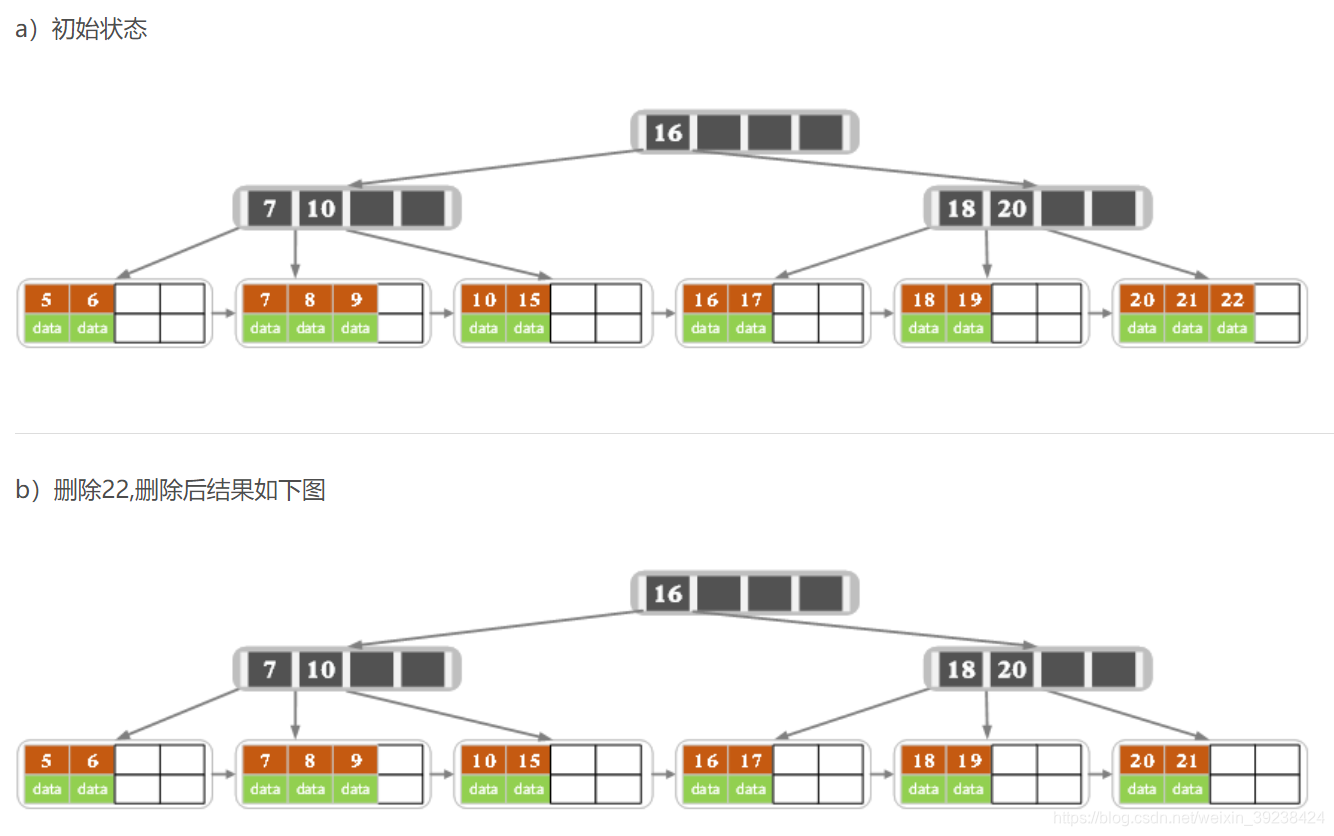
2. 删除时若子节点元素个数<2，相邻的子节点同时有多于2的元素，即可借位。同时更改父节点的关键字
   
   
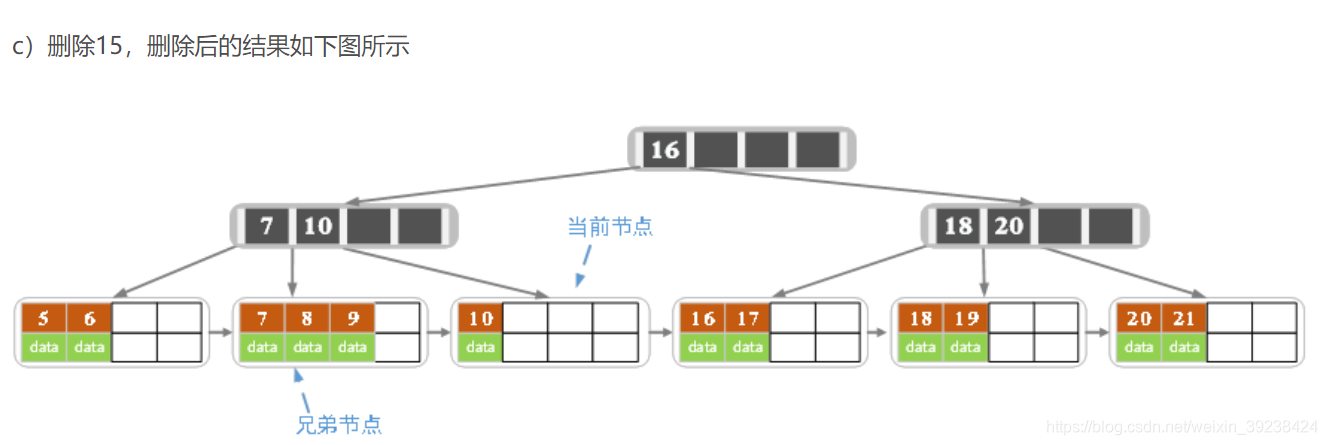
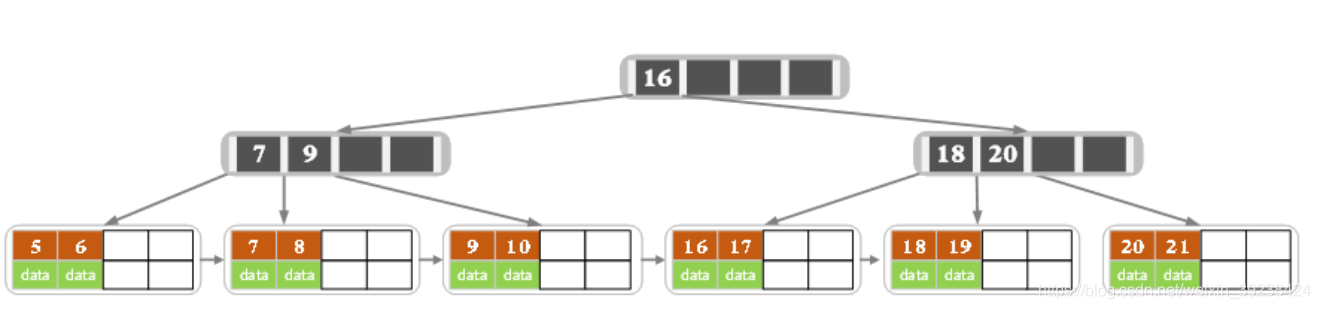
3. 如果领近的子节点没有多于的可以借，则进行合并（左右都可）。合并后，父节点元素<2了需要继续填充，父的兄弟也没有多余，就从父的父取值，造成元素的下沉。
   
   
   

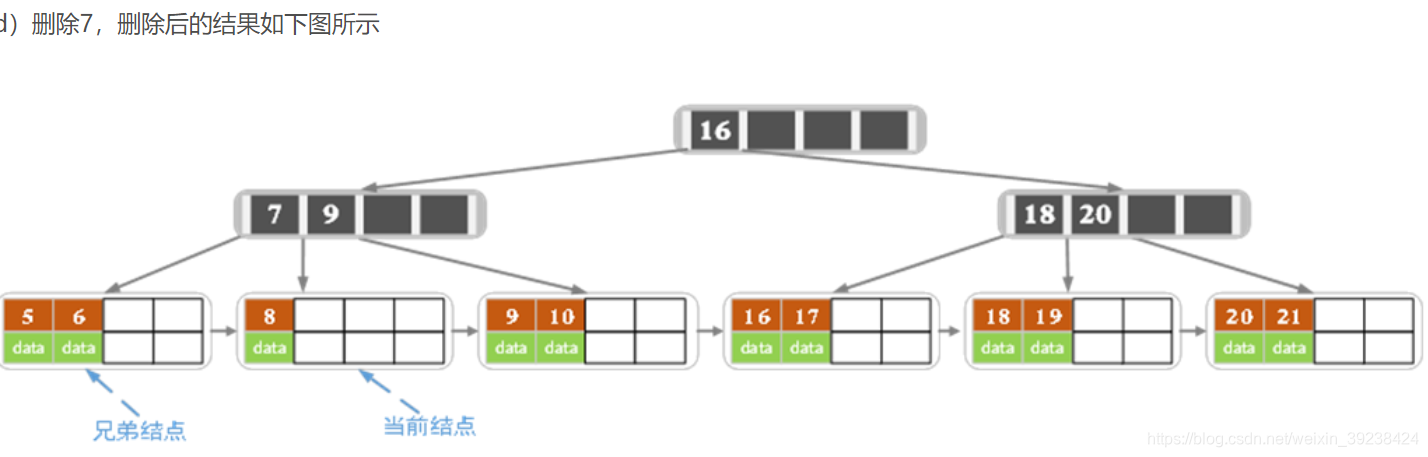
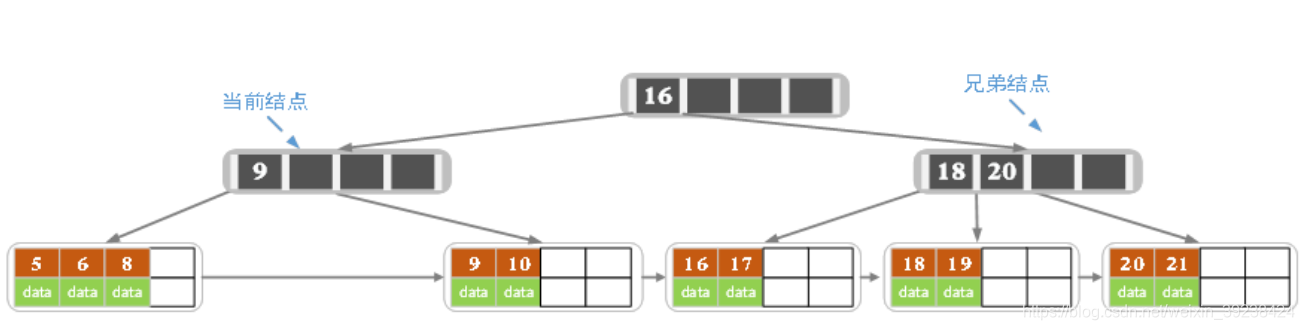
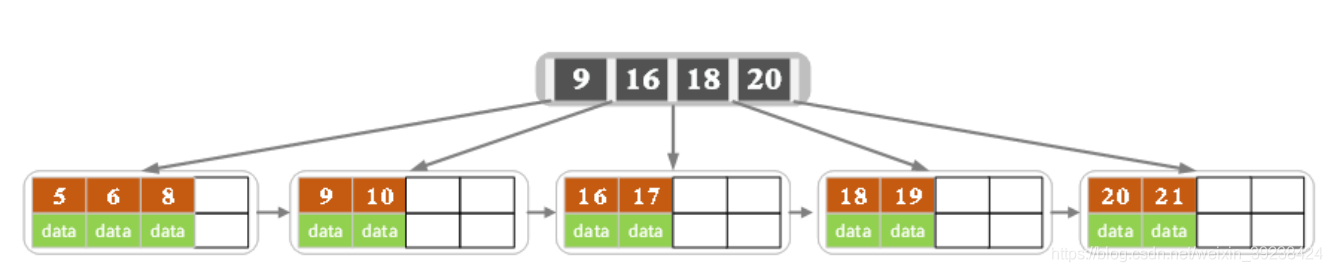
实际中的B+树：

8.4 代价模型
用B来表示当页中无浪费空间时数据页的数量，用R来表示每一页的记录数。读或写一个磁盘页的平均时间是D，处理一个记录的平均时间是C。将哈希函数应用于一个记录所需要的时间是H。对于树索引用F表示扇出。

I/O通常是数据库操作代价的主要部分。用读出或写入磁盘的页数来衡量I/O。

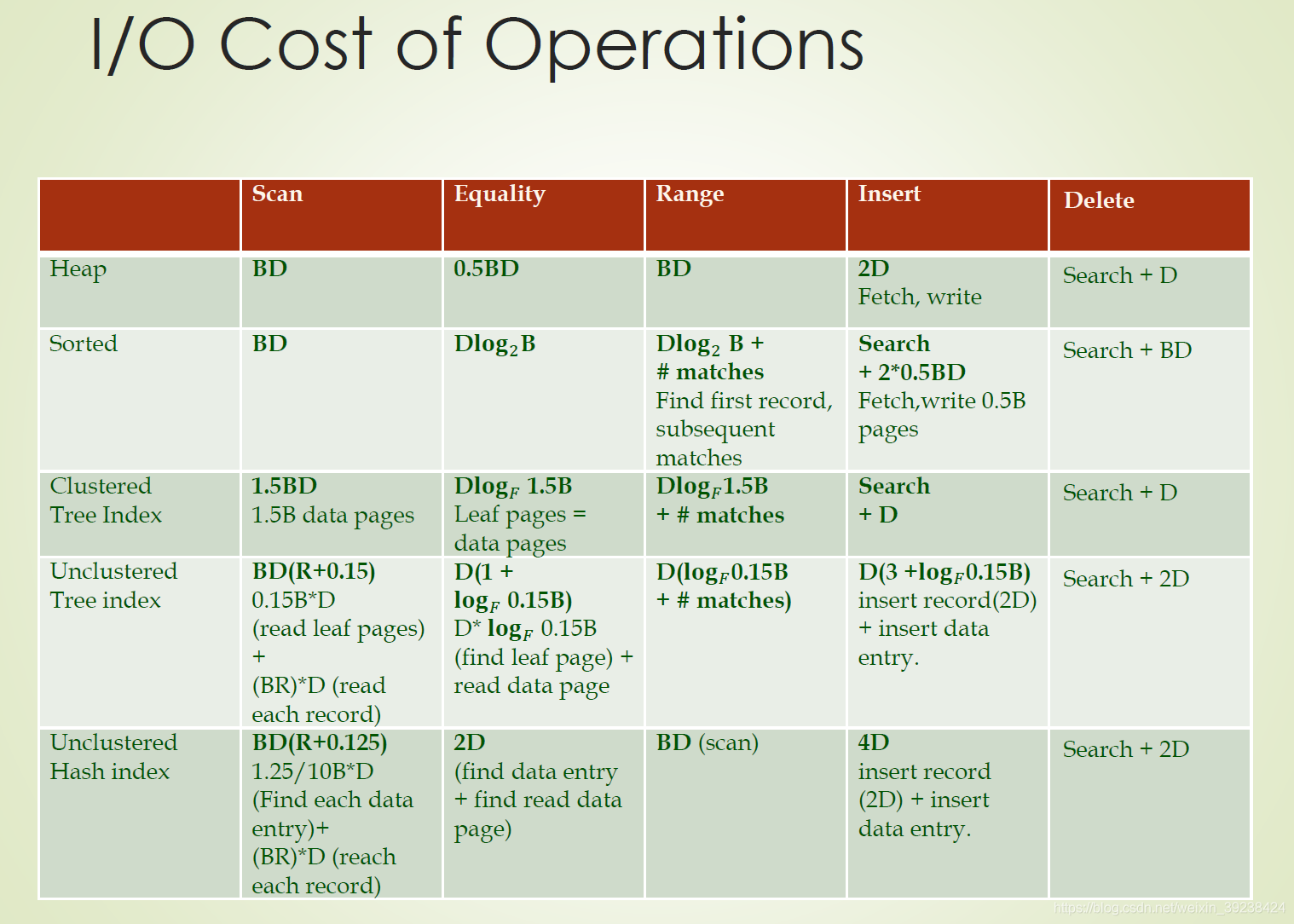
8.4.2堆文件
扫描：其代价为B（D+RC）。总共需要检索B页，每页需要花费D时间来读取，而且每页的R个记录需要花费C时间来处理。
等值选择型的搜索:
如果选择条件指定在候选码上。一般来说，如果该记录存在，并且搜索字段的值均匀分布，必须扫描文件的一半来找到这个记录。对于每一个检索的页，必须查看他的每一项，一查看他是否为需要的记录。因此代价为0.5B(D+RC)。但是如果不存在所搜索的记录，就必须扫描整个文件来证实其不存在。
如果选择条件不是指定在候选码上的，那么需要扫描整个文件，因为所要搜索的记录可能分布在文件中的任何位置。
范围选择型搜索：整个文件都需要扫描。因为是无序的，就不能确定他们在什么地方。所以其代价是B(D+RC)。
插入：假设记录总是插入在文件的末尾，必须取出文件的最后一页，加入记录，然后将该页写回。其代价为2D+C。
删除：首先必须找到这个记录，在从页中删除这个记录，然后再将页写回。

8.4.3排序文件
扫描：其代价为B(D+RC)。
等值选择型搜索：假定等值选择和排列顺序<age, sal>相匹配。或者说选择条件指定在至少是复合码的字段上。否则文件的排序对我们没有什么帮助，其访问代价和堆文件相同。

如果存在满足条件的记录 ，用二分法查找，可以在log2Blog2B步之内找出包含所要数据的第一页。每一步都需要一次磁盘I/O和两次比较。一旦找到所要的页， 第一个满足条件的记录也可以用二分法找到，代价为Clog2RClog2R,所以总代价为Dlog2B+Clog2RDlog2B+Clog2R.
范围选择型搜索:假定范围搜索和复合码相匹配，那么范围搜索就是多个等值搜索。第一步和等值搜索一样，定位所在的页，然后在页内找出所有满足范围选择条件的数据记录。其代价为搜索代价加上检索满足搜索条件的记录集的代价。

插入：如同数组的插入，在找到插入的槽，插入数据后，所有之后的数据都要向后移动一个槽的位置。Dlog2 B+Clog2 R+B(D+RC)Dlog2 B+Clog2 R+B(D+RC).
删除：首先必须找到这个记录，然后将将记录删除，并将修改后的页写回。和插入一样还需要修改被删除位置之后的页。所以其代价和插入相同。

8.4.4聚簇文件
大量文件显示，在聚簇文件中其页的占满率通常为67%，因此物理数据页大致为1.5B。

扫描：其代价为1.5B(D+RC)。
等值选择型搜索：假设等值选择与搜索码<age, sal>相匹配。如果存在满足条件的记录的话可以在logF1.5RlogF1.5R步内找到包含所要记录的页，即从根节点到恰到的叶节点的检索。一旦找到了那一页就可以用二分法查找满足条件的记录。所以其代价为DlogF1.5B+Clong2RDlogF1.5B+Clog2R,这与排序文件相比，在性能上有所提高。
范围选择型搜索：这类似于很多条件的等值选择。
插入:要插入一个数据记录，首先找到叶子页，然后在页内找到插入位置，直接插入。然后将型的页面写回。所以总代价为DlogF1.5B+Clog2R+DDlogF1.5B+Clog2R+D。
删除：与插入的代价相同。

8.4.5具有非聚簇树索引的堆文件
索引中叶子页的个数依赖于数据项的大小。假设索引中的每一个项的大小是一个雇员数据记录大小的1/10。叶子页的空间占用率为67%。那么索引中叶子页的个数为0.1（1.5B）。也就是0.15B。
同理一页中数据项的数量为10（0.67R）。

• 扫描：取出所有数据项的代价是0.15B(D+6.7RC)。根据数据项取出所有数据记录的代价是BR(D+C)。
• 等值选择型搜索：假设等值选择与排列序列相匹配，如果存在满足条件的项，就可以在logF0.15BlogF0.15B步之内定位到所要数据项的页，即取出所有从根到叶子的页。一旦找到这个页，那么在页内就可以用二分法的方式找到满足条件的数据项，其代价为Clog26.7RClog26.7R，第一个满足条件的数据记录就可以用一次I/O从雇员文件中取出。其代价为DlogF0.15B+Clog26.7R+DDlogF0.15B+Clog26.7R+D。
• 范围选择型搜索：类似于多个条件的等值选择型搜索。
• 插入：首先要以2D+C的代价，将记录插入到堆文件中，然后将相应的数据项插入到索引中。找到正确的叶子页，DlogF0.15B+Clog26.7RDlogF0.15B+Clog26.7R，添加新的数据项后写回到叶子页加上代价D.
• 删除：找到家写回，总共DlogF0.15B+Clog26.7R+D+2DDlogF0.15B+Clog26.7R+D+2D。

8.4.6具有非聚簇哈希索引的堆文件
页面占有率为80%, 所以总页数为1.25（0.1B） = 0.125B。每页中的数据项数目为10*0.8R = 8R。

• 扫描：数据项检索代价：0.125B(D+RC)。然而对于每一项都要花费一次I/O来取出数据记录。所以，其代价为BR(D+C)。
• 等值选择型搜索：找到数据项所在页的代价为H。假设这个桶只包含一页那么检索它的代价为D.扫描这个页的代价为0.5（8R）C = 4RC。从雇员文件中取出记录需要花费代价D。所以总的代价为H+2D+4RC。
• 范围选择型搜索：哈希对此没有什么优势，需要进行全文件扫描。
• 插入：首先将数据写到文件中，代价为2D+C。然后将索引加上去，代价为H+2D+C。
• 删除：搜索代价H+2D+4RC，更新数据单元代价2D。

索引
B+树索引：按照B+树的规则进行索引
hash索引：Hash索引结构的特殊性，其检索效率非常高，索引的检索可以一次定位，不像B-Tree索引需要从根节点到枝节点，最后才能访问到页节点这样多次的IO访问，所以Hash 索引的查询效率要远高于 B-Tree索引。（仅限于查询=或者！=，in）