METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS 翻译（一）

METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS（一）

分章节更新，剩下两部分一周内上传

1. 介绍和定义

在本手册中，我们考虑了以下问题

定义1.1. 最小二乘问题

寻找 $x^{\ast }$，即以下式子的局部最小值
$$F(x\text{x}x)=\frac{1}{2}\sum _{i=1}^m(f_i(x\text{x}x){)}^2\text{\hspace{1em}(1.1)}$$
其中，$f_i:{\mathbb{R}}^n\to \mathbb{R},i=1,...$,$m$ 由函数给定，并且 $m\ge n$。

$F(x)$ 的定义中的因子 $\frac{1}{2}$ 对 $x^{\ast }$ 没有影响。它是为了方便而引入的。

例子1.1.

最小二乘问题的一个重要来源是数据拟合。例如，考虑如下图所示的数据点 $(t_1,y_1),...,(t_m,y_m)$:

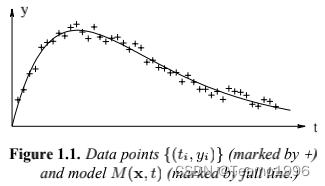
此外，我们还得到了一个拟合模型
$$M(x\text{x}x,t)=x_3{e}^{x_{1}t}+x_4{e}^{x_{2}t}$$

该模型取决于参数$x=[x_1,x_2,x_3,x_4{]}^T$。我们假设存在一个${x\text{x}x}^{\ast }$满足
$$y_i=M({x\text{x}x}^{\ast },t_i)+{ϵ}_i$$
其中{ϵi}\{\epsilon_i\}{ϵi​}是数据序列的（测量）误差，我们假定其行为类似于 “白噪声”。

对于任何给定的$x\text{x}x$,我们可以计算残差
$$\begin{array}{cc}& f_i(x)=y_i-M(x\text{x}x,t_i)\\ & =y_i-x_3{e}^{x_1{t}_i}-x_4{e}^{x_2{t}_i},i=1,...,m.\end{array}$$

对于最小二乘法的拟合，参数 ${x\text{x}x}^{\ast }$ 由最小化残差的平方之和来确定。这可以看作是一个当 $n=4$ 时定义1.1中的问题。$M({x\text{x}x}^{\ast },t)$ 的图形在图1.1中以实线显示。

最小二乘问题是更一般的问题的一个特殊变体：给定一个函数 $F:{\mathbb{R}}^n\to \mathbb{R}$，找到 $F$ 的一个参数，使这个所谓的目标函数或成本函数的值最小。

定义1.2. 全局最小值

给定 $F:{\mathbb{R}}^n\to \mathbb{R}$。寻找
x∗=argminx{F(x)}(1.2) \pmb{x}^*=argmin_{\pmb{x}}\{F(\pmb{x})\} \tag{1.2} xxx∗=argminxxx​{F(xxx)}(1.2)

这个问题在一般情况下很难解决，我们只介绍解决更简单的问题的方法，即寻找 $F$ 的局部最小化值，一个在一定区域内给出 $F$ 的最小值的参数向量。区域的大小由 $\delta$ 给出，其中 $\delta$ 是一个小的正数。

定义1.3. 局部最小值

给定 $F:{\mathbb{R}}^n\to \mathbb{R}$，寻找 ${x\text{x}x}^{\ast }$ 使得
$$F({x\text{x}x}^{\ast })\le F(x\text{x}x)for||x\text{x}x-{x\text{x}x}^{\ast }||<\delta \text{\hspace{1em}(1.3)}$$

在本介绍的其余部分，我们将讨论优化的一些基本概念。第2章简要回顾了对于通用的代价函数寻找局部最小值的方法。关于更多细节，可以参考 Frandsen et al (2004)。在第三章中，我们给出了专门针对最小二乘问题的方法。

我们假设代价函数 $F$ 是可微并且平滑的，这使得下面的泰勒展开是有效的，
$$F(x\text{x}x+h\text{h}h)=F(x\text{x}x)+{h\text{h}h}^{T}g\text{g}g+\frac{1}{2}{h\text{h}h}^{T}H\text{H}Hh\text{h}h+O(||h\text{h}h|{|}^3)\text{\hspace{1em}(1.4a)}$$

除非另有说明，$||\cdot ||$表示2-范数，$||h\text{h}h||=\sqrt{h_1^2+...+h_n^2}$。

其中 $g\text{g}g$ 是梯度,
$$g\text{g}g=\dot{F}(x\text{x}x)=\left[\begin{array}{c}\frac{\partial F}{\partial x_1}(x\text{x}x)\\ ⋮\\ \frac{\partial F}{\partial x_n}(x\text{x}x)\end{array}\right]\text{\hspace{1em}(1.4 b)}$$

$H\text{H}H$ 是海塞矩阵
$$H\text{H}H=\ddot{F}(x)=\left[\begin{array}{c}\frac{{\partial }^{2}F}{\partial x_i\partial x_j}(x\text{x}x)\end{array}\right]\text{\hspace{1em}(1.4 c)}$$

如果 ${x\text{x}x}^{\ast }$ 是一个局部最小值，并且 $||h\text{h}h||$ 足够小，那么我们就无法找到一个使得 $F$ 值更小的点${x\text{x}x}^{\ast }+h\text{h}h$。将这一观察与式（1.4a）结合起来我们可以得到

理论1.5. 局部最小值的必要条件

如果 ${x\text{x}x}^{\ast }$ 是局部最小值，则
$$g\text{g}g\ast =\dot{F}({x\text{x}x}^{\ast })=0$$

我们对满足必要条件的参数使用一个特殊的名称:

定义1.6. 驻点

如果
$${g\text{g}g}_s=\dot{F}({x\text{x}x}_s)=0$$
则 ${x\text{x}x}_s$ 被称为 $F$ 的一个驻点。

因此，局部最小值也是一个驻点，而局部最大值也是如此。一个既不是局部最大值也不是局部最小值的静止点被称为鞍点。为了确定一个给定的驻点是否是局部最小值，我们需要在泰勒级数（1.4a）中包含二阶项。代入 ${x\text{x}x}_s$ ，我们看到
$$F({x\text{x}x}_s+h\text{h}h)=F({x\text{x}x}_s)+\frac{1}{2}{h\text{h}h}^T{H\text{H}H}_{s}h\text{h}h+O(||h\text{h}h|{|}^3)\text{\hspace{1em}(1.7)}$$
其中 ${H\text{H}H}_s=\ddot{F}({x\text{x}x}_s)$

从海塞矩阵的定义（1.4c）可以看出，任何 $H\text{H}H$ 都是一个对称矩阵。如果我们要求 ${H\text{H}H}_s$ 是正定的，那么它的特征值需要大于某个数字 $\delta >0$（见附录A），并且
$${h\text{h}h}^T{H\text{H}H}_{s}h\text{h}h\ge \delta ||h\text{h}h|{|}^2$$

这表明，对于足够小的 $||h\text{h}h||$，（1.7）式右边的第三项将被第二项所支配。这个项是正的，所以我们得到

理论1.8. 局部最小值的充分条件

假设 ${x\text{x}x}_s$ 是一个驻点，并且 $\ddot{F}({x\text{x}x}_s)$ 是正定的。 那么 ${x\text{x}x}_s$ 是一个局部最小值。

如果 ${H\text{H}H}_s$ 是负定的，那么 ${x\text{x}x}_s$ 就是一个局部最大值。如果 ${H\text{H}H}_s$ 是不定的（即它的特征值有正有负），那么 ${x\text{x}x}_s$ 是一个鞍点。