0 摘要
调参千万回,看书第一回;
学习不总结,亲人两行泪。
1 PCA算法推导
1.1 PCA介绍
主成分分析(Principal components analysis),是一种降维方法,在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。简而言之就是,将高维数据通过线性变换投影到低维空间上。其关键是计算协方差矩阵。
1.2 PCA推导过程

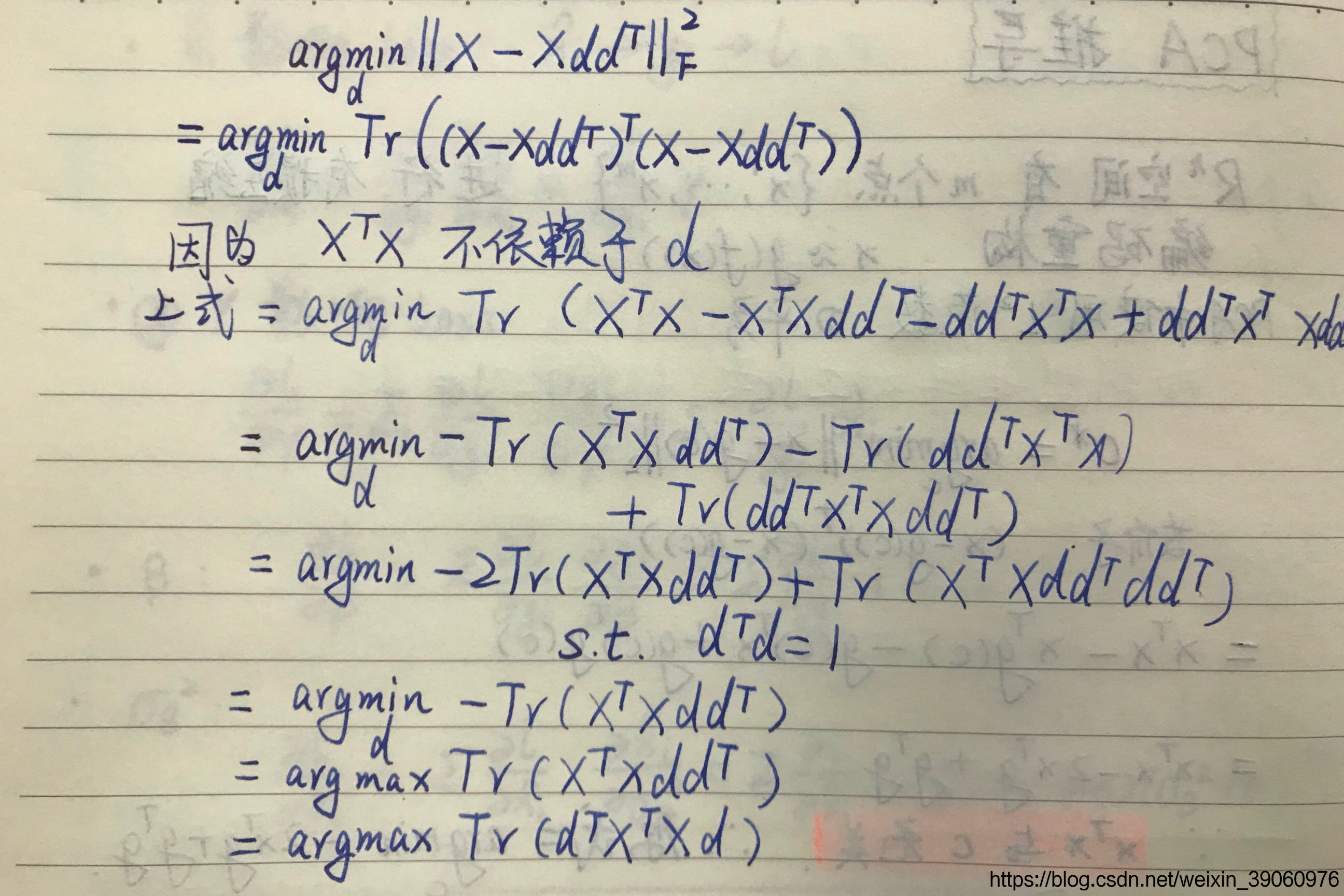
1.3 PCA与LDA异同
同:两者都是假设符合高斯分布的降维算法。
异:
(1)LDA是有监督的降维方法,PCA是无监督的。
(2)LDA降维最多降到类别数K-1的维数,PCA没有这个限制。
(3)LDA更依赖均值,如果样本信息更依赖方差的话,效果将没有PCA好。
(4)LDA可能会过拟合数据。


2 最小二乘解
2.1 线性方程组






 本文深入探讨了PCA(主成分分析)与LDA(线性判别分析)两种降维算法的原理与应用。PCA作为无监督学习方法,适用于数据压缩和噪音消除,而LDA作为有监督学习方法,特别适合于分类任务。文章详细讲解了两种算法的推导过程,对比了它们之间的异同,并讨论了各自的适用场景。
本文深入探讨了PCA(主成分分析)与LDA(线性判别分析)两种降维算法的原理与应用。PCA作为无监督学习方法,适用于数据压缩和噪音消除,而LDA作为有监督学习方法,特别适合于分类任务。文章详细讲解了两种算法的推导过程,对比了它们之间的异同,并讨论了各自的适用场景。
















 4085
4085

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








