课程前言:
arg max的参数是函数最大化的某个函数的域的点,与全局最大值相比参数函数的最大输出,arg max指的是函数输出尽可能大的输入或参数
闭式解:
给出任意自变量,就可以求出因变量
最小二乘法:
通过最小化误差的平方和寻找数据的最佳函数匹配
对微分得,
,
如果非奇异,则
有唯一解。
式(3.7)
分别对w,b求偏导,得:
,
令偏导数为0,得:
,(1)
,(2)
把(2)带入(1)得:
故
式(3.12)
由最小二乘法易得,若非奇异,w有唯一解。
然而现实任务中,往往不是满秩矩阵
式(3.27)
合并可得式(3.26)
当时,
当时,
合并得:
式(3.32)
将数据投影到直线上,则两类样本的中心在直线上的投影分别为,其中
为样本1的均值,
为样本2的均值。
其中为
投影前的协方差矩阵,故样本协方差为
式(3.35)
式(3.37)
,由拉格朗日公式易得,
,
,
为常数,若w为一个解,则aw 也为一个常数,忽略常数项,得,
,由于
为标量,故,
,带入(3.37)得,
式(3.48)
由于决策是基于,由于存在类别不平衡问题,故我们只要分类器的预测几率高于观测几率就判定为正例,即
,于是可得,
,因此
公式太多,码字太麻烦了→ →,直接上图吧。
字很丑,,,勉强看吧。
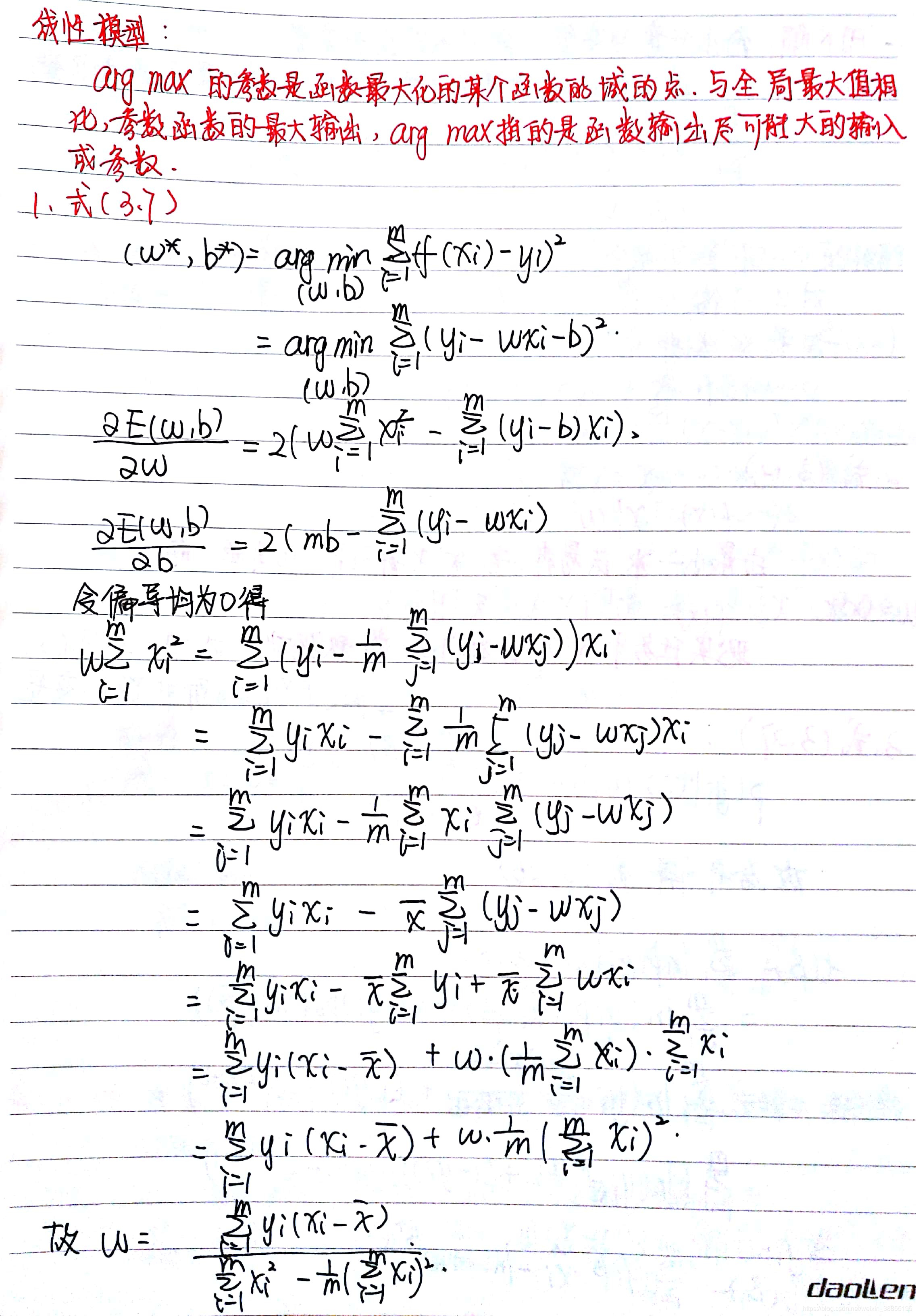















 本文深入探讨了机器学习中的关键优化算法,包括argmax的概念、闭式解的应用、最小二乘法原理及其在非满秩矩阵情况下的挑战。通过详细的数学推导,解释了如何求解参数w和b,以及在类别不平衡问题下的决策调整策略。
本文深入探讨了机器学习中的关键优化算法,包括argmax的概念、闭式解的应用、最小二乘法原理及其在非满秩矩阵情况下的挑战。通过详细的数学推导,解释了如何求解参数w和b,以及在类别不平衡问题下的决策调整策略。
















 1668
1668

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








