64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

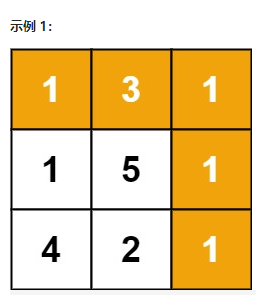
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思想：
// 整个问题的数字和最小是由 这问题的子问题的数字最小组成的 按照这个特性，所以使用动态规划
// 行走路线递推公式 f(m , n) = f(m - 1, n) + f(m, n - 1)
// 没走一步，判断当前走的这一步，是否使得当前的节点到起点位置的数字总和为最小
// 判断数据最小是在执行当前一步的时候，计算出向右的路径值和向下的路径值，然后取小的那个值作为当前路径的最小值

// 自底向上
int sum(int **grid, int m, int n)
{
    int total = 0;
    int i, j;
    for (i = 0; i < m + 1; i++) {
        for (j = 0; j < n + 1; j++) {
            total += grid[i][j];
        }
    }

    return total;
}


// 自底向上
int minPathSum(int** grid, int gridSize, int* gridColSize){

    int m = gridSize;
    int n = *gridColSize;    
    int **arr = (int **)malloc(sizeof(int *) * m * n);
    int i, j;
    int min_sum = 0;

    for (i = 0; i < m; i++) {
        arr[i] = (int *)malloc(sizeof(int) * n);
        memset(arr[i], 0, n);
    }

    for (i = 0; i < m; i++) {
        arr[i][0] = sum(grid, i, 0);
    }

    for (j = 0; j < n; j++) {
        arr[0][j] = sum(grid, 0, j);
    }

    for (i = 1; i < m; i++) {
        for (j = 1; j < n; j++) {
            int tmp_min = 0;
            if (arr[i - 1][j] < arr[i][j - 1]) {
                tmp_min = arr[i - 1][j];
            } else {
                tmp_min = arr[i][j - 1];
            }

            arr[i][j] = tmp_min + grid[i][j];
        }
    }
    min_sum = arr[m - 1][n - 1];

    for (i = 0; i < m; i++) {
        free(arr[i]);
        arr[i] = NULL;
    }
    free(arr);
    arr = NULL;

    return min_sum;
} 


// 自顶向下
// 思路一：搜索出来所有路径和，然后找最小的值---有点麻烦，不想实现，没啥价值
// 思路二：和自底向上一样，在寻找的中间就进行判断，然后找出最小值 --- 但是无法确定当前搜索的路径是最小值，比如我下面这个算法
int get_min_path(int **grid, int m, int n) 
{
    int path = 0;
    if ((m == 0) && (n != 0))  {
        int i;
        for (i = 0; i < n + 1; i++) {
            path += grid[0][i];
        }
        return path;
    }

    if ((m != 0) && (n == 0))  {
        int i;
        for (i = 0; i < m + 1; i++) {
            path += grid[i][0];
        }
        return path;
    }

    path = path + grid[m][n];
    if (grid[m - 1][n] < grid[m][n - 1]) {
        path += get_min_path(grid, m - 1, n);
    } else {
        path += get_min_path(grid, m, n - 1);
    }

    return path;

}


// 自顶向下
int minPathSum(int** grid, int gridSize, int* gridColSize){
    int m = gridSize;
    int n = *gridColSize;

    if ((m == 1) && (n == 1)) {
        return grid[m - 1][n - 1];
    }

    return get_min_path(grid, m - 1, n - 1);

}

复杂度：
自底向上：时间复杂度 O(mn)，空间复杂度 O(mn)
自顶向下：时间复杂度O(mn)，空间复杂度O(mn)