loss函数总结

损失函数：损失项(loss term)和正则项(regularization term)组成

回归问题中:

1)MSE（L2损失）  :

2)绝对值(L1 损失)：

3）Huber损失（平滑平均绝对误差）：，当  小于一个事先指定的值  时，变为平方损失，大于  时，则变成类似于绝对值损失

 

 

总结：

1）使用绝对误差（MAE）对于异常值更鲁棒，MSE对于异常值更敏感

     如果异常值表示的反常现象对于业务非常重要，我们就应当使用MSE。另一方面，如果我们认为异常值仅表示损坏数据而已，那么我们应当选择MAE作为损失函数。

2）MAE用于训练神经网络的一个大问题就是，它的梯度始终很大，这会导致使用梯度下降训练模型时，在结束时遗漏最小值。对于MSE，梯度会随着损失值接近其最小值逐渐减少，从而使其更准确。

3）Huber损失同时具备MSE和MAE这两种损失函数的优点。不过，Huber损失函数也存在一个问题，我们可能需要训练超参数δ，而且这个过程需要不断迭代

 

MSE均方误差（L2 loss）
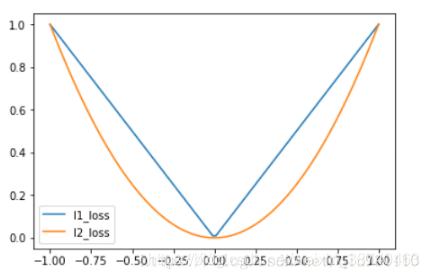
1.代码展示MAE和MSE图片特性

import tensorflow as tf
import matplotlib.pyplot as plt
sess = tf.Session()
x_val = tf.linspace(-1.,-1.,500)
target = tf.constant(0.)

#计算L2_loss
l2_y_val = tf.square(target - x_val)
l2_y_out = sess.run(l2_y_val)#用这个函数打开计算图

#计算L1_loss
l1_y_val = tf.abs(target - x_val)
l1_y_out = sess.run(l1_y_val)#用这个函数打开计算图

#打开计算图输出x_val，用来画图
#用画图来体现损失函数的特点
x_array = sess.run(x_val)
plt.plot(x_array, l1_y_out, 'b--', lable = 'L1_loss')
plt.plot(x_array, l2_y_out, 'r--', lable = 'L2_loss')

 

 

分类问题中：

1）0-1损失：

2）log损失：

3）Hinge(合页) 损失 :

4）指数损失：

 

5）Triplet Loss： 

常用在人脸识别中，优点：细节区分 （其中加入了对差异性的度量）

                               缺点：1)收敛慢，难训练       2）容易过拟合