1143. 最长公共子序列

晴天M雨天

于 2022-07-18 19:34:24 发布

阅读量68

点赞数

CC 4.0 BY-SA版权

文章标签：算法 leetcode 动态规划

本文链接：https://blog.youkuaiyun.com/weixin_38738049/article/details/125858611

这篇博客探讨了如何使用动态规划来解决字符串的最长公共子序列问题。作者介绍了核心思路，即通过二维数组记录每个子串的最大公共长度，并给出了关键的转移规则。当字符相等时，公共子串长度加一；不等时，取前一状态的最大值。最后，博主强调了转换人类思维为机器思维以及理解计算机执行逻辑的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这里有一个思维方式的改变，这里需要一定的经验
此题可以看做是 s1=”****a”
S2=”****a”
如果最后一个字母相同就比较n-1 这样子问题就出来了
字符串的变化问题就需要变成一个二维数组
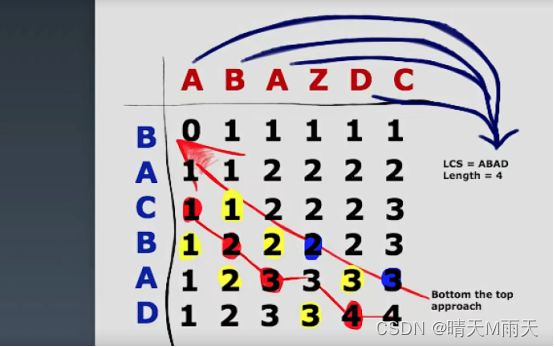
在这里插入图片描述

这个表的坐标中的数字含义是当前行的字串在当前列字串中的最大公共字串

B A 没有是0
B AB 有一个是1
B ABA 有一个是1
B ABAZ 有一个是1
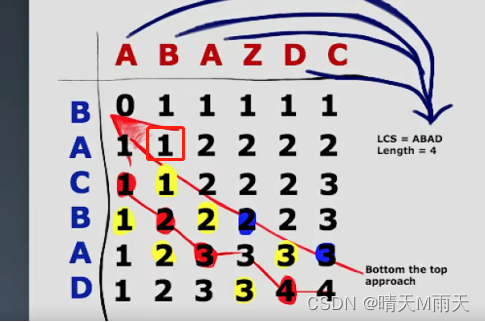
在这里插入图片描述

如果最后两个字符不相等 ，如图所示 就需要考虑 BA  A ，B  AB 两种情况的最大值，
如果 字符相等    则等于 dp[i−1][j−1]+1
动态规则小结 
 1打破自己的思维，形成机器思维

2 计算机只会 if else loop
3找重复性

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            char c1 = text1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.charAt(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}