傅里叶变换后面的到底有什么小秘密

从简单分解到傅里叶分析的正交分解

最新推荐文章于 2022-09-20 17:14:27 发布

修行进行时

最新推荐文章于 2022-09-20 17:14:27 发布

阅读量565

点赞数

分类专栏：数学知识

数学知识专栏收录该内容

10 篇文章

订阅专栏

博客从纸币面额设为1、2、5的原因引出为求简便进行分解、正交化及内积的概念。指出傅里叶分析就是进行“正交分解”，先介绍三维直角坐标系中基和内积，再扩展到基为函数的情况，说明傅里叶变换本质是正交分解，还给出变换和逆变换公式。

转自大神：https://zhuanlan.zhihu.com/p/40396861

大家有没有想过一个问题，为什么全世界都把自己的纸币面额设成1、2和5这三个数字？

这么选择是一种偶然还是必然？背后有什么秘密吗？其实答案没有什么太高深的，就是“简便”而已。因为人类经过多年的进化，形成了一种不可或缺的生存能力，那就是尽量将复杂的分解为简单的问题，比如：人们就发现虽然事物的价格千千万，我们总是可以用几种简单的数字叠加起来。而1、2和5这三个数字恰恰是10进位制里面最简便的组合。

为了“简单”而进行“分解”，为了更好的“分解”，人类又发明了“正交”的概念。何谓正交呢，它其实脱胎于“垂直”而又有更丰富的内涵。我们知道在垂直坐标系中，三个坐标轴的相互垂直的，这样的好处是各个轴向之间是独立的，互不干扰的。当然，这些描述都是定性的，对于严谨的数学家和工程师而言，这是不可接受的。于是，又有一个新的概念引入了:“内积”，当内积为零的时候，两个量就是正交的。

整理一下我们的思路：我们想要“简单”，要进行“分解”，想要更好的“分解”，要进行“正交化”，想要定量描述“正交化”，规定“内积”为零为“正交”。总的逻辑是这样的：简单→分解→正交→内积。

说了这么多，这和傅里叶分析有什么关系？现在我要告诉大家：傅里叶分析就是进行“正交分解”，不理解细节没关系，领会到了这个概念，就理解一半了。为了严谨（实际上很不严谨^_^），我们需要将逻辑关系反过来，先从内积说起。

在三维直角坐标系里面，任何一个坐标轴的方向上长度为的向量称之为一个基，相互垂直的基称之为正交基：（1,0,0）代表轴的基，（0,1,0）代表轴的基，（0,0,1）代表轴的基。假设 $\bar{x}=（a_1,b_1,c_1）$ , $\bar{y}=(a_2,b_2,c_2)$ ，

规定内积为： $< \bar{x},\bar{y}>=<(a_1,b_1,c_1),(a_2,b_2,c_2)>=a_1a_2+b_1b_2+c_1c_2$

一个很简单的结论： $<(1,0,0),(0,1,0)>=1\times0+0\times1+0\times0=0$ ,说明任意两个基确实是正交的。 $<(1,0,0),(1,0,0)>=1\times1+0\times0+0\times0=1$ ，说明向量与自己的内积是一个常数。那如何表示任意一个向量呢？比如 v=（5,2,7）在线性代数里面，我们是这么做的：

A=< v,x>=<(5,2,7),(1,0,0)>=5 （1）

B=< v,y>=<(5,2,7),(0,1,0)>=2 （2）

C=< v,z>=<(5,2,7),(0,0,1>=7 （3）

于是， v=Ax+By+Cz ，相信得出以下结论是很容易的：内积相当于一种“投影”操作，任意向量与基之间的内积就是该向量在基所在方向的投影，内积的结果就是系数。

前面我们说的“基”都是常数，这是很容易理解的，我们生活在三维的世界里，我们教材里面从初中就开始介绍这些东西，再熟悉不过了。下面我们要对上面的讨论稍微进行扩展，大家会看到将会有哪些有意思的事情发生。

假如基不再是一个向量，而是一个函数，会有什么结果？比如我们如果假设 f,g 是两个函数，并且规定内积定义为： $< f,g>=\int_{-\infty}^{+\infty} f\times \bar{g}$ ，（其中 $\bar{g}$ 表示共轭的意思，是为了在复数域中计算方便而引入的）。我之前写的帖子：
https://zhuanlan.zhihu.com/p/40317763

以及：https://zhuanlan.zhihu.com/p/40302967

介绍了自然常数以及复指数 $e^{ix}$ 神奇特性。我们不妨将 $e^{ix}$ 代入 f,g ,看看会出现什么。假设 $f=e^{i\omega_1t}$ ， $g=e^{i\omega_2t}$ ，则 f,g 的内积为：

$< f,g>=\int_{-\infty}^{+\infty}e^{i\omega_1t}e^{-i\omega_2t}dt=\int_{-\infty}^{+\infty}e^{i(\omega_1-\omega_2)t}dt$

当 $\omega_1=\omega_2$ 时，细心的同学可能注意到，这个积分是无穷大，这个没关系，在广义函数里面这是允许的，为了不影响我们的阅读体验，暂不细说，我们用一个符合来表示这个积分的结果： $2\pi\cdot\delta(\omega_1-\omega_2)$ 。

当 $\omega_1\ne\omega_2$ 时，上面的积分等于多少呢？在https://zhuanlan.zhihu.com/p/40302967

里面，我们介绍了 $e^{ix}$ 本质上是一个运动的单位圆。

x=linspace(0,2*pi,50);%0到2pi之间均匀布置50个点；
n=5000;%此处可将n设成20,50，500或其他
e_ix=(1+x*1i./n).^n;
compass(e_ix);
figure;
polarplot(e_ix);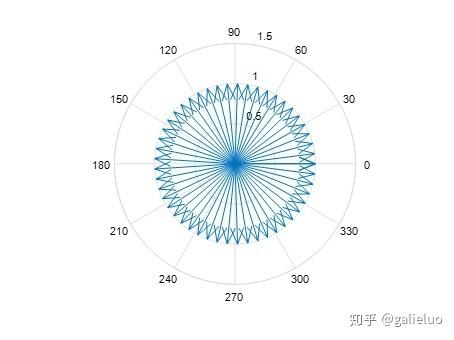

若 $\omega_1\ne\omega_2$ ， $e^{i(\omega_1-\omega_2)t}$ 就是一个绕原点旋转的单位圆啊，由于对称性，我们可以很容易得到： $< f,g>=< e^{i\omega_1t}, e^{i\omega_2t}>=\int_{-\infty}^{+\infty}e^{i(\omega_1-\omega_2)t}dt=0$ ，等等，内积等于零？这说明什么？这说明正交啊，这说明 $e^{i\omega t}$ 在这种内积的定义下是一族正交基啊，更深刻的数学知识可以证明，在一定条件下，它不仅是正交的，还是完备的，也就是说，只要满足一定的条件，任何函数都可以用 $e^{i\omega t }$ 叠加出来。

$f(t)=\sum_{\omega=-\infty}^{+\infty}{A_\omega e^{i\omega t}}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t}d\omega$ （4）

这个式子的含义为：在一定条件下，任意函数（ f(t) ）都可以由完的正交基 $e^{i\omega t}$ 叠加而成，每个正交基对应的系数为 $F(\omega)$ 。（ $1/{2\pi}$ 的引入是为了计算方便，傅里叶变换有多种形式，也有不带 $1/{2\pi}$ ，这里采用了最通用的形式）。

根据公式（1、2、3），系数 $F(\omega)$ 可以由内积计算而来：

$F(\omega)=< f(t),e^{i\omega t}>=\int_{-\infty}^{+\infty}f(t)e^{-i\omega t}dt$ （5）

因此，傅里叶变换的本质可以看成是正交分解： f(t) 和 $e^{i\omega t}$ 求内积的时候， f(t) 中只有频率为 $\omega$ 的分量才会有内积的结果，其余分量的内积为0，积分值是时间从负无穷到正无穷，可以看成是 f(t) 整个信号在 $e^{i\omega t}$ 上的投影，只要给定一个频率 $\omega$ ，都会对应一个系数 $F(\omega)$ 来。