概述
- 逻辑斯蒂回归实质是对数几率回归(广义的线性回归),是用来解决分类问题的。
- 其中sigmoid用来解决二分类问题,softmax解决多分类问题,sigmoid是softmax的特殊情况。
- 数学建模直接针对分类可能性建模。
- 参数学习可用极大似然估计或贝叶斯估计,利用极大似然估计求得的目标函数与交叉熵损失一致。
- 梯度下降之sigmoid和softmax函数的求导。
一、基本的数学概念和推导
1. logistic函数(也叫logistic分布函数)
- logistic函数形如“S”,具体公式如下:
f(x)=L1+e−k(x−x0) f ( x ) = L 1 + e − k ( x − x 0 )
其中: x0 x 0 代表中点, L L 代表函数的最大值,代表曲线的陡度。 - 标准的logistic函数(即sigmoid函数),
x0=0,k=1,L=1
x
0
=
0
,
k
=
1
,
L
=
1
,即:
f(x)=11+e−x f ( x ) = 1 1 + e − x

2.sigmoid函数
概念
sigmoid是logistic函数的特例,如上所述, x0=0,k=1,L=1 x 0 = 0 , k = 1 , L = 1 时,logistic函数就退化为sigmoid函数。
f(x)=11+e−x f ( x ) = 1 1 + e − x考察sigmoid函数的性质
- 关于(0,0.5)中心对称
- 值域: f(x)∈ f ( x ) ∈ [0,1]
- 梯度饱和: x→∞,f(x)→0 x → ∞ , f ( x ) → 0
- 简单变形:
f(x)=11+e−x=ex1+exex1+ex=1−e−x1+e−x→f(x)=1−f(−x) f ( x ) = 1 1 + e − x = e x 1 + e x e x 1 + e x = 1 − e − x 1 + e − x → f ( x ) = 1 − f ( − x ) - 导数
f′(x)=f(x)×(1−f(x))∈[0,14] f ′ ( x ) = f ( x ) × ( 1 − f ( x ) ) ∈ [ 0 , 1 4 ] ,梯度饱和的原因。推导如下:
f′(x)=(11+e−x)′=e−x(1+e−x)2=e−x1+e−x×11+e−x=11+ex×ex1+ex(变形一)=f(x)×(1−f(x)) f ′ ( x ) = ( 1 1 + e − x ) ′ = e − x ( 1 + e − x ) 2 = e − x 1 + e − x × 1 1 + e − x = 1 1 + e x × e x 1 + e x ( 变 形 一 ) = f ( x ) × ( 1 − f ( x ) )
- 应用
- 神经网络中的激活函数
- 分类问题:二项逻辑回归(sigmoid回归)
3.softmax函数
- 基本概念
softmax也被称为指数规范函数,是logistic函数的泛化。通过把一个k维空间的向量 z z 的值(具有任意性)压缩到另一个k维空间的向量,它的每一个值都在(0,1)并且所有值的和为1(具有天然的概率分布的特性),数学表示如下:
σ:RK→{z∈RK|zi≥0,∑i=1Kzi=1}σ(zj)=ezj∑k=1Kezk,j=1,2,...,K σ : R K → { z ∈ R K | z i ≥ 0 , ∑ i = 1 K z i = 1 } σ ( z j ) = e z j ∑ k = 1 K e z k , j = 1 , 2 , . . . , K
矩阵形式:
σ(z)=⎡⎣⎢⎢⎢⎢σ(z1)σ(z2)...σ(zK)⎤⎦⎥⎥⎥⎥=1∑Kk=1ezk⎡⎣⎢⎢⎢⎢ez1ez2...ezK⎤⎦⎥⎥⎥⎥ σ ( z ) = [ σ ( z 1 ) σ ( z 2 ) . . . σ ( z K ) ] = 1 ∑ k = 1 K e z k [ e z 1 e z 2 . . . e z K ]
其中k=2即为sigmoid函数,具体推导见下文,主要利用了softmax函数的参数冗余的性质(令 z1=0 z 1 = 0 )。 - 导数
考察其中一维的输出 σ(zi) σ ( z i ) 对于任意的输入 zj z j 的情况,从而可以扩展到任意一维的导数。
case1:i∂σ(zi)∂zjcase2:i∂σ(zi)∂zjonecase:∂σ(zi)∂zj=j=ezi∑Kk=1ezk−(ezi)2(∑Kk=1ezk)2=ezi∑Kk=1ezk(∑Kk=1ezk)2−(ezi)2(∑Kk=1ezk)2=σ(zi)−σ(zi)2=σ(zi)(1−σ(zi))≠j=−eziezj(∑Kk=1ezk)2=−σ(zi)σ(zj)=σ(zi)(δi,j−σ(zj)),i=j→δi,j=1 else: δi,j=0 c a s e 1 : i = j ∂ σ ( z i ) ∂ z j = e z i ∑ k = 1 K e z k − ( e z i ) 2 ( ∑ k = 1 K e z k ) 2 = e z i ∑ k = 1 K e z k ( ∑ k = 1 K e z k ) 2 − ( e z i ) 2 ( ∑ k = 1 K e z k ) 2 = σ ( z i ) − σ ( z i ) 2 = σ ( z i ) ( 1 − σ ( z i ) ) c a s e 2 : i ≠ j ∂ σ ( z i ) ∂ z j = − e z i e z j ( ∑ k = 1 K e z k ) 2 = − σ ( z i ) σ ( z j ) o n e c a s e : ∂ σ ( z i ) ∂ z j = σ ( z i ) ( δ i , j − σ ( z j ) ) , i = j → δ i , j = 1 e l s e : δ i , j = 0
二、二项逻辑回归(sigmoid回归)
1.回归与分类
逻辑回归是用来解决分类问题的,名称中的回归实质是对数几率回归的含义。
- 几率与对数几率
几率(odds)即一件事发生的相对可能性。对于给定的x,分为正例的可能性为y则反例的可能性为1-y,有如下定义:
odds=y1−ylog odds=lny1−y o d d s = y 1 − y l o g o d d s = l n y 1 − y - 对数几率回归
对于逻辑回归的模型 y=11+e−wTx+b y = 1 1 + e − w T x + b ,代入对数几率,则有:
lny1−y=wTx+b l n y 1 − y = w T x + b
即实质上是用右边的线性回归模型去拟合对数几率,因此也被称为对数几率回归。
2.二项逻辑回归的数学建模
分类模型(记sigmoid函数为 θ θ )
p(Y=1|x)p(Y=0|x)f(x)=θ(wTx+b)=1−θ(wTx+b)=argmaxyip(yi|x),yi=0,1 p ( Y = 1 | x ) = θ ( w T x + b ) p ( Y = 0 | x ) = 1 − θ ( w T x + b ) f ( x ) = a r g max y i p ( y i | x ) , y i = 0 , 1
在给定的输入x下,上述两式分别求得Y=1和Y=0的概率,比较这两个概率值的大小,
将x分类到概率值大的那一类。参数学习
建模之后,要解决的问题就是确定模型中的参数。- MLE(极大似然估计)
假定随机变量不变,最大化似然函数对参数做出估计,简单介绍一下两种类型(连续和离散)的似然函数的求解方法。
离散型:
L(θ)=L(x1,x2,...,xn;θ)=∏ni=1p(xi;θ) L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = ∏ i = 1 n p ( x i ; θ )
连续性:
L(θ)=L(x1,x2,...,xn;θ)=∏ni=1f(xi;θ) L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = ∏ i = 1 n f ( x i ; θ )
形式看起来特别像,都是累乘的形式,只不过离散的是分布的累乘,而连续的是概率密度的累乘。实际应用中,一般用到的是对数似然函数 ,就是利用到log函数的性质(和的对数等于对数的积),方便运算。 - 二项逻辑回归的MLE
似然函数:l(w)对数似然函数:logl(w)对于二分类:p(yi|xi)推导:logl(w)=∏i=1np(yi|xi,w)=log∏i=1np(yi|xi)=∑i=1nlogp(yi|xi)=(p(yi=1|xi))yi×(p(yi=0|xi))1−yi=∑i=1nlog[(p(yi=1|xi))yi×(p(yi=0|xi))1−yi]=∑i=1nlog(p(yi=1|xi))yi+log(p(yi=0|xi))1−yi=∑i=1nyilogp(yi=1|xi)+(1−yi)logp(yi=0|xi)=∑i=1n∑k=01p(yi=k)logp(yi=k|xi)=∑i=1n∑k=01I(yi=k)logσ(yi;xi,w,b)(I为指示函数,yi取对应类别时为1) 似 然 函 数 : l ( w ) = ∏ i = 1 n p ( y i | x i , w ) 对 数 似 然 函 数 : l o g l ( w ) = l o g ∏ i = 1 n p ( y i | x i ) = ∑ i = 1 n l o g p ( y i | x i ) 对 于 二 分 类 : p ( y i | x i ) = ( p ( y i = 1 | x i ) ) y i × ( p ( y i = 0 | x i ) ) 1 − y i 推 导 : l o g l ( w ) = ∑ i = 1 n l o g [ ( p ( y i = 1 | x i ) ) y i × ( p ( y i = 0 | x i ) ) 1 − y i ] = ∑ i = 1 n l o g ( p ( y i = 1 | x i ) ) y i + l o g ( p ( y i = 0 | x i ) ) 1 − y i = ∑ i = 1 n y i l o g p ( y i = 1 | x i ) + ( 1 − y i ) l o g p ( y i = 0 | x i ) = ∑ i = 1 n ∑ k = 0 1 p ( y i = k ) l o g p ( y i = k | x i ) = ∑ i = 1 n ∑ k = 0 1 I ( y i = k ) l o g σ ( y i ; x i , w , b ) ( I 为 指 示 函 数 , y i 取 对 应 类 别 时 为 1 )
上述最后两步的推导需要注意,对于二分类问题, yi y i 取值为0或1,因此 p(yi=k) p ( y i = k ) 表示的是 yi y i 取到对应的类别时为1,对于一个样本 yi y i 只有一个取值,要不为0要不为1。上述的推导是成立的,为了统一表述的便利。
此时我们的参数学习问题转化为这样的问题:求极大似然函数时对应的 W,b W , b 。 - 损失函数与交叉熵
因为损失函数我们理解的是越小越好,因此这里这样定义成本函数:
损失函数:J(y,ŷ )=−1nlogl(w,b) 损 失 函 数 : J ( y , y ^ ) = − 1 n l o g l ( w , b )
此时我们的参数学习问题也即优化问题转化为最小化这样的损失函数: J(y,ŷ )=−1nlogl(w,b) J ( y , y ^ ) = − 1 n l o g l ( w , b ) 。
这里引入交叉熵的概念:
H(p,q)=−∑xp(x)logq(x) H ( p , q ) = − ∑ x p ( x ) l o g q ( x )
其中p表示的是真实分布,q表示的是拟合分布,所以交叉熵衡量的是两个分布的拟合情况。对应到我们根据MLE求得的损失函数,二者是一致的。因此这里有这样的结论,逻辑回归的MLE确定的损失函数即是交叉熵损失函数,更一般地,对于对数似然都有这样的结论。 - 梯度下降
这里简单给出推导,后续写一个逻辑回归的代码。
∂J(W,b)∂W∂J(W,b)∂bW−b−=−1n∑i1σ(yi;xi)σ(yk;xi)(δi,j−σ(yi;xi))xi(参考前面的softmax求导)=−1n∑i(δi,k−σ(yi;xi))xi=−1n∑iδi,k−σ(yi;xi)(这里的δi,k表示的是对于样本i是否被正确分类)=−∂J(W,b)∂W=−∂J(W,b)∂b(达到迭代伦次或者损失函数降到阈值以下停止) ∂ J ( W , b ) ∂ W = − 1 n ∑ i 1 σ ( y i ; x i ) σ ( y k ; x i ) ( δ i , j − σ ( y i ; x i ) ) x i ( 参 考 前 面 的 s o f t m a x 求 导 ) = − 1 n ∑ i ( δ i , k − σ ( y i ; x i ) ) x i ∂ J ( W , b ) ∂ b = − 1 n ∑ i δ i , k − σ ( y i ; x i ) ( 这 里 的 δ i , k 表 示 的 是 对 于 样 本 i 是 否 被 正 确 分 类 ) W − = − ∂ J ( W , b ) ∂ W b − = − ∂ J ( W , b ) ∂ b ( 达 到 迭 代 伦 次 或 者 损 失 函 数 降 到 阈 值 以 下 停 止 )
- MLE(极大似然估计)
三、多项逻辑回归(softmax回归)
1.基本概念
- softmax回归其实是逻辑回归的一般化形式,是二项逻辑回归的扩展和泛化。
- 所以多项逻辑回归即softmax回归,用来处理多分类问题。
2.数学建模
- 分类模型
p(y=j|X,W)=eXTwj∑Kk=1eXTwkp(y|x)=⎡⎣⎢⎢⎢⎢p(y=1|x)p(y=2|x)...p(y=K|x)⎤⎦⎥⎥⎥⎥=1∑kj=1exTwk⎡⎣⎢⎢⎢⎢exTw1exTw2...exTwK⎤⎦⎥⎥⎥⎥f(x)=argmaxyp(y=k|x) p ( y = j | X , W ) = e X T w j ∑ k = 1 K e X T w k p ( y | x ) = [ p ( y = 1 | x ) p ( y = 2 | x ) . . . p ( y = K | x ) ] = 1 ∑ j = 1 k e x T w k [ e x T w 1 e x T w 2 . . . e x T w K ] f ( x ) = a r g max y p ( y = k | x )
这样理解建模的过程,和二项逻辑回归类似,通过softmax求得实例属于每个类别的概率,最终选择概率最大的那一类作为输出。
换一种思路来理解,其实多项逻辑回归就是K个线性分类器再加上Softmax函数的非线性转换,最终映射到[0,1]区间的概率值,哪一个线性分类器对应的概率值大,输入就属于该分类! - 多分类与二分类的关系
下面通过对softmax推导,从数学的角度说明二分类与多分类的关系。
softmax函数具有冗余性质:
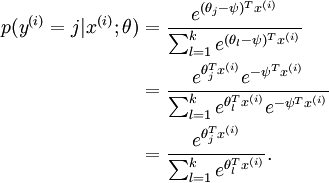
令 ψ=θk ψ = θ k ,则有:
p(yi=k|xi,W)=11+∑l=1k−1eWTxl+bp(yi=j|xi,W)=eWTxj+b1+∑l=1k−1eWTxl+b p ( y i = k | x i , W ) = 1 1 + ∑ l = 1 k − 1 e W T x l + b p ( y i = j | x i , W ) = e W T x j + b 1 + ∑ l = 1 k − 1 e W T x l + b
当k=2时,即为2分类问题,与二项逻辑回归的模型是一致的。 - 参数学习
与二项逻辑回归类似,也可从MLE推导得到和交叉熵一致的损失函数。
J(W,b)=−1n∑i=1n∑k=1KI(yi=k)logp(yi|xi,w,b)(I为指示函数,yi取对应类别时为1)加入l2正则化:J(W,b)=−1n∑i=1n∑k=1KI(yi=k)logp(yi|xi,w,b)+λ2∑i=1n∑k=1K||wi,j||22 J ( W , b ) = − 1 n ∑ i = 1 n ∑ k = 1 K I ( y i = k ) l o g p ( y i | x i , w , b ) ( I 为 指 示 函 数 , y i 取 对 应 类 别 时 为 1 ) 加 入 l 2 正 则 化 : J ( W , b ) = − 1 n ∑ i = 1 n ∑ k = 1 K I ( y i = k ) l o g p ( y i | x i , w , b ) + λ 2 ∑ i = 1 n ∑ k = 1 K | | w i , j | | 2 2 - 梯度下降
与二项逻辑回归的梯度下降类似:
∂J(W,b)∂W∂J(W,b)∂bW−b−=−1n∑i1σ(yi;xi)σ(yk;xi)(δi,j−σ(yi;xi))xi(参考前面的softmax求导)=−1n∑i(δi,k−σ(yi;xi))xi=−1n∑iδi,k−σ(yi;xi)(这里的δi,k表示的是对于样本i是否被正确分类)=−∂J(W,b)∂W=−∂J(W,b)∂b(达到迭代伦次或者损失函数降到阈值以下停止) ∂ J ( W , b ) ∂ W = − 1 n ∑ i 1 σ ( y i ; x i ) σ ( y k ; x i ) ( δ i , j − σ ( y i ; x i ) ) x i ( 参 考 前 面 的 s o f t m a x 求 导 ) = − 1 n ∑ i ( δ i , k − σ ( y i ; x i ) ) x i ∂ J ( W , b ) ∂ b = − 1 n ∑ i δ i , k − σ ( y i ; x i ) ( 这 里 的 δ i , k 表 示 的 是 对 于 样 本 i 是 否 被 正 确 分 类 ) W − = − ∂ J ( W , b ) ∂ W b − = − ∂ J ( W , b ) ∂ b ( 达 到 迭 代 伦 次 或 者 损 失 函 数 降 到 阈 值 以 下 停 止 )
参考
- 英文维基百科词条,losistic函数
- 英文维基百科词条,sigmoid函数
- 英文维基百科词条,softmax函数
- 英文维基百科词条,交叉熵
- 斯坦福大学深度学习教程,Softmax Regression
- 周志华,机器学习
- 李航,统计学习方法





 本文详细介绍了逻辑回归,包括sigmoid函数的数学概念、性质和导数,以及在二项逻辑回归中的应用。此外,还探讨了softmax函数,它是sigmoid的泛化,用于解决多分类问题。通过数学建模和梯度下降,展示了从二分类到多分类的逻辑回归过程。
本文详细介绍了逻辑回归,包括sigmoid函数的数学概念、性质和导数,以及在二项逻辑回归中的应用。此外,还探讨了softmax函数,它是sigmoid的泛化,用于解决多分类问题。通过数学建模和梯度下降,展示了从二分类到多分类的逻辑回归过程。
















 2754
2754

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








