语言模型总结（待完善）

1. 基本概念

1.1语言模型的概念

生成文本序列的通常方式是训练模型在给定所有先前词／字符的条件下预测下一个词／字符出现的概率。此类模型叫作统计语言模型.
任意语言模型的主要目的都是学习训练文本中字符／单词序列的联合概率分布，即尝试学习联合概率函数。从而捕捉训练文本的统计结构。

记$W=w_1^K=(w_1,...,w_K)$表示由K个词$w_1,...,w_K$按顺序构成的一个句子。则这个句子的概率为$$\begin{gathered} P(W)=P(w_1^K)=P(w_1,...,w_K)//联合概率 \\ =P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)\dots P(w_K|w_1,w_2,...,w_{K-1}) \\ =P(w_1)P(w_2|w_1^1)P(w_3|w_1^2)...P(w_K|w_1^{K-1})//记为向量形式 \\ =\prod _{i}P(w_i|w_1^{i-1}) \end{gathered}$$

1.2马尔可夫假设

一个词出现的概率只与它前面的n-1个词有关
$$P(w_i|w_1^{i-1})\approx P(w_i|w_{i-n+1}^{i-1})$$
因此:
$$\begin{gathered} P(W)=P(w_1^K)=P(w_1,...,w_K) \\ =P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)\dots P(w_K|w_1,w_2,...,w_{K-1}) \\ \approx \prod _{i}P(w_i|w_{i-n+1}^{i-1})//马尔可夫n元假设 \\ \approx P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)\dots P(w_n|w_{n-2},w_{n-1})//马尔可夫三元假设 \\ \approx P(w_1)P(w_2|w_1)P(w_3|w_2)...P(w_n|w_{n-1})//马尔可夫假设二元模型 \end{gathered}$$由大数定理，概率用频率近似:$$P(w_i|w_{i-1})=\frac{P(w_{i-1},w_i)}{P(w_{i-1})}\approx \frac{count(w_{i-1},w_i)}{count(w_{i-1})}$$

1.3语言模型的目标函数

极大似然法$$\begin{gathered} max\prod _{w\in \mathcal{C}}P(w|Context(w)) \\ =\sum _{w\in \mathcal{C}}logP(w|Context(w)) \end{gathered}$$
其中$Context(w)$等价于上面的$w_{i-n+1}^{i-1}$

1.4语言模型的评价指标

1.4.1实用方法

通过查看该模型在实际应用（如拼写检查、机器翻译）中的表现来评价

• 优点：直观、实用
• 缺点：缺乏针对性、不够客观

1.4.2理论方法：困惑度（preplexity）

• 基本思想：给测试集的句子赋予较高概率值的语言模型较好,当语言模型训练完之后，测试集中的句子都是正常的句子，那么训练好的模型就是在测试集上的概率越高越好
• 公式表示：
  

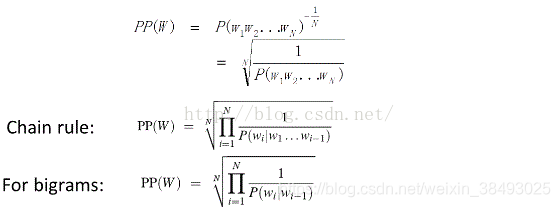
2. n元语法模型（n-gram）

由于n-gram语言模型的优异性能和高效实现，其作为统治性的语言建模方法已经有数十年了。

2.1缺点：

• 一是数据稀疏性，鲁棒性参数估计需要复杂的平滑技术。
• 二是在于n阶马尔科夫假设，预测的词概率值依赖于前n-1个词，这样更长距离上下文依赖就被忽略了。

3. 循环神经网络语言模型（RNNLMs）

RNNLMs将每个词映射到一个紧凑的连续向量空间，该空间使用相对小的参数集合并使用循环连接来建模长距离上下文依赖。
从而RNNLMs就为n-gram的两个关键问题提供了解决方案。并且，RNNLMs在语音识别任务中相对于n-gram语言模型表现出了重大的提升，这导致了其大范围的应用。

3.1缺点：

• 训练RNNLMs对计算量要求苛刻
• 处理大量数据时缓慢的训练速度限制了RNNLMs的使用。

4. 长短期记忆网络（LSTM）

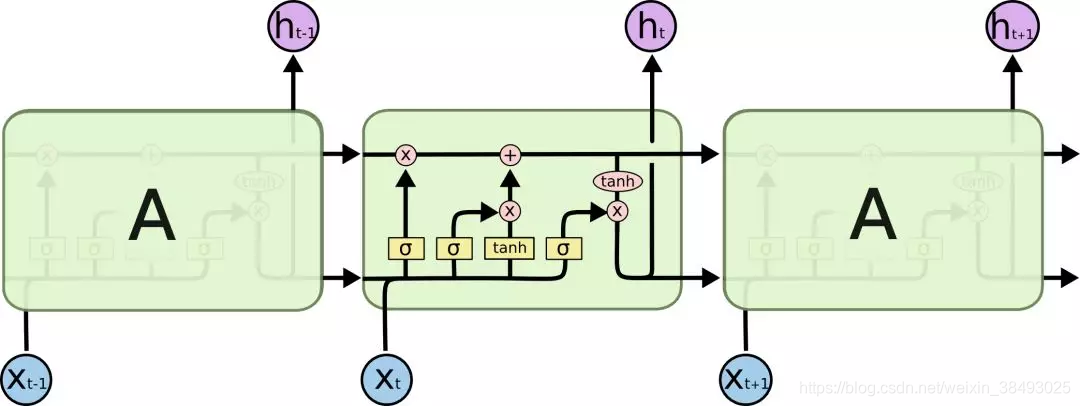
4.1优点：

使用LSTM模型可以更好的捕捉到较长距离的依赖关系。因为LSTM通过训练过程可以学到记忆哪些信息和遗忘哪些信息。

4.2缺点：

利用LSTM对句子进行建模时无法编码从后到前的信息

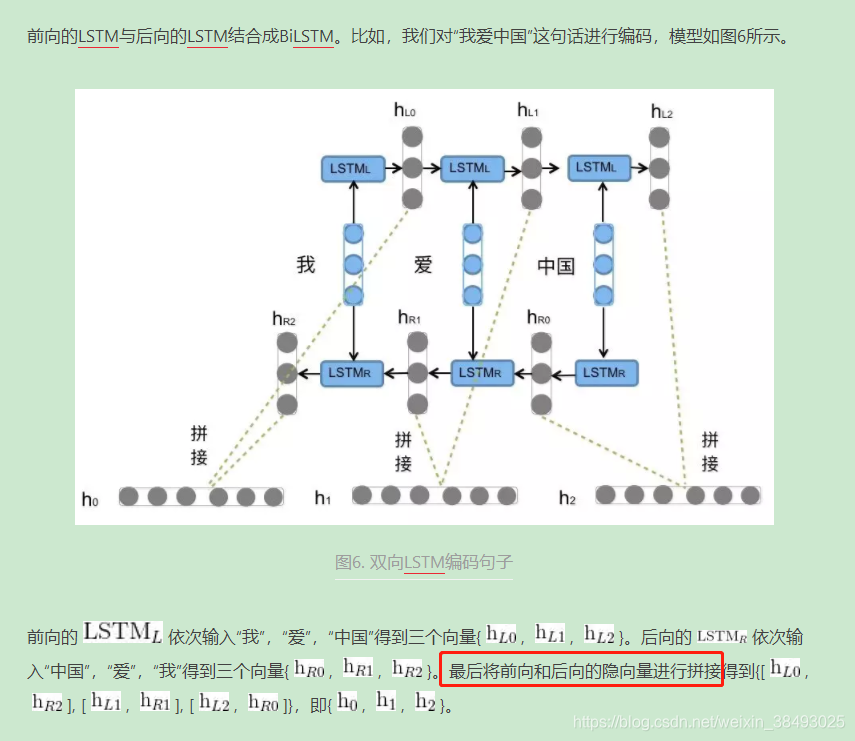
5. 双向长短期记忆网络（BiLSTM）

通过BiLSTM可以更好的捕捉双向的语义依赖。

参考资料：

• 从字符级的语言建模开始，了解语言模型与序列建模的基本概念
  https://baijiahao.baidu.com/s?id=1597625921226025278&wfr=spider&for=pc