Python之高等数学（导数的性质，切线法，二分法）

函数的单调性
定理：设函数 y = f (x) 在 [a, b] 上连续，在 (a, b) 内可导 .
如果在 (a, b) 内 f ' (x) ≥ 0, 且等号仅在有限多个点处成立，那么函数 y=f(x)在 [a,b]上单调增加；

 如果在 (a, b) 内 f ' (x) ≤ 0, 且等号仅在有限多个点处成立，那么函数 y=f(x)在 [a,b]上单调减少；

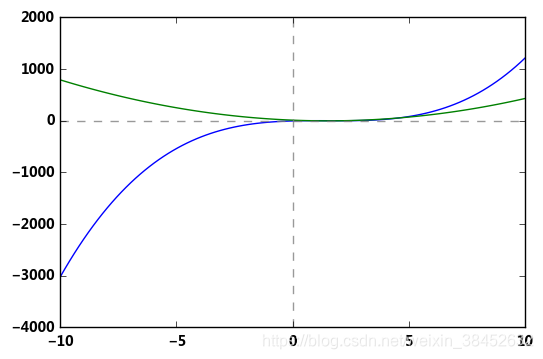
# f(x) = 2*x**3 - 9*x**2 + 12*x - 3

def f1(x):
    return 2*x**3 - 9*x**2 + 12*x - 3   # 函数
def f1_1(x):
    return 6*x**2 -18*x + 12

n = np.linspace(-10,10,num = 100)
plt.plot(n,f1(n))
plt.plot(n,f1_1(n))

plt.axvline(0,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axhline(0,color = 'gray',linestyle = '--',alpha=0.8)  
# 辅助线

# 结论：设函数y = f(x)在[a,b]上连续，在(a,b)内可导 → 若函数导数始终大于等于0，该函数单调增加；反之单调减少

曲线的凸凹性
定理：设函数 y = f (x) 在 [a, b] 上连续，在 (a, b) 内具有一阶和二阶导数，那么
 如果在 (a, b) 内 f '' (x) > 0, 则函数 y=f(x)在 [a,b]上是凹的；
 如果在 (a, b) 内 f '' (x) < 0, 则函数 y=f(x)在 [a,b]上是凸的；

# 二阶导数

def f1_2(x):
    return 12*x - 18

n = np.linspace(-10,10,num = 100)
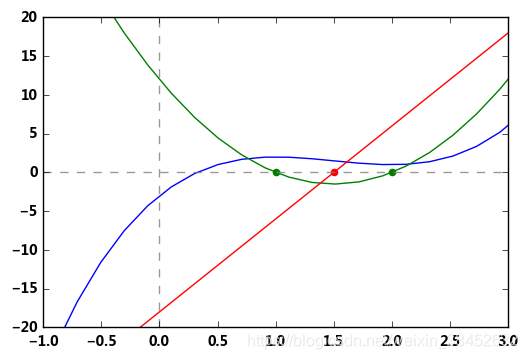
plt.plot(n,f1(n))
plt.plot(n,f1_1(n))
plt.scatter([1,2],[0,0],color = 'green')
plt.plot(n,f1_2(n))
plt.scatter([1.5],[0],color = 'red')

plt.xlim([-1,3])
plt.ylim([-20,20])
plt.axvline(0,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axhline(0,color = 'gray',linestyle = '--',alpha=0.8)  
# 辅助线

# 结论：设函数y = f(x)在[a,b]上连续，在(a,b)内具有一阶和二阶导数 → 若函数二阶导数始终大于等于0，该函数在[a,b]上是凹函数；反之则是凸函数

二分法
设函数 f(x) 在区间 [a,b]上连续， f(a)*f(b)<0,且方程 f(x)=0在 (a,b)内仅有一个实根 ξ,于是 [a,b]即是这个根的一个
隔离区间。
◼ 取 [a, b] 的中点 ξ1 = a + b2，计算 f(ξ1).
 如果 f(ξ1) = 0, 那么 ξ = ξ1,计算结束；
 如果 f(ξ1) 与 f(a) 同号，那么取 a1 = ξ1, b1 = b, 由 f(a1)* f (b1) < 0, 即知 a1 < ξ < b1, 且 b1 - a1 = 12(b - a)；
 如果 f(ξ1) 与 f(b) 同号，那么取 a1 = a, b1 = ξ1, 同理 a1 < ξ < b1, 且 b1 - a1 = 12(b - a)；
◼ 总之，当 ξ ≠ ξ1 时，可求得 a1 < ξ < b1，且 b1 - a1 = 12(b - a)
 

# 二分法求解
# 对于函数f(x) = x**3 + 1.1*x**2 + 0.9*x -1.4
# 单调递增

def f2(x):
    return x**3 + 1.1*x**2 + 0.9*x -1.4
def f2_1(x):
    return 3*x**2 + 2.2*x + 0.9

n = np.linspace(-10,10,num = 100)
plt.plot(n,f2(n))
plt.plot(n,f2_1(n))
plt.axvline(0,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axhline(0,color = 'gray',linestyle = '--',alpha=0.8)  
# 辅助线

print('f(0)和f(1)的值分别为%.2f,%.2f' % (f2(0),f2(1)))
# f(0)=-1.4<0,f(1)=1.6>0,因此f(x)=0在[0,1]内有唯一实根

# 二分法求解

lst = [0,1]
n = 0
while n < 30:
    z = (lst[0]+lst[1])/2
    if f2(z)*f2(0) > 0:   # 即与f(0)同号
        lst[0] = z
    else:
        lst[1] = z    
    print('第%i次迭代的隔离区间为' % (n+1),lst)
    n += 1

第30次迭代的隔离区间为 [0.6706573106348515, 0.670657311566174]

切线法
设函数 f(x) 在区间 [a,b]上具有二阶导数连续， f(a)*f(b)<0,且 f’(x)及 f’’(x)在 [a,b]上保持定号 .这样方程 f(x)=0在
(a,b)内仅有一个实根 ξ,于是 [a,b]即是这个根的一个隔离区间。此时图形仅以下几种情况：
考虑用曲线弧的端点的切线来代替曲线弧，从而求出方程实根的近似值。这种方法叫做切线法
以 f(a)<0,f(b)>0,f’(x)>0,f’’(x)>0讨论令 x0 = b, 在端点 (x0, f (x0)) 处做切线，切线方程为 y - f (x0) = f ' (x0) (x - x0),
得到与 x轴交点 (x1， 0) = x0 - f (x0)f ' (x0), 0 , 它比 x0 更接近方程的根 ξ；在点 (x1, f (x1)) 处做切线，可得到根的近似值 x2;
 如此继续，一般地，在点 (xn, f (xn)) 处作切线，得到根的近似值 xn+1 = xn f (xn)f ' (xn)
 

# 切线法求解
# f ''(x) = 6 x + 2 经判断在区间[0, 1] f '(x)> 0, f ''(x)> 0, 因此f(x) = 0 至多一个实根。

def f2_2(x):
    return 6*x + 2.2

xmin = -0.2
xmax = 1.2
n = np.linspace(xmin,xmax,num = 100)
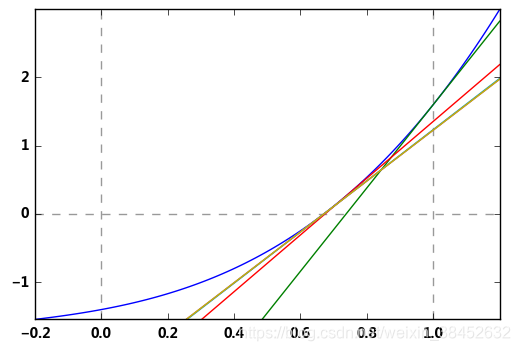
plt.plot(n,f2(n))
plt.xlim([xmin,xmax])
plt.ylim([f2(xmin),f2(xmax)])
plt.axvline(0,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axvline(1,color = 'gray',linestyle = '--',alpha=0.8)  
plt.axhline(0,color = 'gray',linestyle = '--',alpha=0.8)  
# 辅助线

xn = 1
lst_k = []
for i in range(5):
    def f2_qx(xi):
        # 切线函数
        k = f2_1(xn)
        b = f2(xn) - k*xn
        return k*xi + b
    plt.plot(n,f2_qx(n))
    xn = xn - f2(xn)/f2_1(xn)
    print('第%i次迭代的近似值为'%i, xn)