Unity插值详解-优快云博客

Mathf、Vector2、Vector3等许多类都有插值方法。以Vector3为例：

MoveTowards

函数原型为：

public static Vector3 MoveTowards(Vector3 current, Vector3 target, float maxDistanceDelta);

作用是将当前值current移向目标target。（对Vector3是沿两点间直线）
maxDistanceDelta就是每次移动的最大长度。
返回值是当current值加上maxDistanceDelta的值，如果这个值超过了target，返回的就是target的值。

例子：

//表示以每秒moveMax的速度从Current移动到Target。
//因为Current和Target距离是4，所以当moveMax 等于0.5f，用时8秒，moveMax等于2时，用时2秒。
Vector3 Current  = new Vector3(0, 0, 0);
Vector3 Target = new Vector3(0, 0, 4);
Current = Vector3.MoveTowards(Current, Target, moveMax * Time.deltaTime);

Lerp

函数原型为：

public static Vector3 Lerp(Vector3 a, Vector3 b, float t);

它的作用就是按照t计算a和b之间的插值。t的取值范围是[0, 1]。
简单理解就是当t=0，返回值是a，当t=1，返回值是b。同理，t=0.1时是a到b的10%。t就代表了a到b的百分比。

线性插值图示
例1：

//在time时间内移动物体
private IEnumerator MoveObject(Vector3 startPos, Vector3 endPos, float time)
{        
        var dur = 0.0f;
        while (dur <= time)
        {
            dur += Time.deltaTime;
            transform.position = Vector3.Lerp(startPos, endPos, dur / time);
            yield return null;
        }
 }

例2：

//以指定速度speed移动物体
private IEnumerator MoveObject_Speed(Vector3 startPos, Vector3 endPos, float speed)
{
        float startTime = Time.time;
        float length = Vector3.Distance(startPos, endPos);
        float frac = 0;
 
        while (frac < 1.0f)
        {
            float dist = (Time.time - startTime) * speed;
            frac = dist / length;
            transform.position = Vector3.Lerp(startPos, endPos, frac);
            yield return null;
        }
}

Slerp

球形插值在Vector3、Quaternion等类都有使用，一般多在Quaternion的旋转操作时使用。

对于Vector3：

public static Vector3 Slerp(Vector3 a, Vector3 b, float t);

这里球形插值与线性插值不同的地方在于，它将Vectors视为方向而不再是点。返回的向量方向，它的角度是根据a和b的角度插值，而它的长度是根据a和b的长度插值。
可以用其模拟太阳的升降变化等操作。

对于Quaternion：

public static Quaternion Slerp(Quaternion a, Quaternion b, float t);

计算a与b的球形插值。
Quaternion的Lerp与Slerp结果都是一样的，Lerp的效率会比Slerp高些，但是当旋转值a和b离得比较远时，Lerp的效果会非常差。

下面进入对这个函数的详细解释。
初识这个函数的同学们对这个函数都不是很理解，既然是球形插值了，那么为什么用这个函数的时候却这么复杂呢，又要找中心点，又要中心点偏移的弄了半天。其实这是从这个函数的实现方法所决定的。咱们还是上例子来看比较清楚。

首先定义两个向量 a(2,1,0); b(-2,1,0); 然后咱们以这两个坐标点和原点来构建一个三角形，如下图所示：
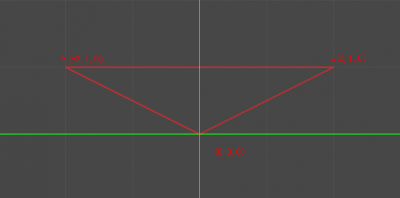
在这里插入图片描述
咱们以a和b两个向量来做插值，假设分10等份，代码比较简单，如下代码

for(inti = 1; i < 10; ++i)
        {
            Vector3 drawVec = Vector3.Slerp(a, b, 0.1f * i);
            Debug.DrawLine(Vector3.zero, drawVec, Color.yellow);
        }

可以看到咱们并没有像官方给的例子那样，做那么多的操作，效果也是杠杠滴！
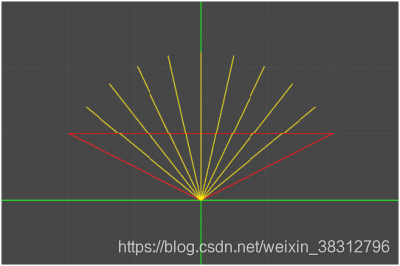
在这里插入图片描述
但是，你不能被表象所欺骗，这样的效果虽然可以，但是却无法控制插值的曲线，也就是那个弧度，虽然你可以调整向量a和向量b的值来调节弧度，比方说a(1,1,0),b(-1,1,0)效果如下，可以看到弧度已经明显变平很多。
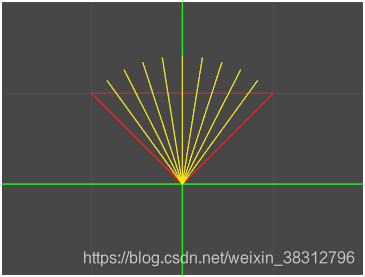
在这里插入图片描述
但是我们在实际运用这个函数的时候往往向量a和向量b是固定的，我们想要的是控制这个弧度，那么怎么办呢，其实也就是改变画这个弧度的中心点位置。上面两个示意图上面中心点我们都是用的坐标原点，我们现在想要在不改变a和a的情况下来改变插值的弧度，就只能自己找出一个中心点，这也就是官方实例中求中心点的由来了。

//弧线的中心
        Vector3 center = (a + b) * 0.5f;
        //我们把中心点向下移动中心，垂直于弧线
        center -= newVector3(0, 0.5f, 0);
        // 求出新的中心点到向量a和向量b的
        Vector3 vecA = a - center;
        Vector3 vecB = b - center;
        for(inti = 0; i <= 10; ++i)
        {
            Vector3 drawVec = Vector3.Slerp(vecA, vecB, 0.1f * i);
            Debug.DrawLine(center, drawVec, Color.yellow);
        }

求出中心点后我们再来画一个示意图看看
在这里插入图片描述
（至于为什么要求出新的中心点到向量a和向量b的vecA和vecB是因为，我们在球形插值的时候要的是两个vector3，而这个vector3是要向量a和向量b到中心点的向量，如果我们不求出vecA和vecB的话不论你怎么插值，其实都是从坐标原点进行的插值，你是控制不了插值的弧度的。）
从上面的效果图我们可以看到插值出来的弧度开始和结束点并不是a、b两点，而是这两个点向下的偏移量，而这个偏移量正好是向量center的负值，所以我们在求出drawVec之后需要对其做修正处理。

在求出drawVec之后加上下面的代码

drawVec += center;

然后再看效果图
在这里插入图片描述
现在的效果图就是我们想要的插值效果了，要想控制弧度，只用调节centor的偏移量就可以了。
比方说我们加上这样一条
center -= new Vector3(0, 2f, 0);
可以看到效果如下

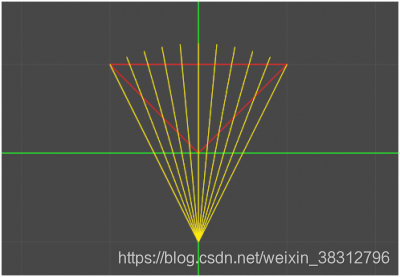
这个弧度是不是就更平了呢。
上面咱们介绍的都是有局限性的，比方说向量a和向量b对于Y轴可是左右对称的，并且X，Y轴的值也是相等的，这在实际运用中可是非常不常见的，现在咱们对向量a做一个比较小的改动看看，把向量a改为(2,1,0),那么效果如下所示
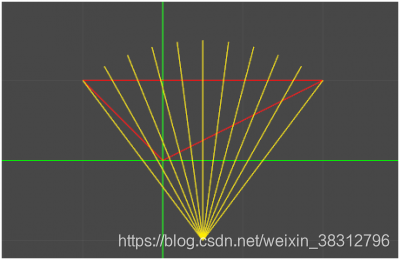
在这里插入图片描述
哇咔咔，居然还是好好的球形插值啊，哈哈，各位同学别激动，咱们把向量a的Y轴也调整一下看看，把a改为（2,4,0）效果如下图所示

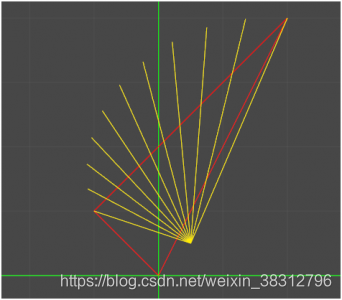
效果是不是非常明显啊，说好的球形插值呢？怎么成了这个样子！！哈哈，各位同学别着急啊，咱们这个球形插值和核心其实就是center点的位置，只要我们求的这个center点的位置在a和b连线中心点的垂线上面，那么就是一个完整的左右对称的插值了。

下面咱们加入如下代码

Vector3 centorProject = Vector3.Project(centor, mStart - mEnd); // 中心点在两点之间的投影
centor = Vector3.MoveTowards(centor, centorProject, 1f); // 沿着投影方向移动移动距离（距离越大弧度越小）

效果如下所示（中心的垂线和起始两条线用蓝色标示出来了）
在这里插入图片描述
所以我们完整的运用Vector3.Slerp的代码应该是这样子滴

//在日出和日落之间动画弧线
usingUnityEngine;
usingSystem.Collections;
 
publicclass example : MonoBehaviour 
{
        publicTransform sunrise;
        publicTransform sunset;
        voidUpdate() 
        {
                //弧线的中心
                Vector3 center = sunrise.position + sunset.position * 0.5f;
                Vector3 centorProject = Vector3.Project(centor, sunrise.position - sunset.position); // 中心点在两点之间的投影
                centor = Vector3.MoveTowards(centor, centorProject, 1f); // 沿着投影方向移动移动距离（距离越大弧度越小）                
                //相对于中心在弧线上插值
                Vector3 riseRelCenter = sunrise.position - center;
                Vector3 setRelCenter = sunset.position - center;
                transform.position = Vector3.Slerp(riseRelCenter, setRelCenter, Time.time);
                transform.position += center;
        }
}

看到这里各位同学是不是觉得已经掌握了Vector3.Slerp了呢？

NONONO！！！！

咱们上面的实例还是有局限性滴，谁告诉你了Vector3的Z轴必须是0了？，咱们对a和b的Z轴在做修改。a（(2, 4, -1)）,b((-1, 1, 2))，看下效果图

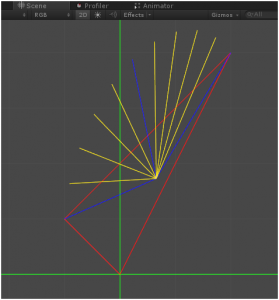
在这里插入图片描述
哇咔咔。。是不是又出问题了？还需要改代码？NO！这是因为我们锁定了视角方向来看的，看上面的2D 选项是不是已经选择了啊，哈哈。那么既然Z轴有值了我们就不能已平面视角来看了，等我们把2D锁定给关闭了转换个视角看看。
在这里插入图片描述
这样看是不是就顺眼多了呢？哈哈，至此我们的讲解总算结束了，大家可以洗洗了，哈哈。。。
等下！谁说可以睡了？我可没说哦，难道大家对我说的都这么信吗？有句古话说的好啊，尽信书则不如无书。。

// 沿着投影方向移动移动距离（距离越大弧度越小）
centor = Vector3.MoveTowards(centor, centorProject, 1f);

在这句代码中我写了个注释（距离越大弧度越小）那么谁能告诉我距离越小会怎么样呢？大家是不是觉得距离越小弧度就越大呢？嘿嘿。。这就掉坑里了吧。
这个距离的小是相对的，尽量是不能小于0.01的，至于为啥是0.01呢，我就试了下0.01和0.001。。。哈哈。。就是这么不负责。。
如果这个距离小于0.01的话插值的方向就是不可控了，至于为什么呢？因为过于小的话就是a到b两点之间的一条线了，垂直于一条线的平面可是海里去了，谁知道在哪里呢。所以大家在用的时候切记这点啊，不能过于追求极限导致结果不可控。还有。。我是不是比较啰嗦啊。。上面我说的是距离啊，是距离，不是值，这个值是可以为负值的啊，负值的话插值的弧线就在这边了，转个向而已。

好了，讲解总算是可以结束了。累死我了。。哇咔咔。。
下面是测试源码，有兴趣的同学玩玩吧

privateVector3 mStart = newVector3(2, 4, -1);
    privateVector3 mEnd = newVector3(-1, 1, 2);
    // Update is called once per frame
    privatevoid Update()
    {
        Debug.DrawLine(newVector3(-100, 0, 0), newVector3(100, 0, 0), Color.green);
        Debug.DrawLine(newVector3(0, -100, 0), newVector3(0, 100, 0), Color.green);
     
     
        Debug.DrawLine(Vector3.zero, mStart, Color.red);
        Debug.DrawLine(Vector3.zero, mEnd, Color.red);
     
        Debug.DrawLine(mStart, mEnd, Color.red);
 
        Vector3 centor = (mStart + mEnd) * 0.5f;
        Vector3 centorProject = Vector3.Project(centor, mStart - mEnd); // 中心点在两点之间的投影
        centor = Vector3.MoveTowards(centor, centorProject, 1f);        // 沿着投影方向移动移动距离（距离越大弧度越小）
 
        Debug.DrawLine(centor, mStart, Color.blue);
        Debug.DrawLine(centor, mEnd, Color.blue);
 
        Debug.Log(string.Format("{0} : {1}", Vector3.Distance(centor, mStart), Vector3.Distance(centor, mEnd)));
 
        for(inti = 1; i < 10; ++i)
        {
            Vector3 drawVec = Vector3.Slerp(mEnd - centor, mStart - centor, 0.1f * i);
            drawVec += centor;
            Debug.DrawLine(centor, drawVec, 5 == i ? Color.blue : Color.yellow);
         }
    }