卷积 、 图像去噪、边缘提取

参考:
https://www.bilibili.com/video/BV1V54y1B7K3?p=8&spm_id_from=pageDriver&vd_source=36b7c8676358c983e1f9ccb9cfe786b4

卷积与图像去噪

图像去噪与卷积

卷积核/卷积模板（带权重的矩阵）

定义：

卷积对图像进行操作

性质

• 叠加性
• 平移不变性
• 交换律
• 结合律
• 分配律
• 标量
  
  边界填充

拉伸
镜像

小结

• 卷积操作后的图像要小于输入时图像，通过边界填充，我们可以实现卷积前后图像的尺寸不变;
• 一种最常用的边界填充就是常数填充。

示例
不变：

平移：

平滑：
锐化：

高斯卷积核

生成步骤：

高斯卷积核

方差越大，平滑越明显

窗宽变化，模板尺寸越大，平滑效果越强

卷积核参数：

3倍方差外，函数值接近0

高斯卷积核 vs 平均卷积核

高斯卷积核

• 丢除图像中的“高频”成分(低通滤波器)
• 两个高斯卷积核卷积后得到的还是高斯卷积核
  • 使用多次小方差卷积核连续卷积，可以得到与大方差卷积核相同
    的结果
  • 使用标准差为α 的高斯核进行两次卷积与使用标准差o√2 的
    高斯核进行一次卷积相同
• 可分离
  • 可分离为两个一维高斯的乘积

卷积操作运算量
1.用尺寸为mm的卷积核 卷积一个尺寸为nn的图像，其计算复杂度是多少
O(n^2 * M^2)
2.

小结
高斯卷积核，能够有效地抑制噪声、实现图像平滑。
高斯卷积核的堆叠以及分解，都可以用于减少卷积计算的复杂度。

图像噪声 与 中值滤波器

噪声

高斯噪声

减少高斯噪声
方差越大，平滑越厉害。
高斯噪声越大，方差越大，但有用的信号也消失了

椒盐噪声、脉冲噪声
使用高斯滤波(线性滤波，加权求和操作），效果不好

中值滤波（排序取中值、不是线性滤波器）


不改变形状

小结：
三种类型的噪声，椒盐噪声、脉冲噪声及高斯噪声。对于前两者建议使用中值滤波器,对于高斯噪声可以使用高斯卷积核来进行去噪。

卷积与边缘提取

边缘:图像中亮度明显而急剧变化的点

为什么要研究边缘?

• 编码图像中的语义与形状信息
• 相对于像素表示，边缘表示显然更加紧凑

边缘检测

图像求导

图像偏导：

图像梯度

梯度mu值 反映 边缘

噪声的影响

真实处理：先平滑再求导

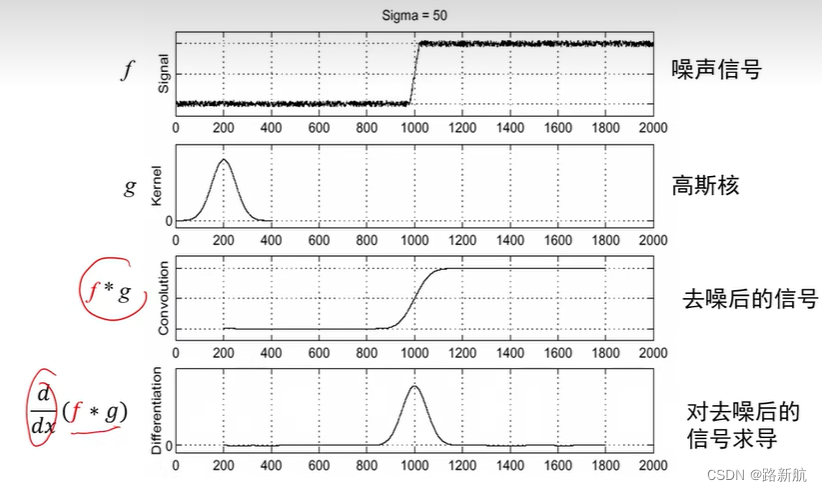
高斯一阶偏导卷积核

小方差关注细微边缘

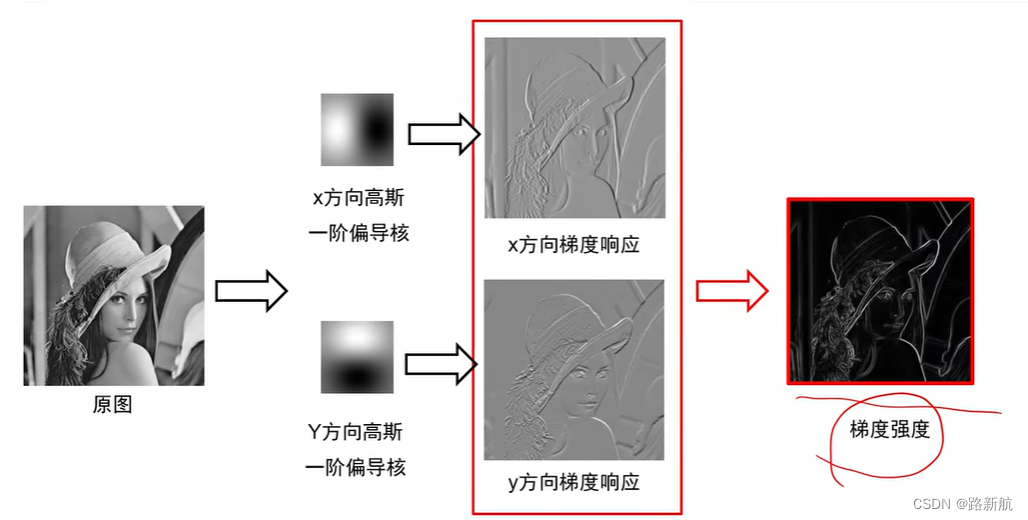
高斯核 vs 高斯一阶偏导核

Canny边缘检测器

非极大值抑制

提示:q点、r点坐标通常不是整数，其对应的强度需要插值获得! ! !

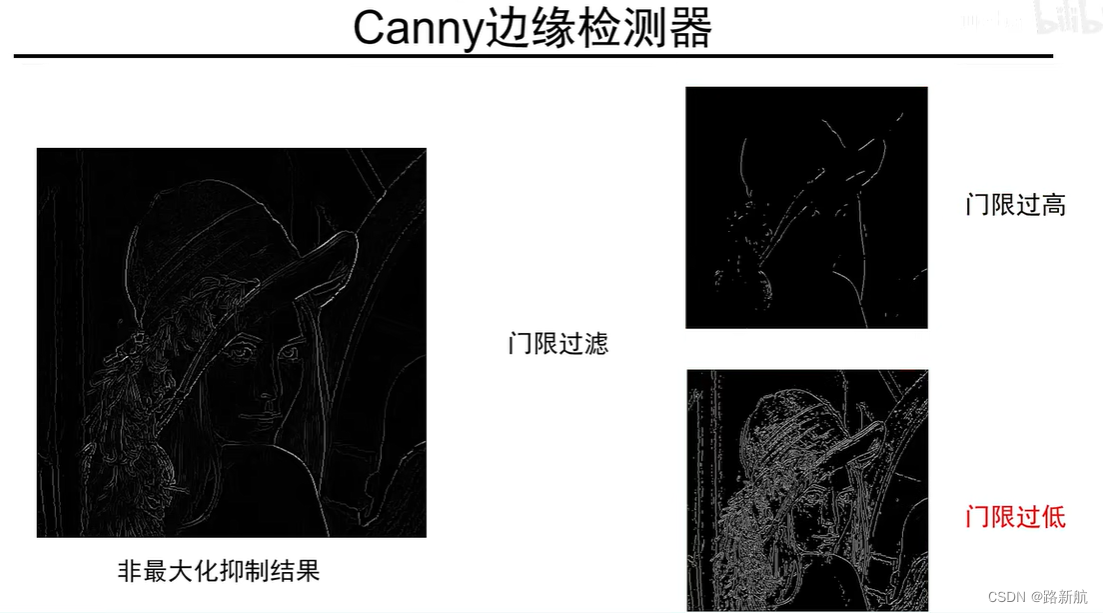
双阈值
保留高阈值边缘，只保留与高阈值有连接的低阈值边

Canny边缘检测器

1. 用高斯一阶偏导核卷积图像
   同时对图像进行去噪和求导
2. 计算每个点的梯度幅值和方向
3. 非极大值抑制:

• 将宽的“边缘”细化至单个像素宽度

4. 连接与阈值（滞后):

• 定义两个阈值:低和高
• 使用高阈值开始边缘曲线，使用低阈值继续边缘曲线

纹理

规则纹理 和 随机纹理

基于卷积核组的纹理表示方法
思路:
利用卷积核组提取图像中的纹理基;
利用基元的统计信息来表示图像中的纹理

卷积核

基于卷积核组的图像表示

纹理分类任务

基元均值表示

白色表示该方向值越大，该核描述的东西越多

卷积核组设计
设计重点:

• 卷积核类型(边缘，条形以及点状)
• 卷积核尺度(3-6个尺度)
• 卷积核方向(6个角度)

高斯一阶偏导 边缘
高斯二阶偏导 条状
提取点状、斑点

sigma越大关注越粗犷的边

例子

每个特征点对应的48维向量很稀疏

卷积神经网络

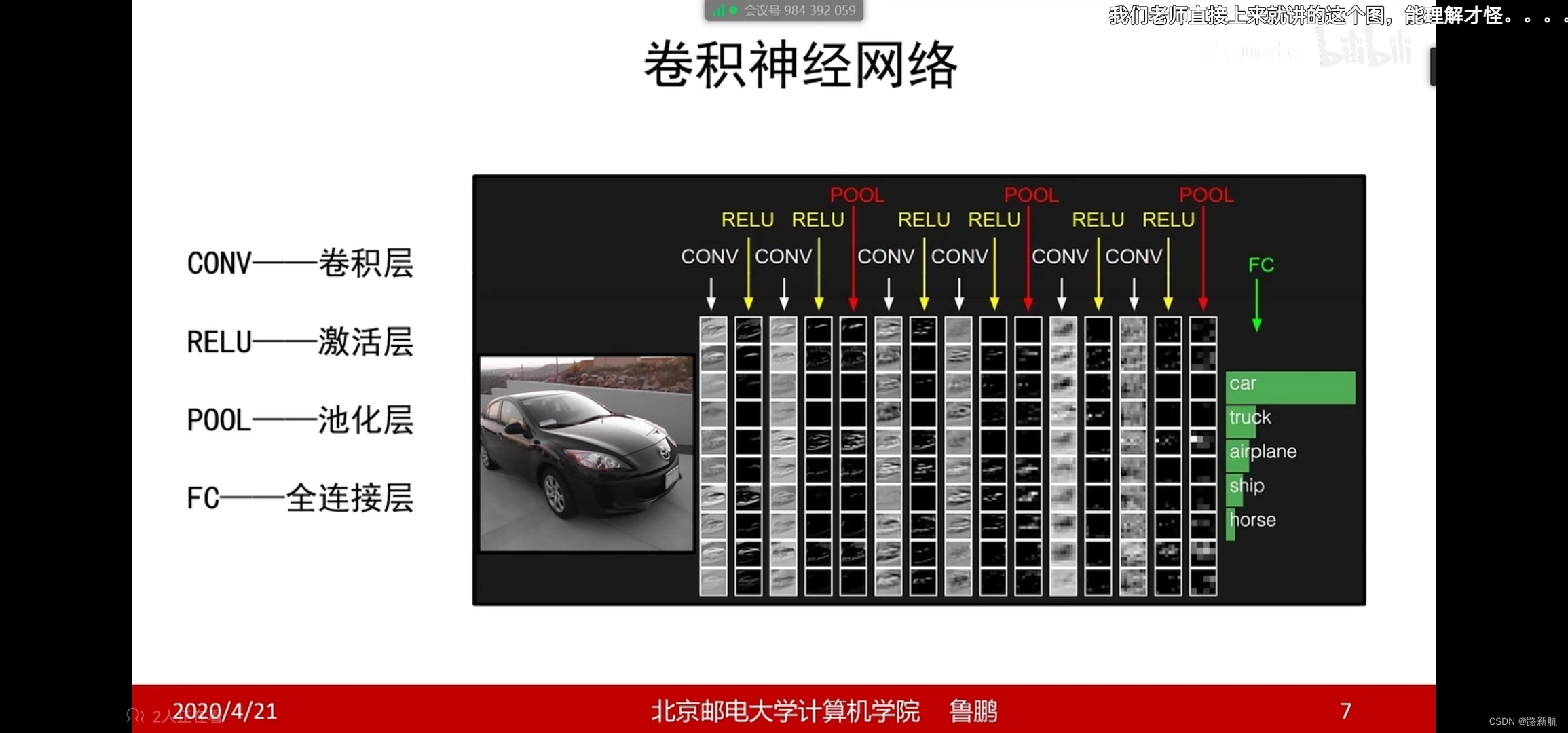
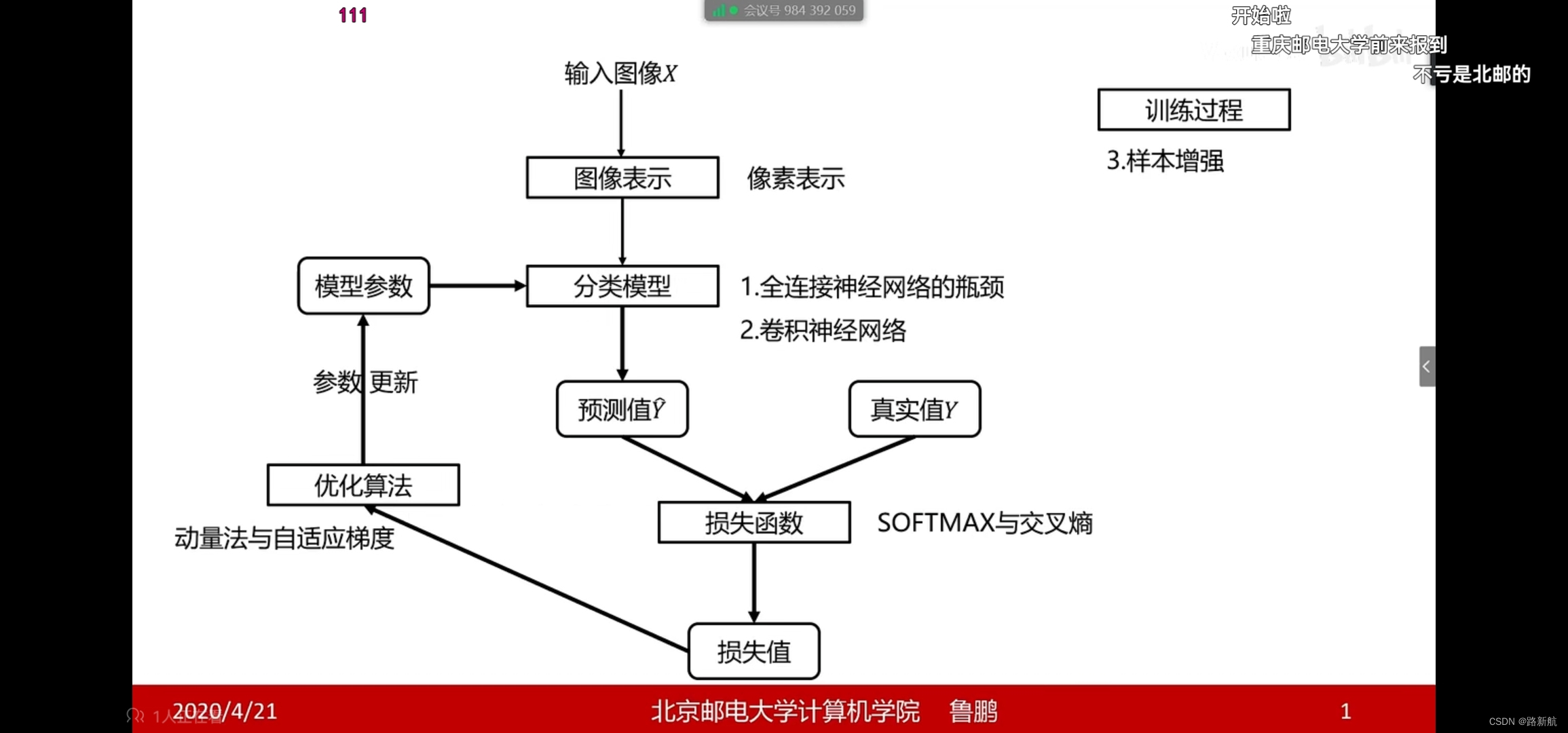
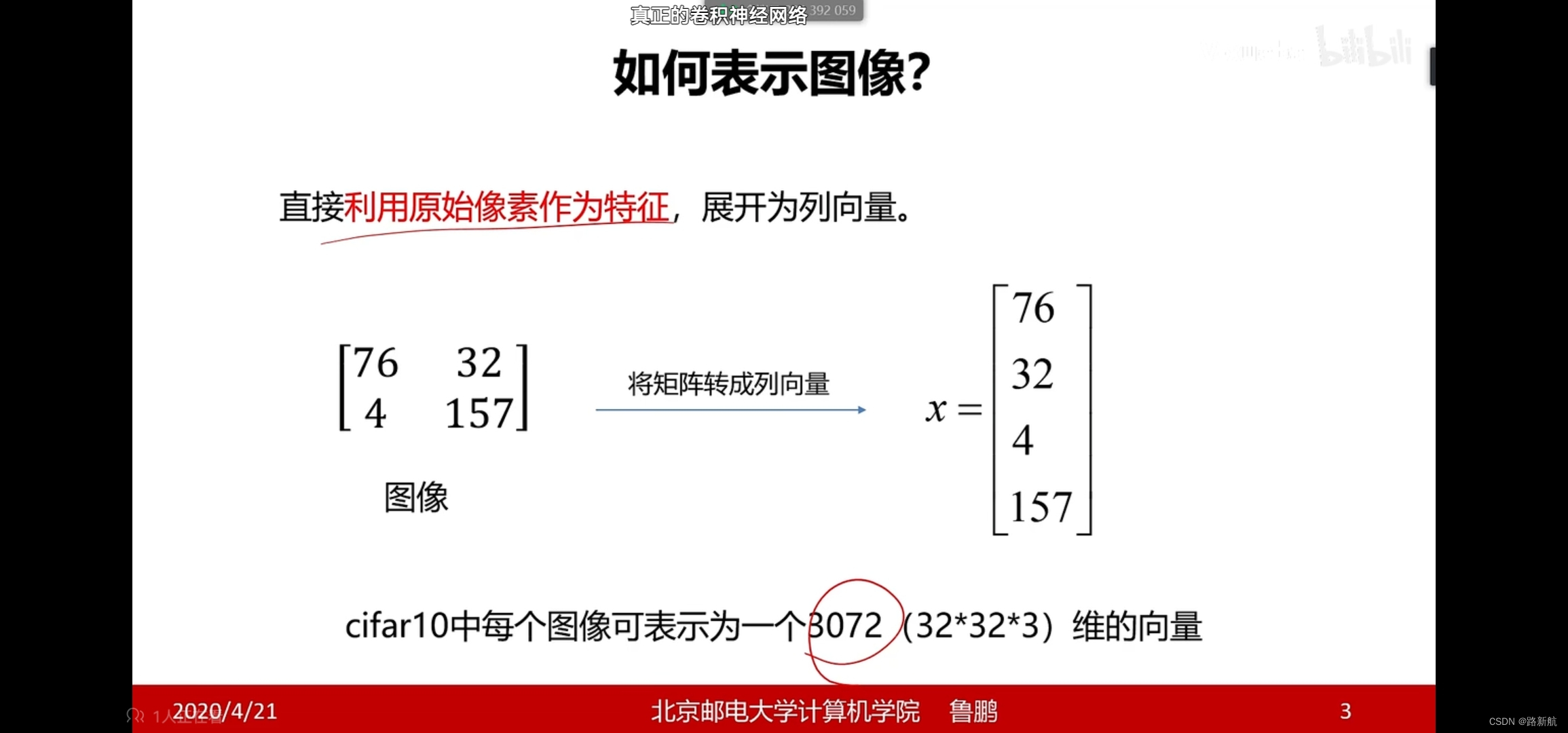
表示图像
利用原始像素作为特征

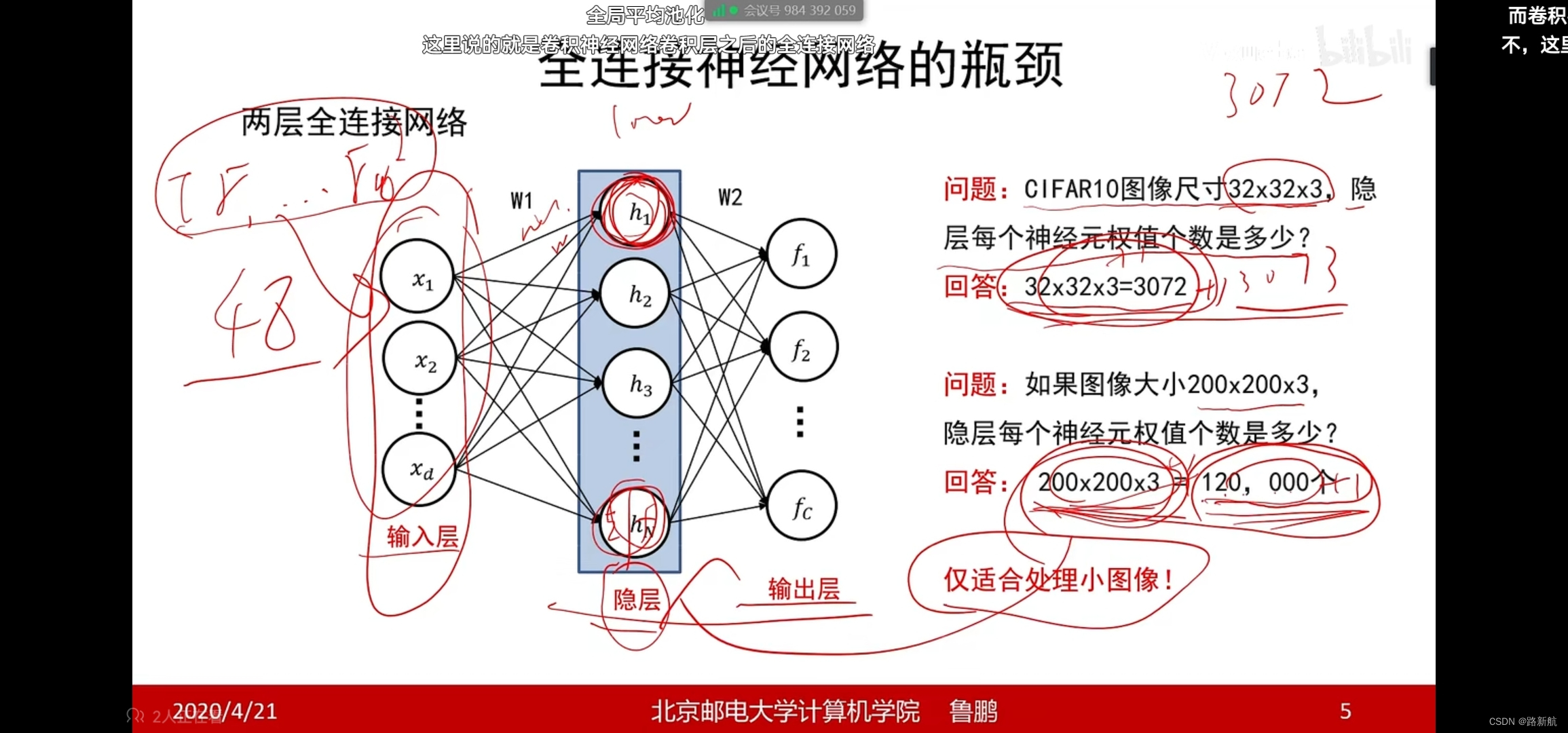
全连接神经网络的瓶颈

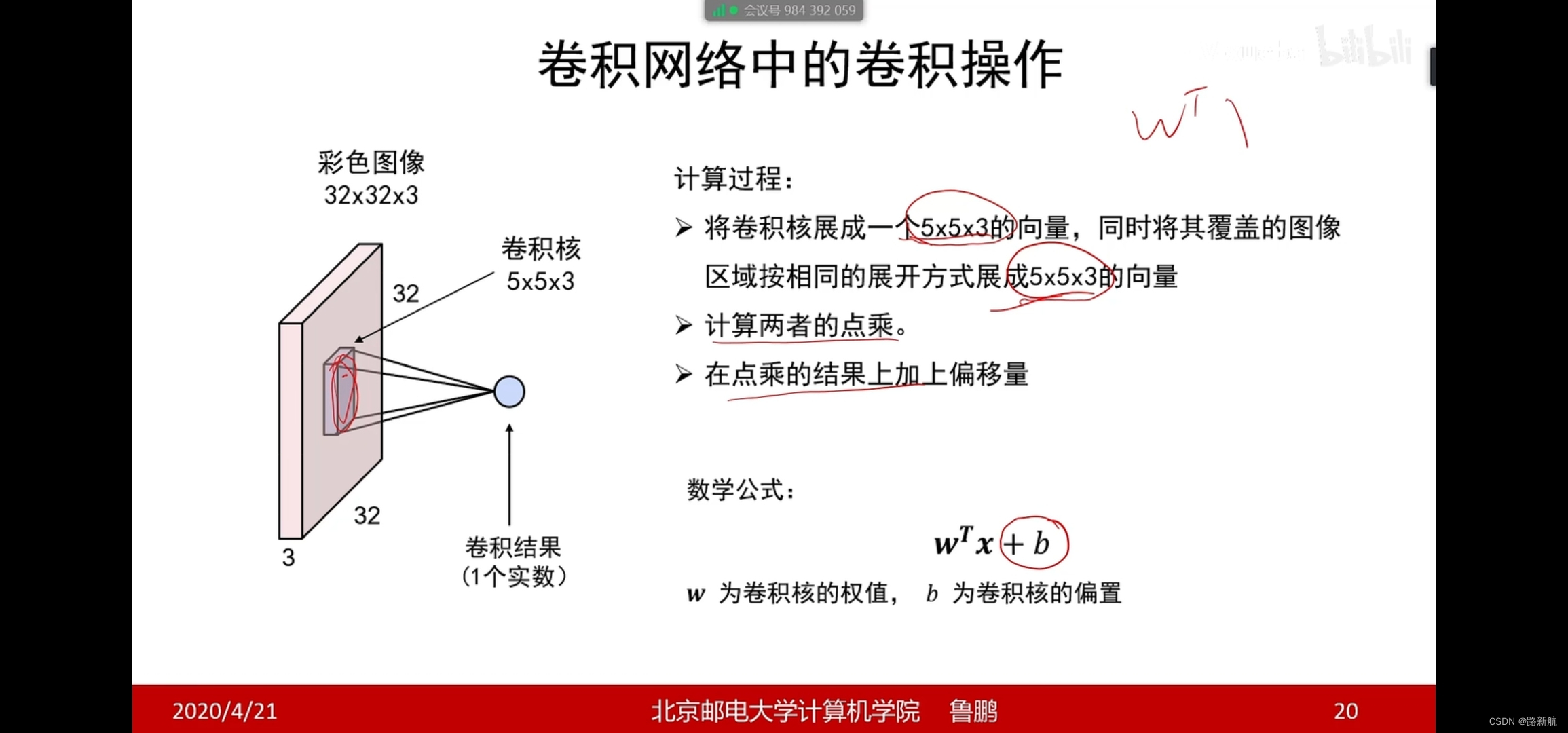
卷积核

卷积操作

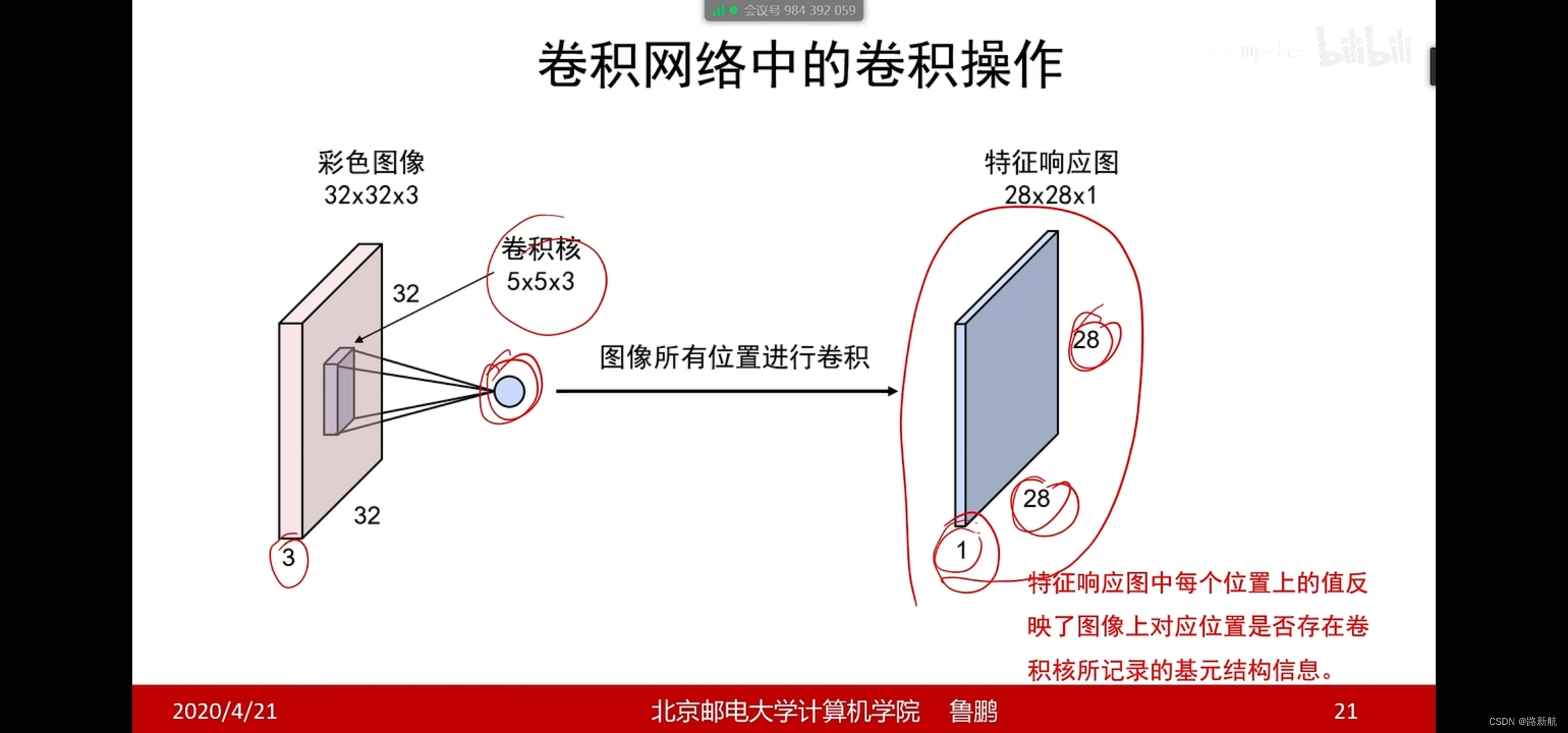
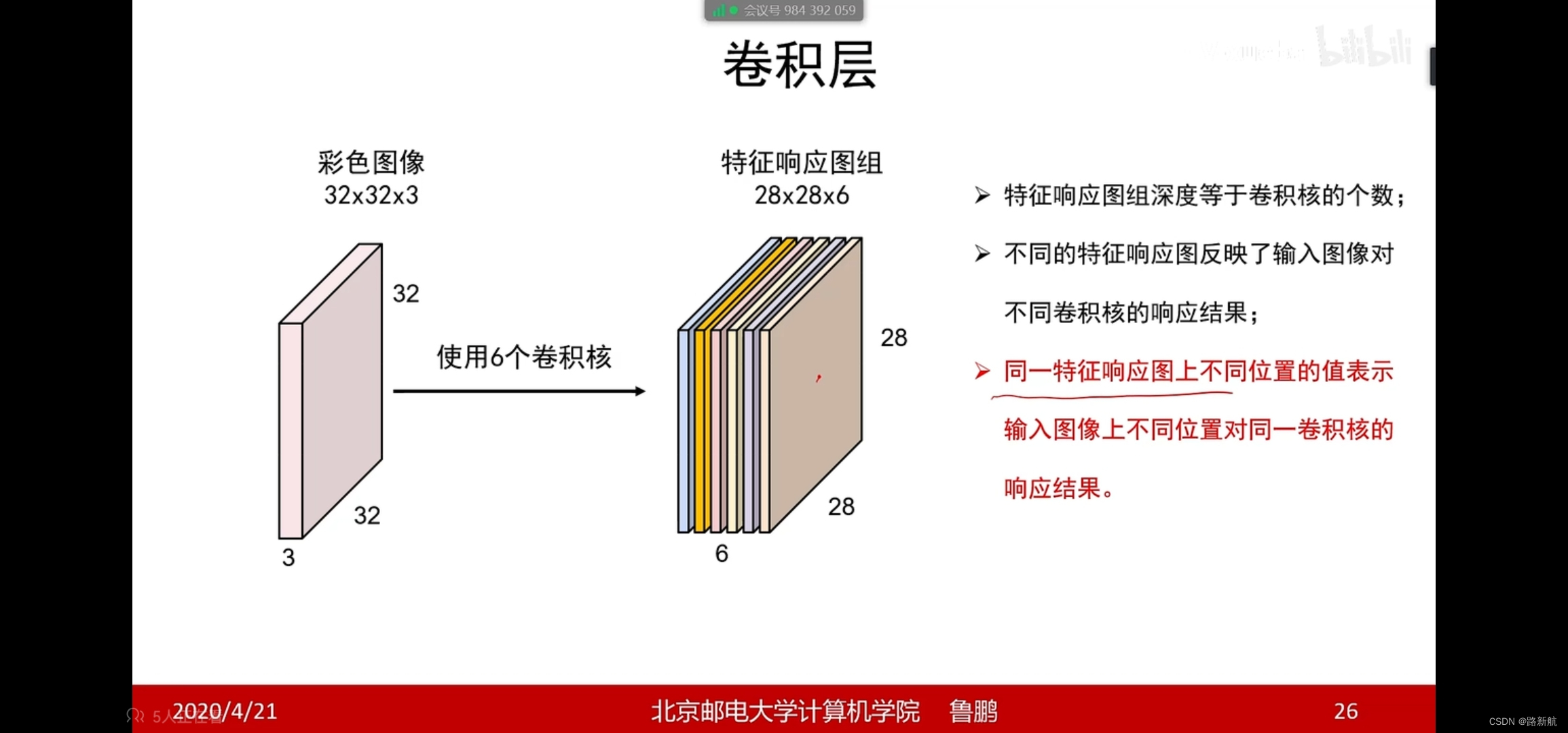
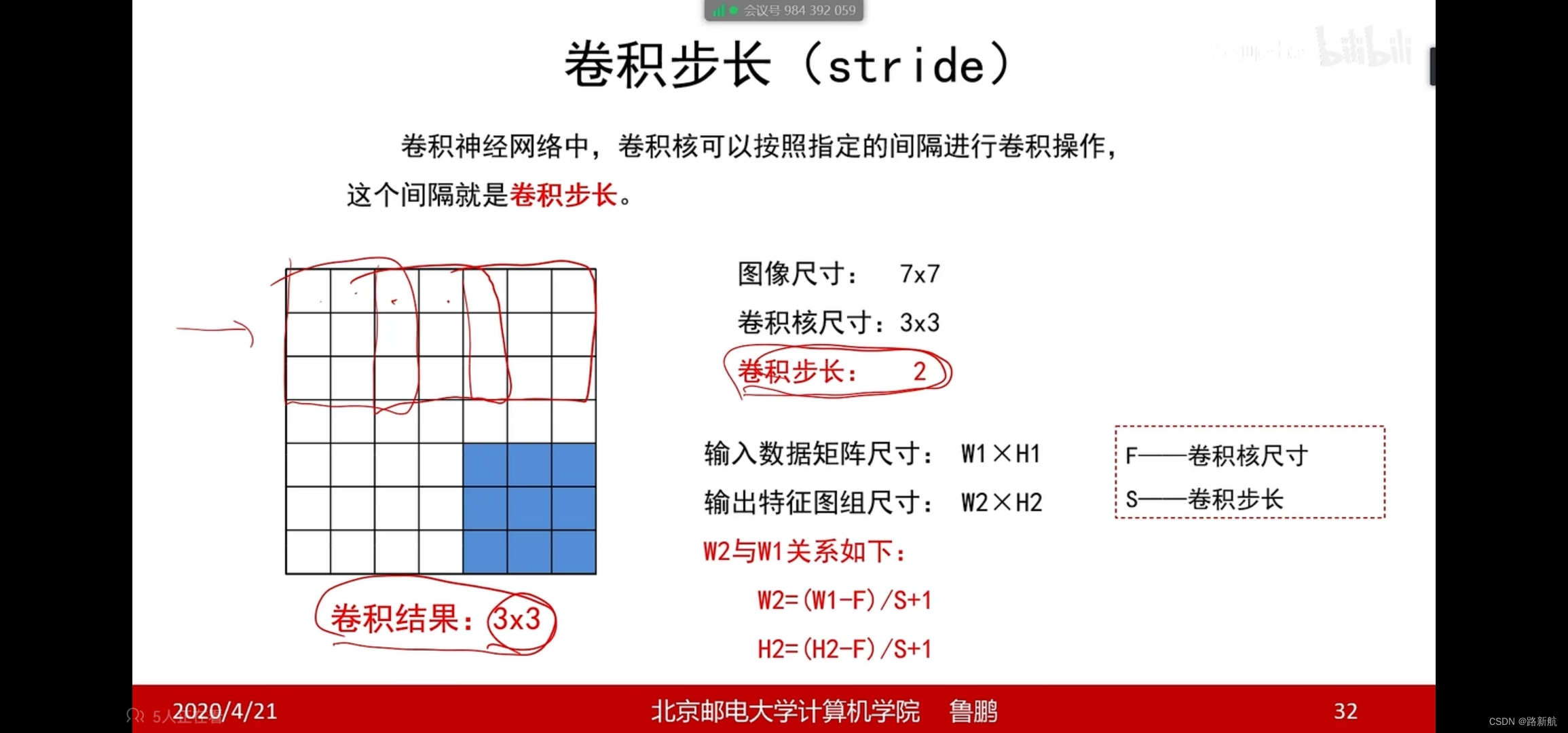
卷积步长

边界填充

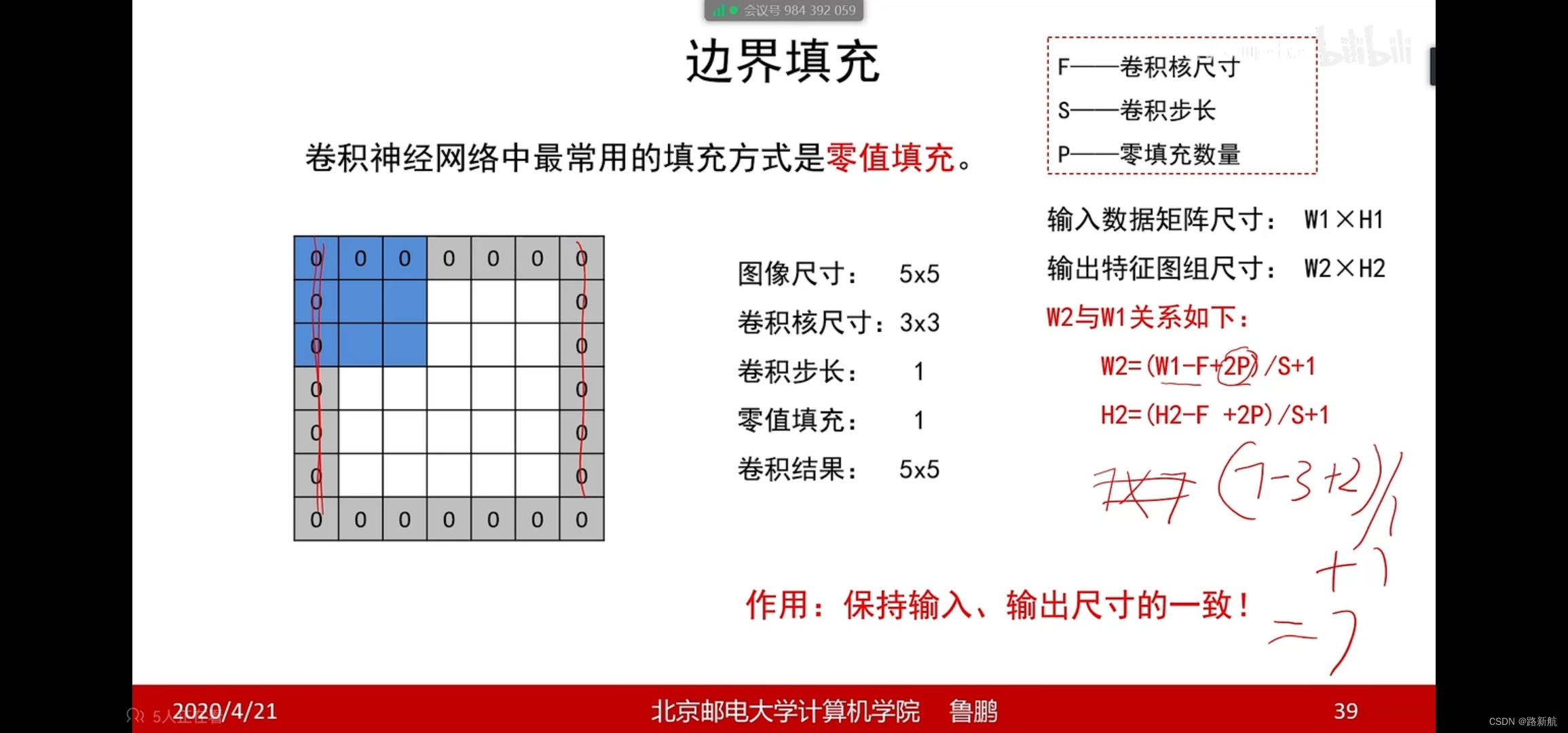
特征图尺寸计算
(W-F+2P)/S+1

池化操作

池化的作用:
对每一个特征响应图独立进行，降低特征响应图组中每个特征响应图的宽度和高度，减少后续卷积层的参数的数量，降低计算资源耗费，进而控制过拟合。

池化操作:对特征响应图某个区域进行池化就是在该区域上指定一个值来代表整个区域。

常见的池化操作:

• 最大池化——使用区域内的最大值来代表这个区域;
• 平均池化——采用区域内所有值的均值作为代表。
  

1.计算量减小
2.增大感受视野（图变小相当于卷积核尺寸变大）
3.非最大化抑制，最重要特性保留

迟化操作示例

损失函数：交叉熵损失
优化算法：SGD 带动量的SGD ADAM

图像增强

• 镜像翻转
• 随机缩放
• 色彩抖动
• 平移
• 旋转
• 拉伸
• 径向畸变（相关描述见摄像机几何章节)
• 裁剪