洛谷P1559 运动员最佳匹配问题（排列树解法和标记数组解法）

题目描述

羽毛球队有男女运动员各n人。给定2 个n×n矩阵P和Q。P[i][j]是男运动员i和女运动员j配对组成混合双打的男运动员竞赛优势；Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响，P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。设计一个算法，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。

输入输出格式

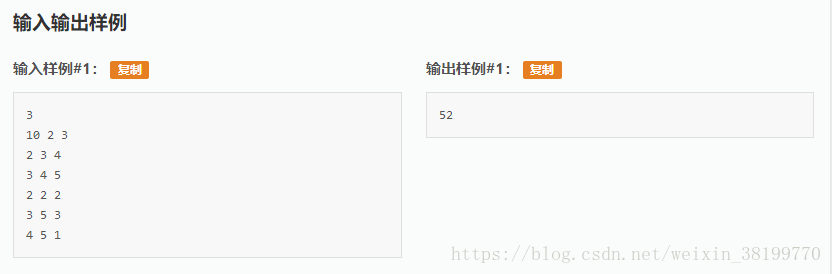
输入格式：

第一行有1 个正整数n (1≤n≤20)。接下来的2n行，每行n个数。前n行是p，后n行是q。

输出格式：

将计算出的男女双方竞赛优势的总和的最大值输出。

解法一：标记数组+可行性剪枝

参考题解：https://www.luogu.org/blog/user21162/solution-p1559

#include<iostream>
#include<algorithm>
using namespace std;
#define INF 0x7ffffff
#define maxn 22
int p[maxn][maxn];
int q[maxn][maxn];
int a[maxn];
int n;
int ans;
bool flag[maxn];

void dfs(int deep,int now)
{
	if (deep >= n+1)
	{
		ans = max(ans, now);
		//cout << ans << endl;
		return;
	}

	int vv = 0; int i;
	for (i = deep; i <= n; i++)
	{
		vv += a[i];
	}
	if (now + vv<ans)return;/////可行性剪枝哦
	for (int i = 1; i <= n; i++)
	{
		if (!flag[i])
		{
			flag[i] = true;
			dfs(deep + 1, now + p[deep][i] * q[i][deep]);
			flag[i] = false;
		}
	}
}

int main()
{
	//freopen("1.txt", "r",stdin);
	cin >> n;
	ans = -INF;
	for (int i = 1; i <= n;i++)
	for (int j = 1; j <= n; j++)
	{
		cin >> p[i][j];
	}

	for (int i = 1; i <= n; i++)
	for (int j = 1; j <= n; j++)
	{
		cin >> q[i][j];
	}

	for (int i = 1; i <= n;i++)
	for (int j = 1; j <= n; j++)
	{
		a[i] = max(a[i], p[i][j] * q[j][i]);
	}
	dfs(1, 0);
	cout << ans;
	return 0;
}

解法二：排列树+分支限界

男运动员位置不动, 女运动员全排列, 回溯搜索最优值

解空间是n的全排列, 所以选择排列树作为解空间结构.

变量设计: 当前得分cs,最佳得分bests, x[1:n]女运动员的排列

定义函数f(i,m,x) = maxj=m+1nP[i][x[j]]*Q[x[j]][i],其中i>m,

是在前m位男运动员已配对的情况下, 男运动员i配对其她女运动员的上界

定义函数Upb(m,x)= f(m+1,m,x)+f(m+2,m,x)+…+f(n,m,x).

当前m位男运动员已配对的情况下, cs+Upb(m,x)是余下情况配对的上界,

由此可以设计剪枝(限制)条件cs+Upb(m,x) > bests 

#include<cstdio>  
#include<cstring>  
#include<climits>  
#include<algorithm>  
#include<stdio.h>
#include<iostream>
#define INF 0x7ffffff
using namespace std;
#define maxn 22
int n;
int p[maxn][maxn];
int q[maxn][maxn];
int x[maxn];
int cw;
int maxValue = 0;

/*
定义函数 f(i,m) = maxj=m+1n P[i][x[j]]*Q[x[j]][i], 其中i>m,
是在前m位男运动员已配对的情况下, 男运动员i配对其她女运动员的上界

*/
int f(int i, int m)
{
	int ans = 0;
	for (int j = m+1; j <= n; j++)
		ans = max(ans,p[i][x[j]]*q[x[j]][i]);
	return ans;
}
/*
定义函数 Upb(m) = f(m+1,m)+f(m+2,m)+…+f(n,m).
当前m位男运动员已配对的情况下, cs+Upb(m)是余下情况配对的上界,
由此可以设计剪枝(限制)条件 cs+Upb(m) > maxValue

*/
int Upb(int m)
{
	int sum = 0;
	for (int i = m+1 ; i <= n; i++)
		sum += f(i, m);
	return sum;
}
void backTrack(int t) {
	if (t > n) 
	{
		maxValue = max(maxValue, cw);
		return;
	}

		for (int i = t; i <= n; i++) 
		{ 
			swap(x[i], x[t]); 
			cw += p[t][x[t]]*q[x[t]][t];
			if (cw + Upb(t) > maxValue)
			{
				backTrack(t + 1);
			}
			cw -= p[t][x[t]] * q[x[t]][t]; //回溯 
			swap(x[t], x[i]);
		}
	
}
int main()
{ 
	cin >> n;
		for (int i = 1; i <= n; i++) 
		{
			for (int j = 1; j <= n; j++) 
			{
				scanf("%d", &p[i][j]); 
			}
		}
		for (int i = 1; i <= n; i++) 
		{
			for (int j = 1; j <= n; j++) 
			{
				scanf("%d", &q[i][j]);  
			}
		}
		for (int i = 1; i <= n; i++)
			x[i] = i;
		backTrack(1);
		printf("%d\n", maxValue); 
		return 0;
}