雅可比矩阵（整理）

而矩阵的行列式的值的几何意义：是矩阵对应的线性变换前后的面积比。

概念：在向量分析中, 雅可比矩阵是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式

          雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数.

 

 

总结一下，雅可比矩阵可以理解为：

若在n维欧式空间中的一个向量映射成m维欧式空间中的另一个向量的对应法则为F，F由m个实函数组成，即：

那么雅可比矩阵是一个m×n矩阵：

 

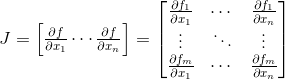
其中输入向量x = (x1, ... , xn)，输出向量y = (y1, ..., ym)，