分类模型评价指标和方法

分类模型评价指标和方法

基本概念

• True negative(TN)，称为真反例，实际是负样本预测成负样本的样本数
• False positive(FP)，称为假正例，实际是负样本预测成正样本的样本数
• False negative(FN)，称为假反例，实际是正样本预测成负样本的样本数
• True positive(TP)，称为真反例，实际是正样本预测成正样本的样本数

T和F表示预测是否正确，P和N表示预测结果是正例还是反例

混淆矩阵

真实情况（斜体）	正例	反例
正例	TP	FN
反例	FP	TN

常见指标

• 准确率
  预测正确的比例$accuracy=\frac{(TP+TN)}{TP+FP+TN+FN}$

• 查准率
  模型预测为正类的样本中，真正为正类的样本所占的比例$precision=\frac{TP}{TP+FP}$

• 召回率（查全率）
  模型正确预测为正类的样本的数量，占总的正类样本数量的比值$recall=\frac{TP}{TP+FN}$

• P-R曲线
  查准率和查全率是一对矛盾的度量，一般来说，查准率高时，查全率往往偏低，查全率高时，查准率往往偏低。查准率-查全率曲线：precision为纵轴，recall为横轴。P-R曲线见下：

如果一个模型的P-R曲线完全包住另一个学习器的P-R曲线，则前一个模型一定更优。如图中的模型A包住了模型C，故模型A优于模型C；B也包住了C，模型B也优于模型C。模型A和模型B有交叉重叠的部分，我们需要比较曲线下方的面积大小，但曲线下方的面积并不容易直接比较。故引入平衡点或者是F1值进行比较。 - 平衡点 平衡点(BEP)是查准率等于查全率时的取值，如果这个值较大，则说明学习器的性能较好。如上图，模型A的平衡点值大于模型B，故模型A优于模型B。

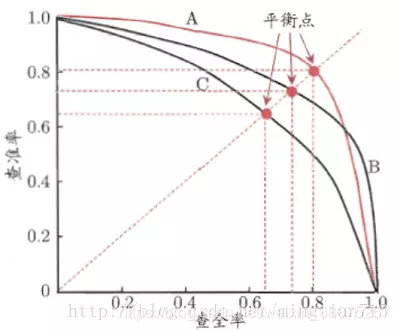
• $F_1$-Score

  • $F_1=\frac{2\ast P\ast R}{P+R}$，同样，F1值越大，我们可以认为该学习器的性能较好。
  • $F_1$其实是查准率和查全率的调和平均,即认为$F_1$中的"1"表示的意义就是查准率和查全率的重要性相同。
    $$\frac{1}{F_1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})$$

• $F_{\beta }-score$

  • $F_{\beta }$是查准率和查全率的加权调和平均。当$0<\beta <1$时,查准率precision影响较大(如用户推荐时,为了尽可能少的打扰用户希望推荐的里面尽可能是用户喜欢的,此时precision较为重要);当$\beta >1$时,查全率recall影响更大(如当检索罪犯信息时,希望所有罪犯均能够被识别出来,此时recall较为重要);当$\beta =1$时,查准率和查全率一样重要即$F_1$。
    $$\begin{gathered} \frac{1}{F_{\beta }}=\frac{1}{1+{\beta }^2}(\frac{1}{P}+\frac{{\beta }^2}{R}) \\ {F}_{\beta }=\frac{(1+{\beta }^2)P\ast R}{({\beta }^2\ast P)\ast R} \end{gathered}$$

  • 调和平均与算数平均以及几何平均相比,更重视较小的值。

ROC曲线

ROC曲线即受试者工作特征曲线 (receiver operating characteristic curve),又称为感受性曲线(sensitivity curve)。横坐标为假正例率(FPR)，纵坐标为真正例率(TPR)。横坐标$FPR=\frac{FP}{FP+TN}$，纵坐标$TPR=\frac{TP}{TP+FN}$。由公式可以看到横纵坐标都在[0,1]之间，所以ROC曲线的面积小于等于1。

• ROC曲线的性质
  • (0,0)：假正例率和真正例率都为0，TP=FP=0，即全部预测成负样本
  • (0,1)：假正例率为0，FP=0，真正例率为1，FN=0，全部完美预测正确
  • (1,0)：假正例率为1，TN=0，真正例率为0，TP=0，全部完美预测错误
  • (1,1)：假正例率和真正例率都为1，FN=TN=0，即全部预测成正样本
  • TPR＝FPR，斜对角线，预测为正样本的结果一半是对的，一半是错的，代表随机分类器的预测效果

ROC曲线在斜对角线以下，则表示该分类器效果差于随机分类器，反之，效果好于随机分类器。期望是ROC曲线尽量位于斜对角线以上，也就是向左上角（0,1）凸，因为(0，1)为完美预测。

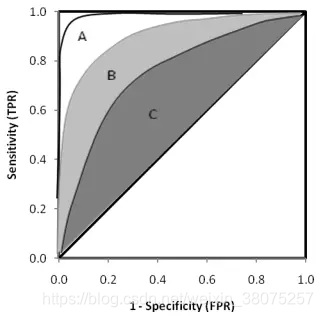
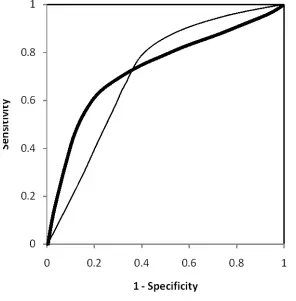
• ROC曲线见下图，当一个模型的ROC曲线完全包裹另一个模型的ROC时，前一个模型更优。如下左图中，A包裹B，B包裹C，则模型A优于模型B，模型B优于模型C。但是对于右图中的两个模型则无法直观的比较哪个更优，故引入AUC曲线。

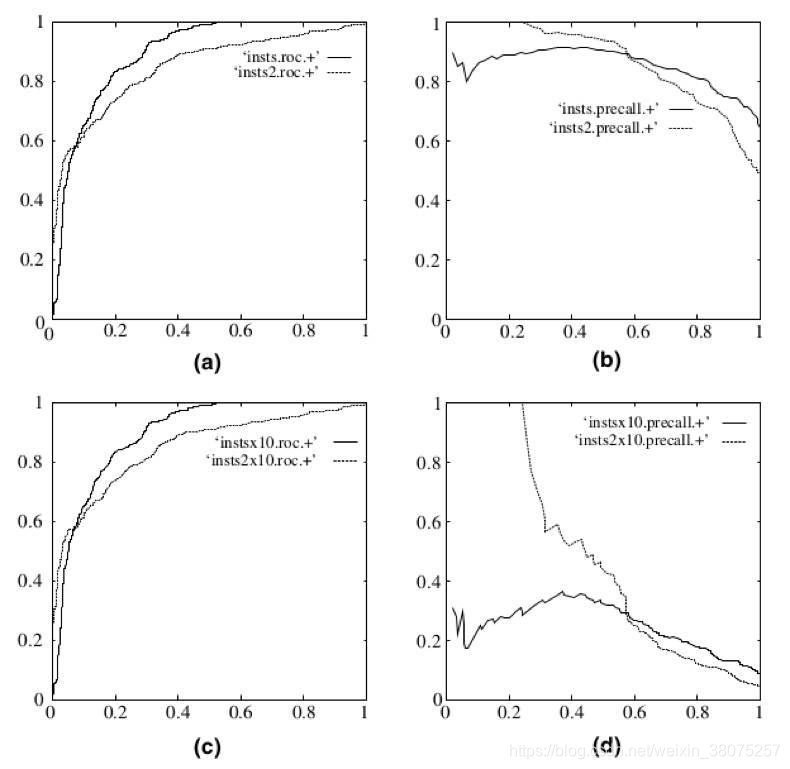
• ROC曲线和PC曲线的区别，ROC更适合用来判断分类效果。因为不会随着正负样本分布变化发生剧烈变化，但是PC曲线可能会随着样本分布发生剧烈变化。作图是ROC曲线，右图是PC曲线，右图的数据是将作图数据里的负样本增加了10倍，可以看到ROC没有发生剧烈变化，但是PC曲线发生了较大的变化。
  

AUC曲线

AUC(Area Under Curve)实际上就是ROC曲线下的面积， AUC直观地反映了ROC曲线表达的分类能力。

• AUC ＝ 1，代表完美分类器
• 0.5 < AUC < 1，优于随机分类器
• 0 < AUC < 0.5，差于随机分类器