机器学习打开01--线性回归_代价函数为联合密度函数-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_37814295/article/details/105643242

线性回归

线性回归的概念
线性回归原理
- 极大似然法
- 极大似然估计（概率角度的诠释）
线性回归损失函数、代价函数、目标函数
线性回归的优化方法
线性回归的评价指标
sklearn.linear_model参数详解：
代码部分
参考

线性回归的概念

1、线性回归的原理
2、线性回归损失函数、代价函数、目标函数
3、优化方法(梯度下降法、牛顿法、拟牛顿法等)
4、线性回归的评估指标
5、sklearn参数详解

线性回归原理

进入一家房产网，可以看到房价、面积、厅室呈现以下数据：

我们可以将价格和面积、厅室数量的关系习得为 $f(x)=\theta_0+\theta_1x_1+\theta_2x_2$ ，使得 $f(x)\approx y$ ，这就是一个直观的线性回归的样式。

线性模型试图学的一个通过属性的线性组合来进行预测的函数
$f(x)=θ_1x_1+θ_2x_2+…θ_nx_n+θ_0$ (一般形式)
向量形式: $f(x)=θ^T+b$ 使得 $f(x_i)≈y$
离散属性的处理：若有“序”，则连续化；否则转换为K维向

式如上，那我们怎么确定 $θ$ 的值呢？这是我问自己的第一个问题

极大似然法

那我们怎么确定 $θ$ 的值呢？这是我问自己的第一个问题
答案如题目所见——极大似然法

什么是极大似然法？
通俗的讲就是利用已知样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。
换句话说，极大似然估计法提供了一种给定观察数据来评估模型参数的方法即“模型已定，参数未知”
我们可以这样想——当模型满足某个分布，它的参数值我们通过极大似然估计法求出来的话。比如正态分布：

$f (x)$ = $\frac{1}{\sqrt {2π}σ}$ exp(- $\frac{(x-μ)^2}{2σ^2}$ )

如果通过极大似然估计，得到模型中的参数μ和σ值，南无这个模型的均值和方差以及其他所有的信息我们是不是就知道了呢，确实是这样。
极大似然法估计采样需要满足一个重要的假设，就是所有的采样都是独立同分布的
https://blog.youkuaiyun.com/u011508640/article/details/72815981?utm_source=app

极大似然估计（概率角度的诠释）

下面我们用极大似然估计，来解释为什么要用均方误差作为性能度量
推导：
（1）假设目标和变量符合如下公式
$f(x)^i=θ^Tx^i+ε^i$

(2) $\epsilon$ 表示我们未观测到的变量的印象，即随机噪音。我们假定 $\epsilon$ 是独立同分布，服从高斯分布。（根据中心极限定理）
$p(ε^i)$ = $\frac{1}{\sqrt {2π}σ}$ exp(- $\frac{(ε^i)^2}{2σ^2}$ )
因此：
$p(y^i|x^i;θ)$ = $\frac{1}{\sqrt {2π}σ}$ exp(- $\frac{(y^i-θ^Tx^i)^2}{2σ^2}$ )
$p(y^i|x^i;θ)$ ：先验概率，在 $x$ 的条件下发生 $y$ 的概率

我们建立极大似然函数，即描述数据遵从当前样本分布的概率分布函数。由于样本的数据集独立同分布，因此可以写成
在这里插入图片描述
此处解释一下独立事件的联合概率：
独立事件，一个事的发生，不影响另一个事件的概率，所以事件A、B独立定义成P(A)=P(A|B），故P(A)= $\frac{P(AB)}{P(B)}$
于是P(AB)=P(A)P(B)
所以上图公式的意义是所有符合在θ条件下，变量为X，值为y的同时发生的概率

选择 $\theta$ ，使得似然函数最大化，这就是极大似然估计的思想。
为了方便计算，我们计算时通常对对数似然函数求最大值：
在这里插入图片描述
这一结果即均方误差，因此用这个值作为代价函数来优化模型在统计学的角度是合理的。
联合密度函数:https://blog.youkuaiyun.com/wys7541/article/details/81056968

线性回归损失函数、代价函数、目标函数

损失函数(Loss Function)：度量单样本预测的错误程度，损失函数值越小，模型就越好。
代价函数(CostFunction)：度量全部样本集的平均误差。
目标函数(Object Function)：代价函数和正则化函数，最终要优化的函数。
常用的损失函数包括：0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等；常用的代价函数包括均方误差、均方根误差、平均绝对误差等。

线性回归的优化方法

梯度下降法

在这里插入图片描述
这个算法成为随机梯度下降法，随机梯度下降法的好处是，当数据点很多时，运行效率更高；缺点是，因为每次只针对一个样本更新参数，未必找到最快路径达到最优值，甚至有时候会出现参数在最小值附近徘徊而不是立即收敛。但当数据量很大的时候，随机梯度下降法经常优于批梯度下降法。

https://blog.youkuaiyun.com/qq_41800366/article/details/86583789?utm_source=app
当J为凸函数时，梯度下降法相当于让参数 $\theta$ 不断向J的最小值位置移动

梯度下降法的缺陷：如果函数为非凸函数，有可能找到的并非全局最优值，而是局部最优值。

最小二乘法矩阵求解

在这里插入图片描述

https://blog.youkuaiyun.com/ccnt_2012/article/details/81127117?utm_source=app

牛顿法

在这里插入图片描述
牛顿法的收敛速度非常快，但海森矩阵的计算较为复杂，尤其当参数的维度很多时，会耗费大量计算成本。我们可以用其他矩阵替代海森矩阵，用拟牛顿法进行估计，

拟牛顿法

在这里插入图片描述

线性回归的评价指标

均方误差(MSE):
在这里插入图片描述
均方根误差(RMSE)

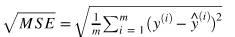
平均绝对误差(MAE)

但以上评价指标都无法消除量纲不一致而导致的误差值差别大的问题，最常用的指标是 $R^2$ ,可以避免量纲不一致问题

我们可以把 $R^2$ 理解为，回归模型可以成功解释的数据方差部分在数据固有方差中所占的比例， $R^2$ 越接近1，表示可解释力度越大，模型拟合的效果越好。

sklearn.linear_model参数详解：

fit_intercept : 默认为True,是否计算该模型的截距。如果使用中心化的数据，可以考虑设置为False,不考虑截距。注意这里是考虑，一般还是要考虑截距

normalize: 默认为false. 当fit_intercept设置为false的时候，这个参数会被自动忽略。如果为True,回归器会标准化输入参数：减去平均值，并且除以相应的二范数。当然啦，在这里还是建议将标准化的工作放在训练模型之前。通过设置sklearn.preprocessing.StandardScaler来实现，而在此处设置为false

copy_X : 默认为True, 否则X会被改写

n_jobs: int 默认为1. 当-1时默认使用全部CPUs ??(这个参数有待尝试)

可用属性：

coef_:训练后的输入端模型系数，如果label有两个，即y值有两列。那么是一个2D的array

intercept_: 截距

可用的methods:

fit(X,y,sample_weight=None): X: array, 稀疏矩阵 [n_samples,n_features] y: array [n_samples, n_targets] sample_weight: 权重 array [n_samples] 在版本0.17后添加了sample_weight

get_params(deep=True)：返回对regressor 的设置值

predict(X): 预测基于 R^2值

score：评估
参考:https://blog.youkuaiyun.com/weixin_39175124/article/details/79465558

代码部分

#生成数据
import numpy as np
#生成随机数
np.random.seed(1234)
x = np.random.rand(500,3)
#构建映射关系，模拟真实的数据待预测值,映射关系为y = 4.2 + 5.7*x1 + 10.8*x2，可自行设置值进行尝试
y = x.dot(np.array([4.2,5.7,10.8]))

先尝试调用sklearn的线性回归模型训练数据

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline

# 调用模型
lr = LinearRegression(fit_intercept=True)
# 训练模型
lr.fit(x,y)
print("估计的参数值为：%s" %(lr.coef_))
# 计算R平方
print('R2:%s' %(lr.score(x,y)))
# 任意设定变量，预测目标值
x_test = np.array([2,4,5]).reshape(1,-1)
y_hat = lr.predict(x_test)
print("预测值为: %s" %(y_hat))

估计的参数值为：[ 4.2 5.7 10.8]
R2:1.0
预测值为: [85.2]

最小二乘法的矩阵求解

class LR_LS():
    def __init__(self):
        self.w = None      
    def fit(self, X, y):
        # 最小二乘法矩阵求解
        #============================= show me your code =======================
        self.w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
        #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        #============================= show me your code =======================
        y_pred = X.dot(self.w)
        #============================= show me your code =======================
        return y_pred

if __name__ == "__main__":
    lr_ls = LR_LS()
    lr_ls.fit(x,y)
    print("估计的参数值：%s" %(lr_ls.w))
    x_test = np.array([2,4,5]).reshape(1,-1)
    print("预测值为: %s" %(lr_ls.predict(x_test)))

估计的参数值：[ 4.2 5.7 10.8]
预测值为: [85.2]

梯度下降法

class LR_GD():
    def __init__(self):
        self.w = None     
    def fit(self,X,y,alpha=0.02,loss = 1e-10): # 设定步长为0.002,判断是否收敛的条件为1e-10
        y = y.reshape(-1,1) #重塑y值的维度以便矩阵运算
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros((d)) #将参数的初始值定为0
        tol = 1e5
        #============================= show me your code =======================
        while tol > loss:
            h_f = X.dot(self.w).reshape(-1,1) 
            theta = self.w + alpha*np.mean(X*(y - h_f),axis=0) #计算迭代的参数值
            tol = np.sum(np.abs(theta - self.w))
            self.w = theta
        #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lr_gd = LR_GD()
    lr_gd.fit(x,y)
    print("估计的参数值为：%s" %(lr_gd.w))
    x_test = np.array([2,4,5]).reshape(1,-1)
    print("预测值为：%s" %(lr_gd.predict(x_test)))