k-means(k均值算法) + 欧几里德距离 +PCA降维 + precision/recall/F-measure算法评估指标 + python实现 （全知识点）

最新推荐文章于 2025-05-20 11:23:18 发布
原创 最新推荐文章于 2025-05-20 11:23:18 发布 · 3.3k 阅读 · 11 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#聚类 #数据挖掘

本文深入解析K-means聚类算法，涵盖其定义、目的、原理、步骤及弊端解决方案，同时探讨了聚类算法的分类，包括分区、层次、基于图、基于模型及其他类型。文中还介绍了欧几里得距离、Manhattan距离、PCA降维等关键概念，并提供了Python代码实例。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

k-means 案例实操

先来看下Clustering Algorithms聚类算法的分类：

1.Partitioning：
Construct k partitions and iteratively update the partitions
（1）k-means(k-均值)
（2） k-medoids(k-中心点)

2.Hierarchical：（层次聚类）
Create a hierarchy of clusters (dendrogram 树状图)
（1）Agglomerative clustering (bottom-up)
（2）Conglomerative clustering (top-down)

3.Graph-based clustering：
Graph-cut algorithms (Spectral Clustering)

4.Model-based clustering
Mixture of Gaussians

5.Other types:
（1）Non-parametric Bayesian (Latent Dirichlet Allocation)
（2）Expectation Maximisation (EM) algorithm
（3）and many more …

k-means(k-均值)

定义

聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程，聚类就是一种发现这种内在结构的技术，是无监督学习

目的

给无标签的数据 (或者称为 instance) 分类

宏观来说这个算法是用来干什么的：

  1. 通过 训练数据集(train dataset) 和 k-means算法 找到每个分类的中心点(cluster centre)
  2. 在测试或应用时，计算 测试数据点 或 应用数据点(instance) 距离各个分类中心点的距离
  3. 测试数据或应用数据 距离哪个点最近，就被分到哪一类去

所以，这个算法要做的就是怎么通过训练数据集找到这些分类的中心点
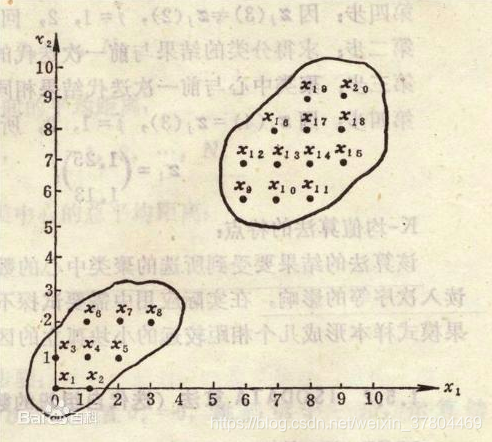
在这里插入图片描述

原理 --找聚类中心(cluster centre)

我们要做的就是最小化下面的那个公式
公式的意义： 假如所有的点都被分到了正确的类中，那么所有的点到他们所归属的类中心的距离之和是最小的
在这里插入图片描述

步骤
  • Input
    • cluster 的个数k
    • 含有N 个instances的数据集 S = {x1, …, xN}， 每个instance都是 d 维 的实数向量(xi ∈ Rd)，代表instance的d个特征(features)
  1. 从数据集中随机取 k个instances（用于初始化cluster centres，显然每个instance 代表一个cluster centre）
  2. 将其余的instances分类于与其最近的cluster（计算每个instance与k个cluster centres 的距离，将其归类于距离最小的那个cluster）
  3. 计算每个cluster里所有instances的平均值，更新cluster centre
  4. 在第2步，第3步重复，直到收敛（收敛：在做第2步，第2步时，所有点的分类都不再改变）
k-means 算法的弊端及解决方案

  1. 结果非常依赖初始化时随机选择，或者说 受初始化时选择k个点的影响特别大

  2. 可能某个分类被圈在一个很小的局部范围，并不是全局最优
    解决方案：用不同的初始化数据（k个数据），重复聚类过程多次，并选择最佳的最终聚类。那怎么评估聚类的好坏呢？例如，评估维度有：（下一个模块有详细讲解）
    – 1. smallest number of iterations before convergence
    在聚类中心值收敛前，使用了最少迭代次数
    – largest total distance between the final cluster means
    最终的的cluster means值相加，值最大，也就是说聚类中心点之间的距离越大越好

  3. 离群值对平均值的影响非常大

  4. 聚类中心(means)不是集群中的点
    解决方案：从每个分类中，分别选择其中数据作为初始化聚类中心

涉及知识点

1. 欧几里得距离（Euclidean Distance）

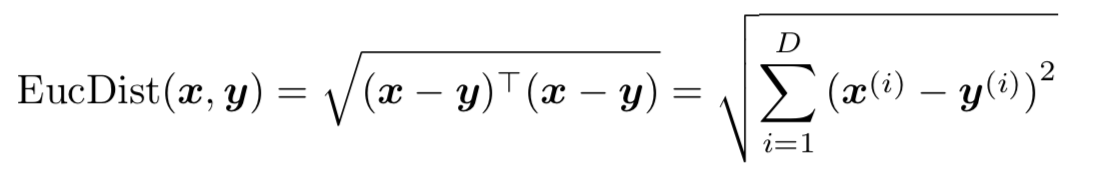
在这里插入图片描述

import numpy as np

p1 = np.array([1,2,3])
p2 = np.array([4,5,6])

sum = 0
for i in range(len(p1)):
    sum += pow(p2[i]-p1[i],2)
dis = np.sqrt(sum)

print(dis)

#5.196152422706632
2. Manhatten距离

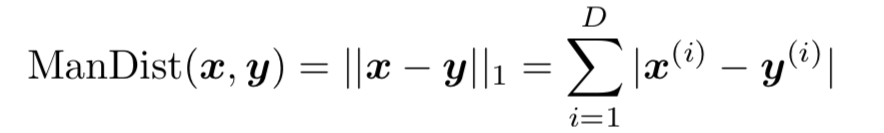
在这里插入图片描述

    def distManhatten(self, x, y):
        distance = sum(abs(x-y))
        return distance
3. 降维：PCA（Principal Component Analysis）

如果数据features太多（维度很多），需要进行降维处理，降到二维或三维，方便进行图像输出，具体理论介绍在这里

例子实现二维降到一维

import numpy as np


data = np.array([[0.9, 1.0],
                 [2.4, 2.6],
                 [1.2, 1.7],
                 [0.5, 0.7],
                 [0.3, 0.7],
                 [1.8, 1.4],
                 [0.5, 0.6],
                 [0.3, 0.6],
                 [2.5, 2.6],
                 [1.3, 1.1]])
  
# 各元素与平均值的差值 （defferences）
X = data - np.reshape(np.mean(data,axis=0),(-1,data.shape[1]))

# 协方差矩阵（coveriance  matrix ）
C = (1/data.shape[0]) * np.dot(X.transpose(),X)

# 特征值（eigenValues）与 特征向量（eigenVectors）
eigenValues, eigenVectors = np.linalg.eigh(C)
print('\neigenValues =', np.round(eigenValues, 2))
print('\neigenVectors =', eigenVectors)

# 取最大特征值对应的特征向量 叫"转换矩阵"
U = (eigenVectors[:, np.argsort(-eigenValues)[0:1]])
print('\nU =', U)

# Principal Component 主成分
PCA = np.dot(X,U).transpose()
print('\nPCA :', PCA)  


# eigenValues = [0.03 1.13]
#
# eigenVectors = [[ 0.68075138 -0.73251454]
#                 [-0.73251454 -0.68075138]]
#
# U = [[-0.73251454]
#      [-0.68075138]]
#
# PCA : [[ 0.40200434 -1.78596968 -0.29427599  0.89923557  1.04573848 -0.5295593 # 0.96731071  1.11381362 -1.85922114  0.04092339]]
k-means 聚类算法衡量指标

（聚类效果的评价方式大体上可分为性能度量和距离计算两类。）

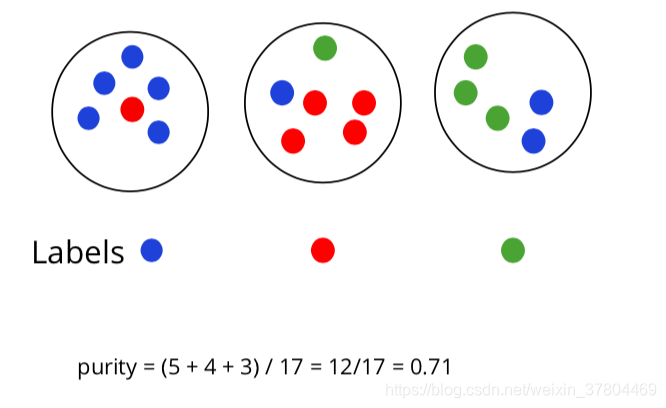
1.purity(纯度)

cluster中点最多的那个颜色，定为这个cluster的label。在这个cluster 中和label色不同的点，是错误分类。
在这里插入图片描述
栗子：
在这里插入图片描述

2.NMI ： Normalised Mutual Information (归一化互信息)
3.Rand index (RI)
  • Positive = same cluster
  • Negative = different clusters
  • TP = No. of item pairs that are in the same cluster and belong to the same class
  • FP = No. of item pairs that are in the same cluster but belong to different classes
  • TN = No. of item pairs that are in different clusters and belong to different classes
  • FN = No. of item pairs that are in different clusters but belong to the same class

总结下来可以理解为，positive是分在了同一个cluster， negative是分在了不同的cluster。Ture 和 False 指紧跟它的P 和 N 是分类正确还是错误。

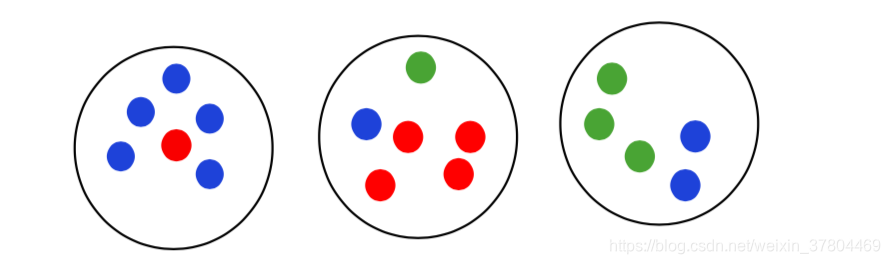
在这里插入图片描述
相同的例子：
在这里插入图片描述
TP + FP: 是不管分类是否正确，被分在了同一个cluster的item pairs
TP: 同一个class的点被正确的分在了同一个cluster中
TN + FN：是不管分类是否正确，被分在了不同的cluster的item pairs
FN：同一个class的点被正确的分在了不同的cluster中
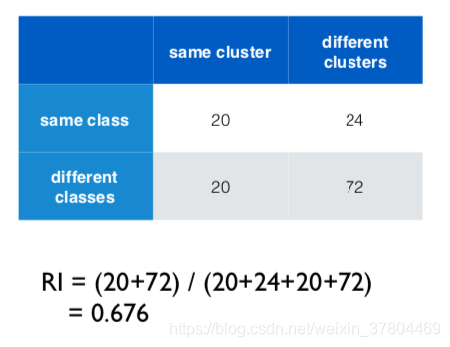
在这里插入图片描述

在这里插入图片描述

3. P (precision) / R (recall) / F (F-measure)
  • P = TP / (TP + FP)
  • R = TP / (TP + FN)
  • F = 2PR / (P + R)

用上面的例子，以及我们在 RI 中得出的的 TP、FP、TN、FN 的值，计算得出：

  • P = TP / (TP+FP) =20 / (20+20) = 0.5
  • R = TP / (TP + FN) = 20 / (20 + 24) = 0.45
  • F = 2PR / (P + R) = 0.47
案例及代码实现（python）
一文速学数模-聚类模型(一)K-means聚类算法详解+Python代码实例
master_hunter的博客
08-07 1万+
博主共参与了数十场数学建模，其中对于未给出标签的数据进行分析时一般第一个想到的就是聚类算法。聚类算法分析又称群分析，它是研究（样品或指标）分类问题的一种统计分析方法，同时也是数据挖掘的一个重要算法。聚类（Cluster）分析是由若干模式（Pattern）组成的，通常，模式是一个度量（Measurement）的向量，或者是多维空间中的一个点。聚类分析以相似性为基础，在一个聚类中的模式之间比不在同一聚类中的模式之间具有更多的相似性。......
KMeans 算法的应用与评价
weixin_42596530的博客
01-31 756
kmeans
机器学习——聚类算法KMeans及其评估方法
gjinc的博客
06-19 1947
聚类算法是一种典型的无监督学习算法，是根据样本之间的相似性，将样本分划到不同的类别中对于不同的相似度计算⽅法，会得到不同的聚类结果，常⽤的相似度计算⽅法有欧式距离法。
聚类f_measure 评价指标(python 实现)
只想买把蝴蝶knife
01-28 2534
def f_measure(cluster, labels): def get_set(data): products=[] for i in itertools.product(data, data): temp = list(i) temp.sort() products.append(tuple(temp)) products = [(i,j) for i,j in prod
深入探究KMeans-PCA降维技术在数据分析中的应用
最新发布
weixin_36483050的博客
05-20 839
手写数字识别是计算机视觉和模式识别领域的经典问题之一。它不仅在日常生活中有着广泛的应用，例如邮政编码的自动识别、银行支票的数字处理等，而且也是评估和学习机器学习算法性能的常用数据集。通过解决手写数字识别问题，我们可以更好地理解如何应用KMeans和PCA这两种算法来处理实际问题，并且可以探索它们在图像识别领域中的潜在优势。在本案例中，我们将使用著名的MNIST数据集。MNIST包含了成千上万的手写数字图片，每张图片都是28x28像素的灰度图。
python准确率 召回率计算_推荐系统评测指标—准确率(Precision)、召回率(Recall)、F值(F-Measure)...
weixin_39622643的博客
12-06 1860
准确率和召回率是广泛用于信息检索和统计学分类领域的两个度量值，用来评价结果的质量。其中精度是检索出相关文档数与检索出的文档总数的比率，衡量的是检索系统的查准率；召回率是指检索出的相关文档数和文档库中所有的相关文档数的比率，衡量的是检索系统的查全率。一般来说，Precision就是检索出来的条目(比如：文档、网页等)有多少是准确的，Recall就是所有准确的条目有多少被检索出来了。正确率、召回率和 ...
数学之路(3)-机器学习(3)-机器学习算法-欧氏距离(1)
jishublog
08-31 448
机器学习算法 之欧氏距离 欧氏距离通常用于衡量2个点之间的距离，注意这2个点可以是定义在2维空间的，也可以是定义在3维空间或者n维空间的。 二维的公式 　ρ = sqrt( (x1-x2)^2+(y1-y2)^2 ) 三维的公式　　ρ = sqrt( (x1-x2)^2+(y1-y2)^2+(z1-z2)^2 ) n维空间的公式　　n维欧氏空间是一个点集,它的每个点 X 可以表...
k-means聚类算法详解
magicmens的博客
04-06 1万+
K-means 是我们最常用的基于欧式距离的聚类算法，其认为两个目标的距离越近，相似度越大。
klkmeans:KL散度的K-Means实现（而不是平方欧几里德距离）
05-23
"klkmeans" 是一个特定的实现，它使用了“KL散度”作为聚类算法K-Means中的距离度量，而不是传统的平方欧几里德距离。这表明它是一个针对K-Means算法的变种，旨在提供一种不同的数据聚类方式。 **描述分析：** ...
Bisectingk-means聚类算法实现
02-26
Bisectingk-means聚类算法，即二分k均值算法，它是k-means聚类算法的一个变体，主要是为了改进k-means算法随机选择初始质心的随机性造成聚类结果不确定性的问题，而Bisectingk-means算法受随机选择初始质心的影响...
KL散度K-Means实现：超越传统平方欧几里德距离
实现K-Means算法时，Python提供了许多库，比如NumPy和SciPy用于数值计算，而像scikit-learn这样的库已经内置了K-Means算法的实现，如果要使用KL散度作为距离度量，则可能需要自定义算法部分逻辑。 6. 压缩包子文件...
机器学习（17）无监督学习 -- K-means算法与性能评估
great_yzl的博客
09-13 3428
目录 一、K-means 1、概念 2、过程 3、API（K-means） 二、K-means性能评估 1、轮廓系数 2、API（轮廓系数） 一、K-means 1、概念 无监督学习：没有目标值（没有标签）。 （聚类一般在分类之前，没有目标值的时候使用聚类） 采用迭代式的算法，直观易懂且实用。 缺点：容易受到局部最优解（避免：多次聚类，取多次聚类中心）。 最优解：k个中心点挤在一起。 例：对这些人物的分类，没有目标值，就是无监督学习。 2、过程 例...
PCA 和欧氏距离方法设计的人脸识别matlab程序
01-07
pca方法提取的特征值，用欧式距离进行的分类器设计，进行人脸识别。
K-means算法代码实现（python）
热门推荐
江南小帅瓜的博客
07-04 1万+
K-means算法代码实现以及解决质心选择问题 计算距离 距离通常使用欧几里得距离来衡量 def euclDistance(vector1, vector2): return np.sqrt(sum((vector2 - vector1) ** 2)) 初始化质心 def initCentroids(data, k): numSamples, dim = data.shape ...
k-means算法（欧式距离）
菜鸟一个
03-29 1万+
无聊时写个k-means 采用欧式距离，进行分类，随机n个三维（a,b,c）点，聚类成k类 import java.util.*; public class KMeans { public static void main(String[] args){ //K-Means ，首先随机生成n个点 int n = 20; int k = ...
roc曲线python实现_ROC曲线、AUC、Precision、Recall、F-measure理解及Python实现
weixin_39874881的博客
11-29 464
本文首先从整体上介绍ROC曲线、AUC、Precision、Recall以及F-measure，然后介绍上述这些评价指标的有趣特性，最后给出ROC曲线的一个Python实现示例。一、ROC曲线、AUC、Precision、Recall以及F-measure二分类问题的预测结果可能正确，也可能不正确。结果正确存在两种可能：原本对的预测为对，原本错的预测为错；结果错误也存在两种可能：原本对的预测为错，...
auc曲线 python,ROC曲线、AUC、Precision、Recall、F-measure理解及Python实现
weixin_29146599的博客
03-18 598
本文首先从整体上介绍ROC曲线、AUC、Precision、Recall以及F-measure，然后介绍上述这些评价指标的有趣特性，最后给出ROC曲线的一个Python实现示例。一、ROC曲线、AUC、Precision、Recall以及F-measure二分类问题的预测结果可能正确，也可能不正确。结果正确存在两种可能：原本对的预测为对，原本错的预测为错；结果错误也存在两种可能：原本对的预测为错，...
k-means聚类算法 python实现_K-means聚类算法及python代码实现
weixin_42500866的博客
01-27 1728
K-means聚类算法(事先数据并没有类别之分！所有的数据都是一样的)1、概述K-means算法是集简单和经典于一身的基于距离的聚类算法采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为类簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。2、核心思想通过迭代寻找k个类簇的一种划分方案，使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。k个...
动态聚类算法之聚类分析基础和实现基于欧式距离的 K-means 聚类法matlab实现
一只在cv道路上爬行的小乌龟~
11-18 4189
1.聚类分析基础 function [ distance ] = step1_mission( v1, v2 ) %%%%%%%%%% Begin %%%%%%%%%% [m,p]=size(v1); [n,p]=size(v2); distance=zeros(m,n); for mm=1:m for nn=1:n distance(mm,nn)=sqrt(sum((v1(mm,:)-v2(nn,:)).^2));
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Enzo 想砸电脑

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值