DS证据理论

最新推荐文章于 2025-06-12 15:28:02 发布

原创最新推荐文章于 2025-06-12 15:28:02 发布 · 7k 阅读

17 ·

CC 4.0 BY-SA版权

1、基本概念

假设空间（识别框架）：对于全域X，X={A,B}，那么假设空间为{空，A，B，AB}
Mass函数和BPA：mass函数给假设空间每一个假设都分配了概率，我们称为基本概率分配（BPA, Basic Probability Assignment），如下式
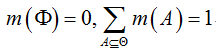
在这里插入图片描述
由上式可以看出，基本概率分配在空集是为0，假设空间内其他假设概率和为1。比如一个证人证明一个案件的犯罪嫌疑人，证人给出所有可能性的概率和是1，其中空的概率是0，代表证人不是一无所知的，一无所知的也不会作为证人。
信度函数(Belief function): 对于假设A ，它的信度函数为所有真属于 A 的假设，即 B ，的mass值的和
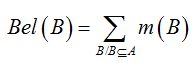
在这里插入图片描述
似然函数 (Plausibility function): 对于假设A ，它的似然函数为所有与 A 相交不为空的假设 B 的mass值的和

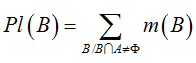
信任区间:由信任函数与似然函数组成的闭区间[Bel(A),Pl(A)]则为假设 A 的信任区间，表示对假设 A 的确认程度
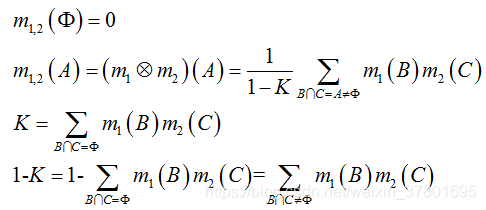
在这里插入图片描述
上述指标为一个主体对于事件的确认程度，将多个主体的结果进行合并，得到事件的确认度。
合成规则为两个mass函数 m1 和 m2, 对于假设A的合成结果等于两个主体的假设中，所有相交为 A 的假设的mass函数值的乘积的和，再除以一个归一化系数 1-K。归一化系数 1-K 中的 K 的含义是证据之间的冲突。