模型训练与测试---梯度下降与牛顿法与优化器与反向传播 ·1.

昨天是：大疆的笔试题，多次问了优化器的问题。本文仅作为个人学习笔记，不作为分享

https://blog.youkuaiyun.com/google19890102/article/details/69942970
目前找到比较好的文章

https://zhuanlan.zhihu.com/p/22252270
https://zhuanlan.zhihu.com/p/32230623
其次觉得还OK的文章

逻辑：

理清优化器，应该先理清楚，我们是如何梯度下降的，因为优化器的作用是辅助更新和计算影响模型训练和模型输出的网络参数，从而最小化或最大化损失函数。关于这部分我们需要理清的是为什么？为什么是梯度下降，以及在大规模的网络中，我们如何结合梯度下降和链式法则来更新参数，从而让模型更好。深度学习的部分都是围绕这个进行的，包括激活函数的选择，优化器的选择的，为什么用BN层，目前深度学习的三大法宝都是通过这三方面来进行的。而至于落地方面的话就需要了解到如何进行链式法则求导。 所以我们的逻辑会先讲清楚，为什么？然后我们在手算一次简单的怎么做。

https://zhuanlan.zhihu.com/p/39842768

就是说无论我的输入是什么，我都拟合好了一个方程，让得到的y是最小的。无论我的数据输入的是啥，我这个方程对应的y都是最小的，也就是对应的着其他的参数来说这个是最小的。比如分类的话就是无论我输入都是什么猫，那么最终sigmoid的输出都是猫的概率要大于0.5，来判断这是猫，实际上我们做的就是在求一个方程。最终这个方程该激活的都被激活了。

而上面提到的一个关键问题就是优化问题，我们希望训练一个模型出来，无论我输入什么的数据，他的损失函数都是最小的。这就是我们深度学习或者说优化模型的关键。为啥有训练集合，就是反复放到模型直到这些训练集合的loss最小，我们就觉得不错哦，但是同时也要注意过拟合的存在。无论是训练和测试，训练是找到一组参数让损失函数无论在什么数据的输入都是最小的。如果从曲面来看就是如下图：下图有很多中组合的参数，但是真正能够让损失函数最小的却只有一个地方，这就是我们的优化问题的关键了。

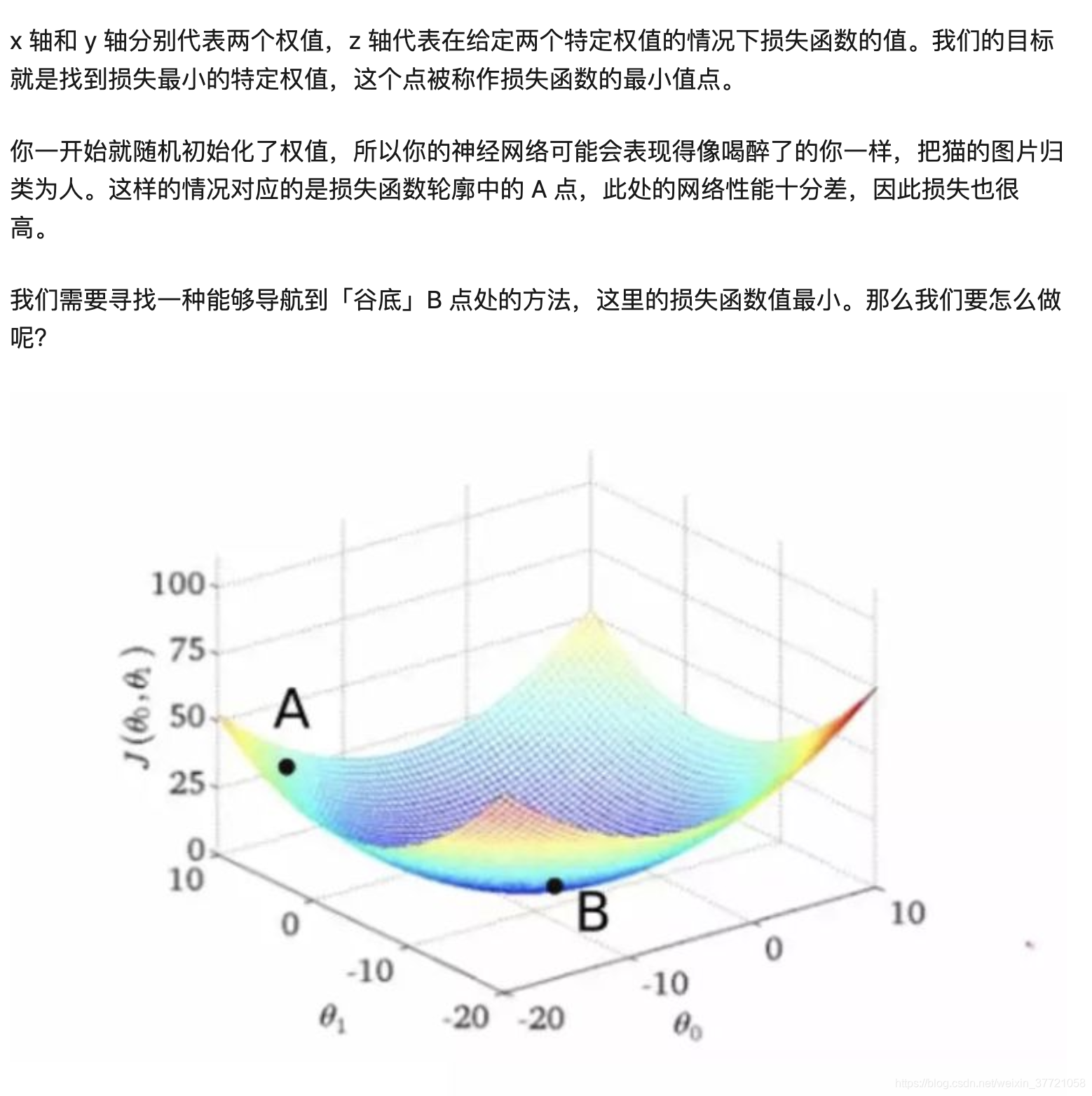
而如何找到这个最小的位置，就是我们第二部分会提到了的牛顿法和梯度下降的原理。而上面的无论是激活函数的选择，还是我们的优化器的选择，还是BN层都会涉及到梯度下降，所以弄清楚梯度下降，深度学习基本上就结束了。

为什么可以，牛顿法与梯度下降

梯度下降法是基于搜索的一种优化方法

先说泰勒展开式：机器学习里面我们用到了泰勒展开是GBDT和XGBOOST，前者用的是一阶的泰勒展开，后者用的是二阶的泰勒展开。无论是一阶展开还是二阶展开，都是近似，阶数越高，那么就越准确，牛顿法对应的是二阶泰勒展开，梯度下降对应的是一阶泰勒展开，所以实际上牛顿法会比梯度下降更好，但是牛顿法涉及到二阶泰勒展开，计算更加复杂，所以从目前来看我们会用一阶泰勒展开的梯度下降。

泰勒展