堆排序

堆和完全二叉树的关系：

1. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

2. 堆：堆又分为大根堆和小根堆。

3. 堆和二叉树的有什么关系：我们假设有一颗二叉树处理满足作为完全二叉树的基础上，对于任意一个拥有父节点的   子节点，其数值均不小于父节点的值，这样层层地推，就是根结点的值最下，这样的数称为小根堆。我们假设有一颗二叉树处理满足作为完全二叉树的基础上，对于任意一个拥有 父节点的子节点，其数值均不大于父节点的值，这样层层地推，就是根结点的值最下，这  样的数称为大根堆 

 

父节点左孩子的下标：2*i+1

父节点又孩子的下标：2*i+2

子节点的父节点的下标：（i-1）/2

---

 

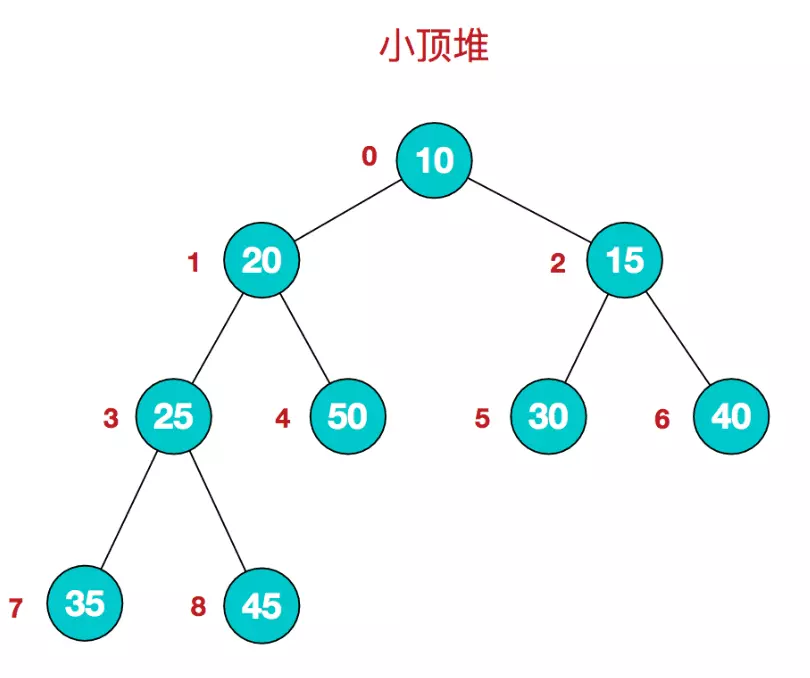
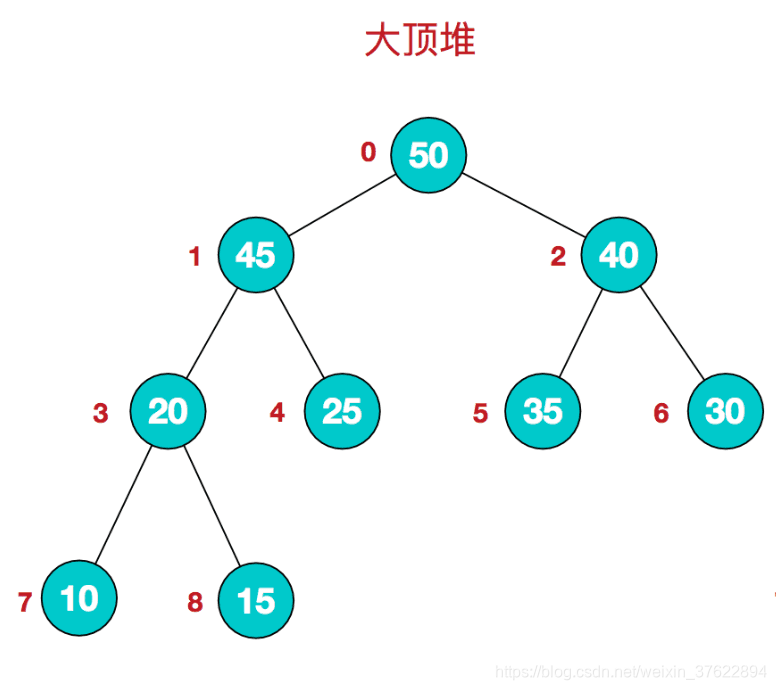                          （图转载）

---

明确大根堆和小根堆后，我们继续说堆排序：

堆排序：堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树 时间复杂度：Ο(nlogn)

动画演示：

 

 代码的实现：

#include<iostream>
#include<vector>
using namespace std;

void _print(vector<int>arr);

void swap06(vector<int>&arr, int i, int j)
{
	int temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}

void maxheapInsrt(vector<int>&arr, int index)
{
	while (arr[index] > arr[(index - 1) / 2])  //当index=0时，-1/2=0；自己就结束了，不怕进入负数，无线循环
	{
		swap06(arr, index, (index - 1) / 2);
		index = (index - 1) / 2;
	}

}

void heapify(vector<int>&arr, int index,int size)
{
	int left = 2*index + 1;
	while (left < size)
	{
		int large = left + 1 < size&&arr[left + 1] > arr[left] ? left+1 : left;
		large = arr[large] > arr[index] ? large : index;
		if (large == index)
			break;
		swap06(arr, large, index);
		index = large;
		left = index * 2 + 1;
	}

}

vector<int> HeapSort(vector<int>& arr)
{
	//cout << arr.size() << endl;
	if (arr.size() == 0 || arr.size() == 1)
		return arr;
	for (int i = 0; i < arr.size(); i++)
	{
		maxheapInsrt(arr, i);  //生成最大堆
	}
	
	int size = arr.size();
	swap06(arr, 0, --size);//把堆的最后一个元素和堆头的元素交换，并把堆的大小减一，这样堆最后一个元素就是整个堆的最大值
	while (size > 0)
	{
		heapify(arr, 0, size);  //heapify的函数的作用就是把交换后的堆，再变为一个最大堆的形式
		swap06(arr, 0,--size);

	}
	
	return arr;

}

void _print(vector<int>arr)
{
	for (int i = 0; i < arr.size(); i++)
	{
		cout << arr[i] << ' ';
	}
	cout << endl;
}

int main()
{
	vector<int>arr ={ 0, 1, 7, 6, 5, 7, 9 };
	vector<int> arr1;
	_print(arr);
	arr1=HeapSort(arr);
	_print(arr1);

	system("pause");
	return 0;
}

 

参考文献

https://blog.youkuaiyun.com/u013384984/article/details/79496052

https://www.cnblogs.com/wanglei5205/p/8733524.html