快速幂取模（O（logn)算法

所谓的快速幂，实际上是快速幂取模的缩写，简单的说，就是快速的求一个幂式的模(余)。在程序设计过程中，经常要去求一些大数对于某个数的余数，为了得到更快、计算范围更大的算法，产生了快速幂取模算法。[有读者反映在讲快速幂部分时有点含糊，所以在这里对本文进行了修改，作了更详细的补充，争取让更多的读者一目了然]

a^b mod c = (a mod c)^b mod c

a^b mod c = (a²)^b/2 mod c , b为偶数 

a^b mod c = ((a²)^b/2·a) mod c , b为奇数

我们先从简单的例子入手：求= 几。

算法1.首先直接地来设计这个算法：

[cpp]  view plain  copy

1. int ans = 1;  
2. for(int i = 1;i<=b;i++)  
3. {  
4. ans = ans * a;  
5. }  
6. ans = ans % c;  

这个算法的时间复杂度体现在for循环中，为O（b）.这个算法存在着明显的问题，如果a和b过大，很容易就会溢出。

那么，我们先来看看第一个改进方案：在讲这个方案之前，要先有这样一个公式：

.这个公式大家在离散数学或者数论当中应该学过，不过这里为了方便大家的阅读，还是给出证明：

引理1：

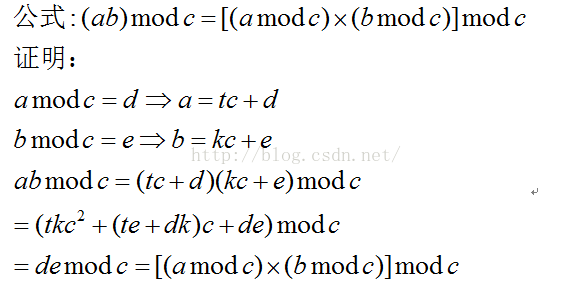
上面公式为下面公式的引理，即积的取余等于取余的积的取余。

证明了以上的公式以后，我们可以先让a关于c取余，这样可以大大减少a的大小，

于是不用思考的进行了改进：

算法2：

[cpp]  view plain  copy

1. int ans = 1;  
2. a = a % c; //加上这一句  
3. for(int i = 1;i<=b;i++)  
4. {  
5. ans = ans * a;  
6. }  
7. ans = ans % c;  

聪明的读者应该可以想到，既然某个因子取余之后相乘再取余保持余数不变，那么新算得的ans也可以进行取余，所以得到比较良好的改进版本。

算法3：

[cpp]  view plain  copy

1. int ans = 1;  
2. a = a % c; //加上这一句  
3. for(int i = 1;i<=b;i++)  
4. {  
5. ans = (ans * a)% c;//这里再取了一次余  
6.    
7. }  
8. ans = ans % c;  

这个算法在时间复杂度上没有改进，仍为O(b)，不过已经好很多的，但是在c过大的条件下，还是很有可能超时，所以，我们推出以下的快速幂算法。

快速幂算法依赖于以下明显的公式，我就不证明了。

有了上述两个公式后，我们可以得出以下的结论：

1.如果b是偶数，我们可以记k = a²mod c，那么求(k)^b/2 mod c就可以了。

2.如果b是奇数，我们也可以记k =a² mod c，那么求

((k)^b/2 mod c × a ) mod c =((k)^b/2 mod c * a) mod c 就可以了。

 

那么我们可以得到以下算法：

算法4：

[cpp]  view plain  copy

1. int ans = 1;  
2. a = a % c;  
3. if(b%2==1)  
4. ans = (ans *a) mod c; //如果是奇数，要多求一步，可以提前算到ans中  
5. k = (a*a) % c; //我们取a2而不是a  
6. for(int i = 1;i<=b/2;i++)  
7. {  
8. ans = (ans *k) % c;  
9. }  
10. ans = ans % c;  

 

我们可以看到，我们把时间复杂度变成了O(b/2).当然，这样子治标不治本。但我们可以看到，当我们令k = (a * a)mod c时，状态已经发生了变化，我们所要求的最终结果即为(k)^b/2 mod c而不是原来的a^b mod c，所以我们发现这个过程是可以迭代下去的。当然，对于奇数的情形会多出一项a mod c，所以为了完成迭代，当b是奇数时，我们通过

ans = (ans * a) % c;来弥补多出来的这一项，此时剩余的部分就可以进行迭代了。

 

形如上式的迭代下去后，当b=0时，所有的因子都已经相乘，算法结束。于是便可以在O（log b）的时间内完成了。于是，有了最终的算法：快速幂算法。

算法5：快速幂算法

 

[cpp]  view plain  copy

1. int ans = 1;  
2. a = a % c;  
3. while(b>0)  
4. {  
5.    
6. if(b % 2 == 1)  
7. ans = (ans * a) % c;  
8. b = b/2;  
9. a = (a * a) % c;  
10. }  

将上述的代码结构化，也就是写成函数：

[cpp]  view plain  copy

1. int PowerMod(int a, int b, int c)  
2. {  
3. int ans = 1;  
4. a = a % c;  
5. while(b>0)  
6. {  
7.    
8. if(b % 2 = = 1)  
9. ans = (ans * a) % c;  
10. b = b/2;  
11. a = (a * a) % c;  
12. }  
13. return ans;  
14. }  

本算法的时间复杂度为O（logb），能在几乎所有的程序设计（竞赛）过程中通过，是目前最常用的算法之一。

By  夜せ︱深