对付回文序列的利器——马拉车算法

马拉车算法（Manacher，我觉得应该读马拿车啊。。。）是基于中心扩散算法的一种改进。

什么叫中心扩散算法呢?

举个简单的例子，假设有字符串1234135314，我们从5开始往两边扩散，就能够，经过O(n）时间（实际上远远达不到）就可以找到这个字符串的子串 ：13531。

可能细心的人已经发现这个算法的小漏洞——如果回文串是偶数长度的呢？

比如：1344554451的正确答案应当是445544。但是无法利用中心扩散的循环while s[i-k]==s[i+k]:k++这个核心代码来搜索中心扩散的序列。

其实，做法也很简单啦。既然它要奇数的序列才可以，那我就构造一个呗。

比如

'#'+'#'.join(list(s))+'#'

这段python代码写的很简略，就是假如s是'1234'，那么就变成‘#1#2#3#4#’，你可能会问了：真的长度是多少都能变成奇数长度吗？实际上很容易证明啊，这个相当于new_len=2*len+1 并且2k+1显然是奇数嘛！

好了这样的话就可以在‘#’字符处搜索到最大范围，然后利用replaceAll方法就可以去掉所有的#，这样时间是O(n^2),

代码过于简单，就不写了。

有人说这有什么难的，而且也并不快啊，还有一种动态规划的方法呢！（自行搜索）

但是想想，动态规划利用二维数组记录，是平方空间，这个方法是2*n+1的空间呢，所以还是被优化了呢。

这个题实际上来自于leetcode第5题，一道非常古老的查找最长连续回文序列的题目。

当我提交时（用的是dp）发现竟然速度远远慢于很多人，我猜测应该还有比动态规划更加优秀的算法。

毕竟算法嘛，效率优先。

接下来隆重介绍马拉车算法。

核心的一行代码是：

        if mx>i:
            p[i]=min(p[2*index-i],mx-i)
        else:
            p[i]=1

我们先不急，用图来说话。

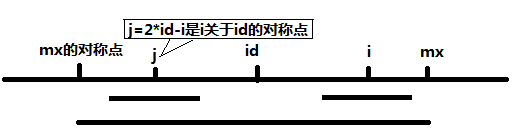
mx是以id为中心点，所能扩散到达的最远地方（就是刚才说的中心扩散法）。

那么假如i小于这个mx，我们说范围数组p[i]（从i开始能扩散到的最大半径）能够取得的值一定在两个值之间取得。

a）p[j]，其中j=2*id-i，显然就是关于id的对称点。在对称点能取得的最大扩散半径一定对i也适用。这是在p[j]扩散的范围没有超过以p[id]为中心的范围时，是适用的。

b）mx-i，这是一种权宜之计，我们并不知道是不是真的就是mx-i，但是后面还含“扩散”的代码，所以实际上先把p【i】设置可一个初值。

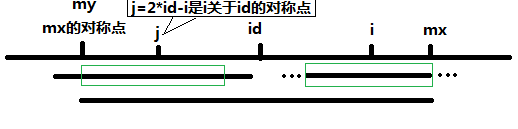
我们从上图可以看到，如果p[j]是大于mx-i的，那么只能先设置p[i]=mx-i，因为无法确定是否还要扩散。

完整的代码如下：

def Manacher(s):
    t='@#'+'#'.join(list(s))+"#$"
    p=[0 for _ in t]
    mx=0
    index=0
    max_r,max_i=0,0
    for i in range(1,len(t)-2):
        if mx>i:
            p[i]=min(p[2*index-i],mx-i)
        else:
            p[i]=1
        while i+p[i]<len(t) and i-p[i]>=0 and t[i+p[i]]==t[i-p[i]]:
            p[i]+=1
        if mx<i+p[i]:
            index=i
            mx=i+p[i]
        if max_r<p[i]:
            max_r=p[i]
            max_i=i
    r=max_r-1
    return t[max_i-r:max_i+r+1].replace('#','')

为了阻止越界，设置了开头结尾字符。可以看到刚才的判断语句后面含有扩散动作：

        while i+p[i]<len(t) and i-p[i]>=0 and t[i+p[i]]==t[i-p[i]]:
            p[i]+=1

而且当mx<=i时候，只能用最原始的方法开始扩散了id~mx之间的p值已经无法帮助我们了。

从代码来看，这一条if else语句直接优化了中心扩散的搜索过程，对于类似：

......12321412321....中mx就是最后的1，id就是中间的4，而当我们搜索到最后一个3的时候我们就可以不用从这个3开始搜索，

因为它被置为3（这里mx-i和p[j]相等），这时候再搜索就是从最后一个1之后的位置开始搜索了。

假如省略号第一个是4，那么还可以加一，否则直接就确认了这个p值。

因此所有的位置几乎只被搜索了一次，所以是O(N)的时间，这样就是大大加快平方算法的速度。