博客围绕softmax展开，它是多分类器，可计算预测对象属各类别的概率。介绍了softmax公式，说明了公式中各参数含义，还阐述了梯度计算方法，已知y的梯度，通过计算图得出z的梯度计算方式，并分情况给出具体计算结果。
softmax是一个多分类器，可以计算预测对象属于各个类别的概率。
公式
yi=S(z)i=ezi∑j=1Cezj，i=1,...,Cy_i=S(\boldsymbol{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{C}e^{z_j}}，i=1,...,Cyi=S(z)i=∑j=1Cezjezi，i=1,...,C
- z\boldsymbol{z}z是上一层的输出，
softmax的输入， 维度为CCC - yiy_iyi为预测对象属于第ccc类的概率
梯度
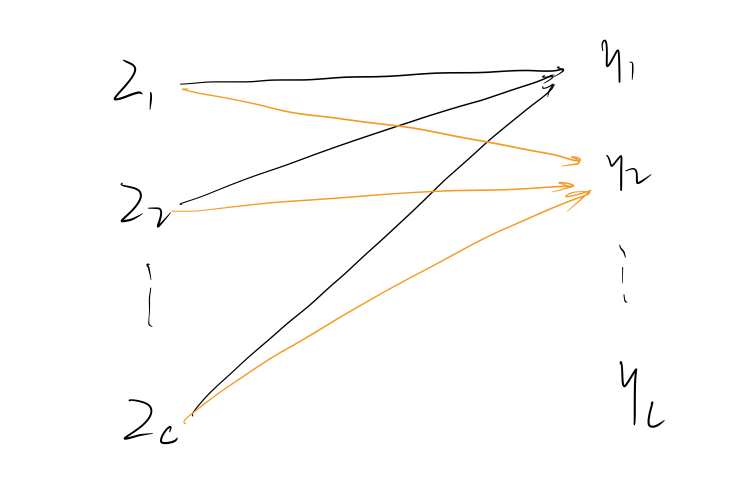
变量间的计算图如上，已知y\boldsymbol{y}y的梯度∂l∂yi,i=1,...,C\frac{\partial l}{\partial y_i}, i=1,...,C∂yi∂l,i=1,...,C，要计算z\boldsymbol{z}z的梯度∂l∂zj,j=1,...,C\frac{\partial l}{\partial z_j}, j=1,...,C∂zj∂l,j=1,...,C
从计算图中可以看到，z\boldsymbol{z}z的分量zjz_jzj对y\boldsymbol{y}y的每一个分量都有贡献，因此：
∂l∂zj=∑i=1C∂l∂yi∂yi∂zj\frac{\partial l}{\partial z_j} = \sum_{i=1}^{C}\frac{\partial l}{\partial y_i} \frac{\partial y_i}{\partial z_j}∂zj∂l=i=1∑C∂yi∂l∂zj∂yi
由于∂l∂yi\frac{\partial l}{\partial y_i}∂yi∂l已知，因此计算∂yi∂zj\frac{\partial y_i}{\partial z_j}∂zj∂yi即可！
为方便记∑j=1Cezj\sum_{j=1}^{C}e^{z_j}∑j=1Cezj为∑C\sum_C∑C
（1）i=ji=ji=j时：
∂yi∂zj=ezi∑C−eziezi∑C2=ezi∑C−ezi∑C2=yi−yi2=yi(1−yi)
\begin{aligned}
\frac{\partial y_i}{\partial z_j} & = \frac{e^{z_i}\sum_C-e^{z_i}e^{z_i}}{{\sum_C}^2} \\
&=\frac{e^{z_i}}{\sum_C} - \frac{e_{z_i}}{\sum_C}^2 \\
& = y_i-y_i^2 \\
& = y_i(1-y_i)
\end{aligned}
∂zj∂yi=∑C2ezi∑C−eziezi=∑Cezi−∑Cezi2=yi−yi2=yi(1−yi)
（2）i≠ji \neq ji̸=j
∂yi∂zj=0∑C−eziezj∑C2=−ezi∑Cezj∑C=−yiyj
\begin{aligned}
\frac{\partial y_i}{\partial z_j}
&= \frac{0\sum_C - e^{z_i}e^{z_j}}{{\sum_C}^2} \\
&= -\frac{e_{z_i}}{\sum_C}\frac{e_{z_j}}{\sum_C} \\
&=-y_iy_j
\end{aligned}
∂zj∂yi=∑C20∑C−eziezj=−∑Cezi∑Cezj=−yiyj
扫一扫
1031
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
