python标准正态分布概率_python绘制正态分布及三大抽样分布的概率密度图像-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_36431018/article/details/113538316

本文介绍了使用Python的scipy和stats库绘制正态分布、卡方分布、t分布和F分布的概率密度函数图像，包括各自函数的使用方法，并展示了这些分布的对比。通过实例展示如何利用这些库进行统计分布的可视化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文来自读者投稿，作者：黄同学

1、scipy库中各分布对应的方法

from scipy import stats
# 正态分布
stats.norm
# 卡方分布
stats.chi2
# t分布
stats.t
# F分布
stats.f

2、stats库中各分布的常用方法及其功能

对于正态分布：

stats.norm.cdf(α,均值,方差)；
stats.norm.pdf(α,均值,方差)；
stats.norm.isf(α,均值,方差)；

对于t分布：

stats.t.cdf(α,自由度)；
stats.t.pdf(α,自由度)；
stats.t.isf(α,自由度)；

对于F分布：

stats.f.cdf(α,自由度1,自由度2)；
stats.f.pdf(α,自由度1,自由度2)；
stats.f.isf(α,自由度1,自由度2)；一个简单的案例说明：

# 对于正态分布
stats.norm.cdf(0.5,2,3)
stats.norm.pdf(0.5,2,3)
stats.norm.isf(0.05,2,3)
# 对于t分布
stats.t.cdf(0.5,10)
stats.t.pdf(0.5,10)
stats.t.isf(0.0005,45)

结果如下：

3、正态分布的概率密度函数及其图象

1)正态分布的概率密度函数及其图象

2)python绘制正态分布的概率密度函数图象

x = np.linspace(-5,5,100000)
y = stats.norm.pdf(x,0,1)
plt.plot(x,y,c="red")
plt.title('正态分布的概率密度函数')

plt.tight_layout()
plt.savefig("正态分布的概率密度函数",dpi=300)

结果如下：

4、卡方分布的概率密度函数及其图象

1)卡方分布的概率密度函数及其图象

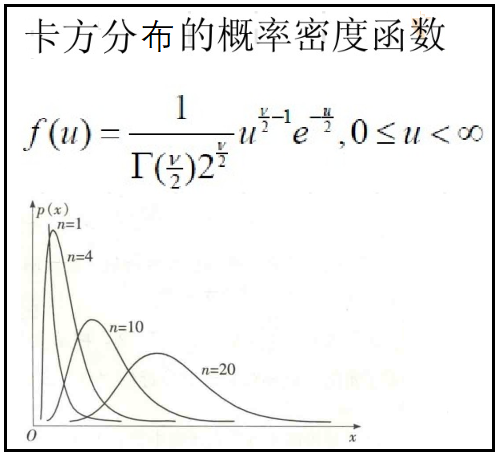
2)python绘制卡方分布的概率密度函数图象

x = np.linspace(0,100,100000)
color = ["blue","green","darkgrey","darkblue","orange"]
for i in range(10,51,10):
    y=stats.chi2.pdf(x,df=i)
    plt.plot(x,y,c=color[int((i-10)/10)])
plt.title('卡方分布')

plt.tight_layout()
plt.savefig(" 布的概率密度函数",dpi=300)

结果如下：

总结：从图中可以看出，随着自由度的增加，卡方分布的概率密度曲线趋于对称。当自由度n -> +∞的时候，卡方分布的极限分布就是正态分布。

5、t分布的概率密度函数及其图象

1)t分布的概率密度函数及其图象

2)python绘制t分布的概率密度函数图象

x = np.linspace(-5,5,100000)
y = stats.t.pdf(x_t,2)
plt.plot(x,y,c="orange")
plt.title('t分布的概率密度函数')

plt.tight_layout()
plt.savefig("t分布的概率密度函数",dpi=300)

结果如下：

3)python绘制t分布和正态分布的概率密度函数对比图

x_norm = np.linspace(-5,5,100000)
y_norm = stats.norm.pdf(x_norm,0,1)
plt.plot(x_norm,y_norm,c="black")

color = ["green","darkblue","orange"]

x_t = np.linspace(-5,5,100000)
for i in range(1,4,1):
    y_t = stats.t.pdf(x_t,i)
    plt.plot(x_t,y_t,c=color[int(i-1)])

plt.title('t分布和正态分布的概率密度函数对比图')

plt.tight_layout()
plt.savefig("t分布和正态分布的概率密度函数对比图",dpi=300)

结果如下：

总结：从图中可以看出，t分布的概率密度函数和正态分布的概率密度函数都是偶函数(左右对称的)。t分布随着自由度的增加，就越来越接近正态分布，即t分布的极限分布也是正态分布。

6、F分布的概率密度函数及其图象

1)F分布的概率密度函数及其图象

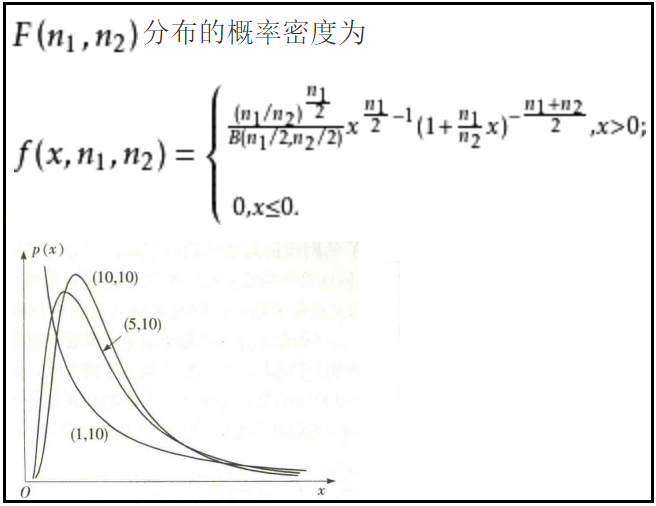
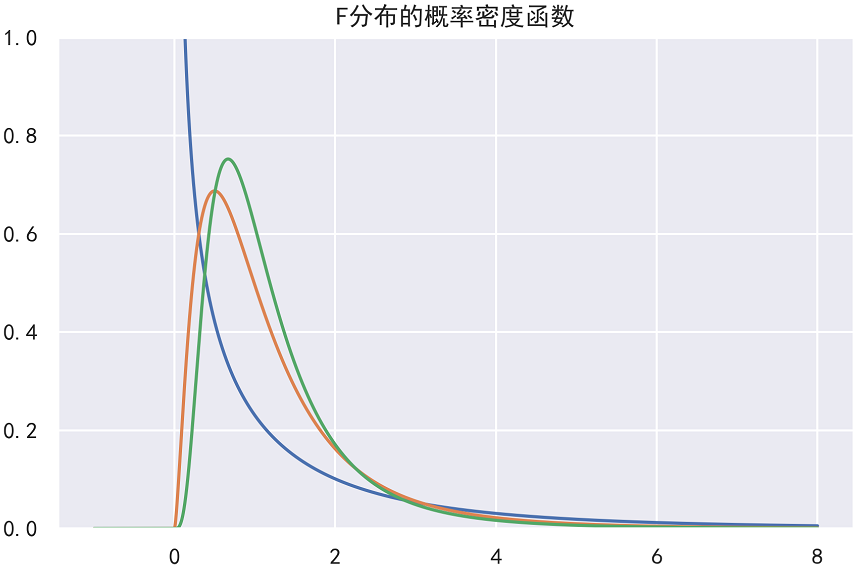
2)python绘制F分布的概率密度函数图象

x = np.linspace(-1,8,100000)
y1 = stats.f.pdf(x,1,10)
y2 = stats.f.pdf(x,5,10)
y3 = stats.f.pdf(x,10,10)
plt.plot(x,y1)
plt.plot(x,y2)
plt.plot(x,y3)
plt.ylim(0,1)
plt.title('F分布的概率密度函数')

plt.tight_layout()
plt.savefig("F分布的概率密度函数",dpi=300)

结果如下：