a上标3下标6算法_漫画：Dijkstra 算法的优化

在上一篇漫画中，小灰介绍了单源最短路径算法 Dijkstra，没看过的小伙伴可以看下：

漫画：图的 “最短路径” 问题

漫画中我们遗留了一个问题：

如何求得最短路径的详细节点，而不仅仅是距离？

在本篇中，我们将会给与解答。

我们仍然以下面这个带权图为例，找出从顶点A到顶点G的最短距离。

详细过程如下：

第1步，创建距离表和前置顶点表。

距离表的Key是顶点名称，Value是从起点A到对应顶点的已知最短距离，默认为无穷大；前置顶点表的Key是顶点名称，Value是从起点A到对应顶点的已知最短路径的前置定点。

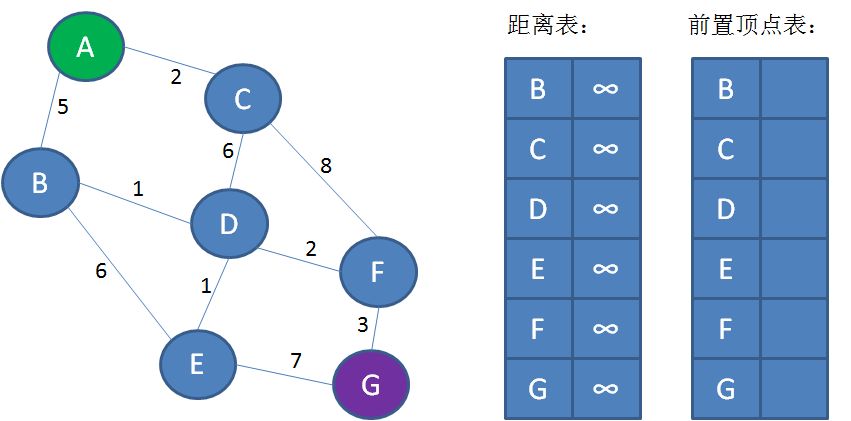
第2步，遍历起点A，找到起点A的邻接顶点B和C。从A到B的距离是5，从A到C的距离是2。把这一信息刷新到距离表当中。

同时，顶点B、C的前置顶点都是A，顶点A在邻接表中下标是0，所以把前置顶点表的B、C值更新为0：

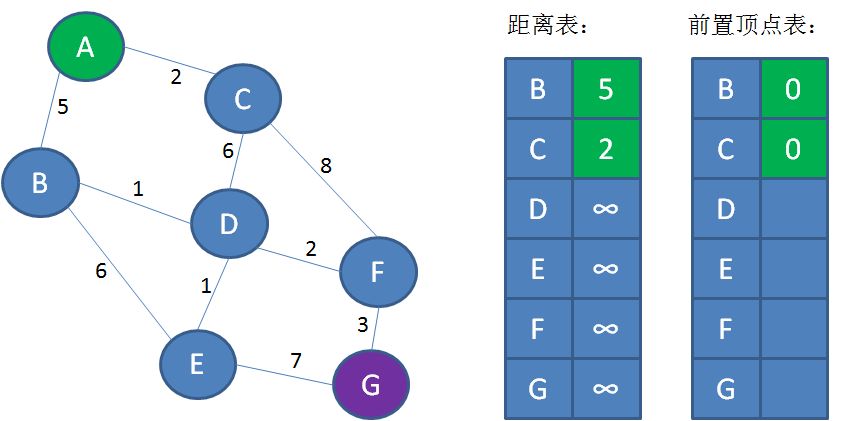
第3步，从距离表中找到从A出发距离最短的点，也就是顶点C。

第4步，遍历顶点C，找到顶点C的邻接顶点D和F(A已经遍历过，不需要考虑)。从C到D的距离是6，所以A到D的距离是2+6=8；从C到F的距离是8，所以从A到F的距离是2+8=10。把这一信息刷新到表中。

同时，顶点D、F的前置顶点都是C，顶点C在邻接表中下标是2，所以把前置顶点表的D、F值更新为2：

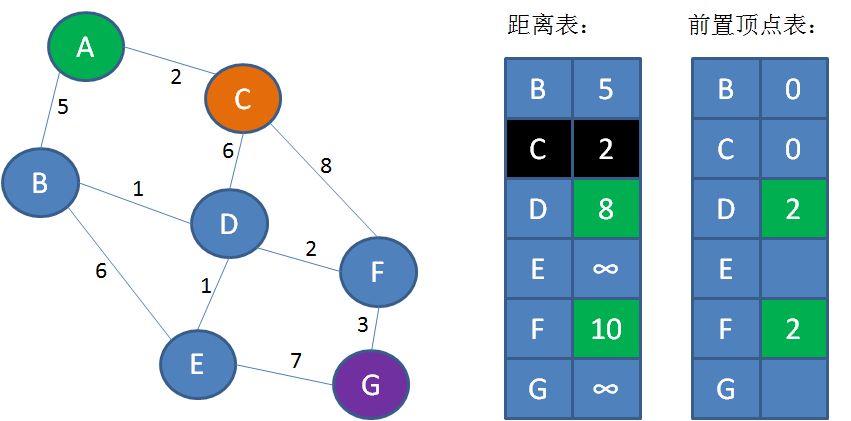
接下来重复第3步、第4步所做的操作：

第5步，也就是第3步的重复，从距离表中找到从A出发距离最短的点(C已经遍历过，不需要考虑)，也就是顶点B。

第6步，也就是第4步的重复，遍历顶点B，找到顶点B的邻接顶点D和E(A已经遍历过，不需要考虑)。从B到D的距离是1，所以A到D的距离是5+1=6，小于距离表中的8；从B到E的距离是6，所以从A到E的距离是5+6=11。把这一信息刷新到表中。

同时，顶点D、E的前置顶点都是B，顶点B在邻接表中下标是1，所以把前置顶点表的D、E值更新为1：

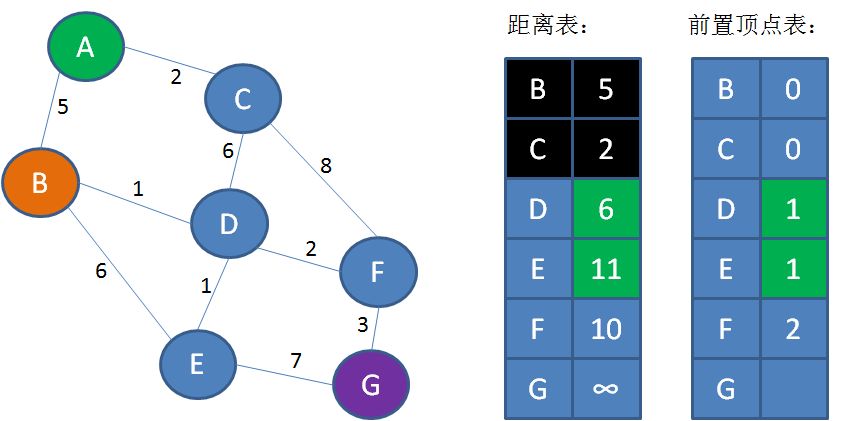
第7步，从距离表中找到从A出发距离最短的点(B和C不用考虑)，也就是顶点D。

第8步，遍历顶点D，找到顶点D的邻接顶点E和F。从D到E的距离是1，所以A到E的距离是6+1=7，小于距离表中的11；从D到F的距离是2，所以从A到F的距离是6+2=8，小于距离表中的10。把这一信息刷新到表中。

同时，顶点E、F的前置顶点都是D，顶点D在邻接表中下标是3，所以把前置顶点表的E、F值更新为3：

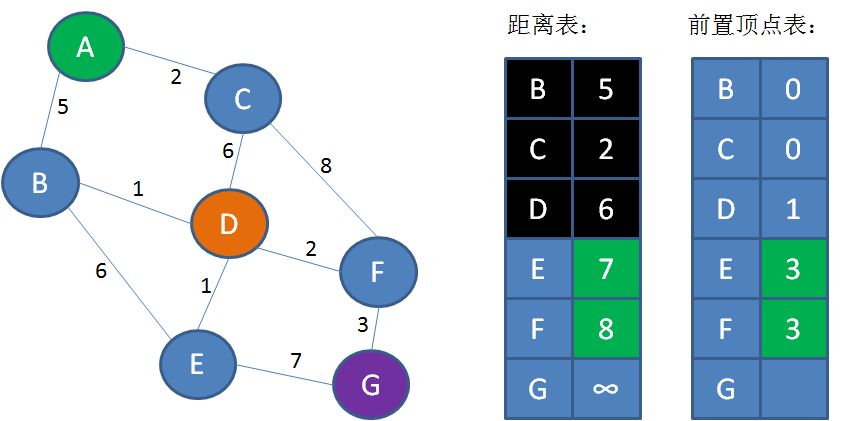
第9步，从距离表中找到从A出发距离最短的点，也就是顶点E。

第10步，遍历顶点E，找到顶点E的邻接顶点G。从E到G的距离是7，所以A到G的距离是7+7=14。把这一信息刷新到表中。

同时，顶点G的前置顶点是E，顶点E在邻接表中下标是4，所以把前置顶点表的G值更新为4：

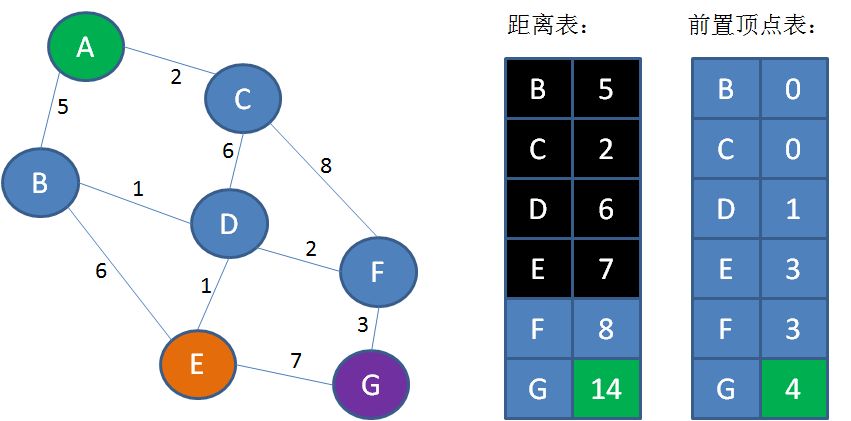
第11步，从距离表中找到从A出发距离最短的点，也就是顶点F。

第12步，遍历顶点F，找到顶点F的邻接顶点G。从F到G的距离是3，所以A到G的距离是8+3=11，小于距离表中的14。把这一信息刷新到表中：

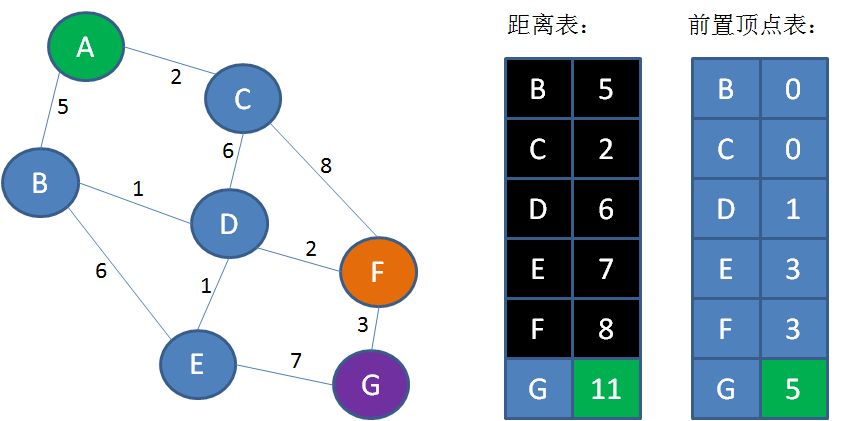
就这样，除终点以外的全部顶点都已经遍历完毕，距离表中存储的是从起点A到所有顶点的最短距离，而前置定点存储的是从起点A到所有顶点最短路径的前置顶点。

如何把前置顶点表“翻译”成图的最短路径呢？我们可以使用回溯法，自后向前回溯：

第1步，找到图的终点G，它是最短路径的终点：

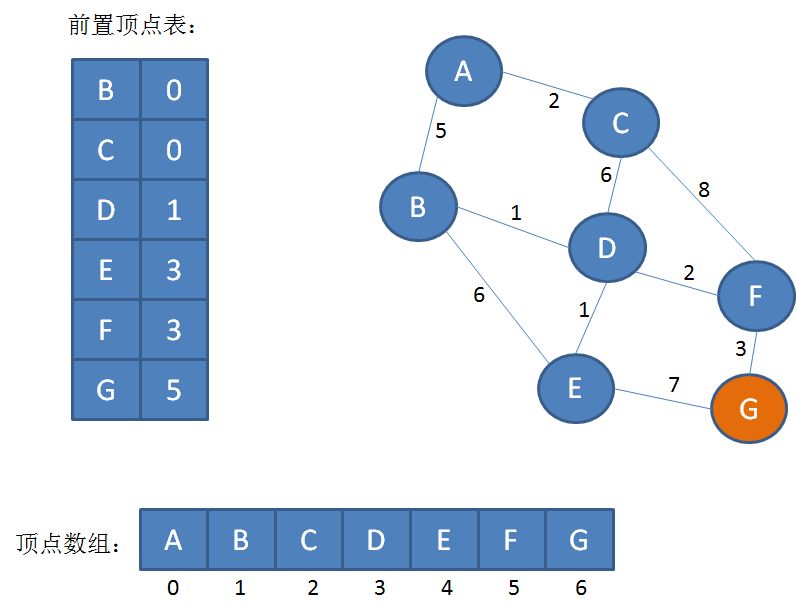
第2步，通过前置定点表找到顶点G对应的前置下标5，在顶点数组中找到下标5对应的顶点F，它是顶点G的前置顶点：

第3步，通过前置定点表找到顶点F对应的前置下标3，在顶点数组中找到下标3对应的顶点D，它是顶点F的前置顶点：

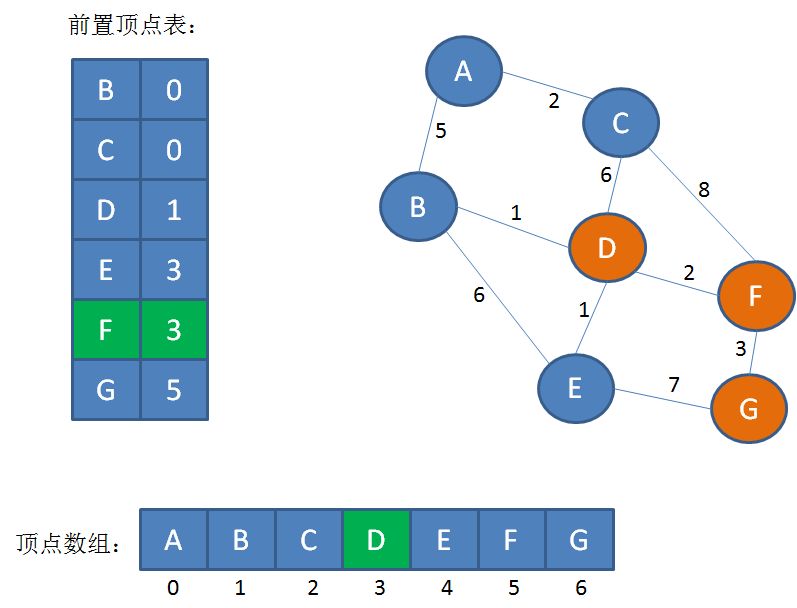
第4步，通过前置定点表找到顶点D对应的前置下标1，在顶点数组中找到下标1对应的顶点B，它是顶点D的前置顶点：

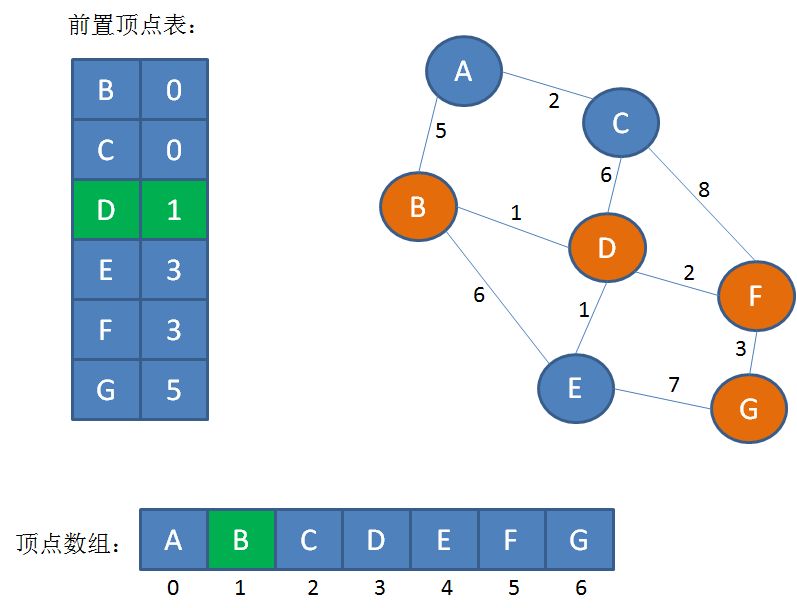
第5步，通过前置定点表找到顶点B对应的前置下标0，在顶点数组中找到下标0对应的顶点A，它是顶点B的前置顶点：

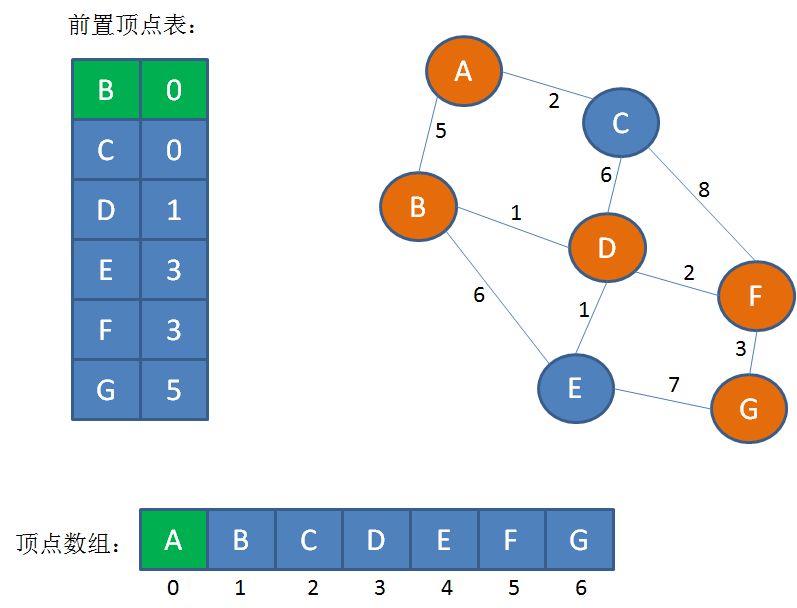
如此一来，我们把前置顶点表(0,0,1,3,3,5)转化成了最短路径(A-B-D-F-G)。

/**

* Dijkstra最短路径算法

*/

public static int[] dijkstra(Graph graph, int startIndex) {

//图的顶点数量

int size = graph.vertexes.length;

//创建距离表，存储从起点到每一个顶点的临时距离

int[] distances = new int[size];

//创建前置定点表，存储从起点到每一个顶点的已知最短路径的前置节点

int[] prevs = new int[size];

//记录顶点遍历状态

boolean[] access = new boolean[size];

//初始化最短路径表，到达每个顶点的路径代价默认为无穷大

for(int i=0; i

distances[i] = Integer.MAX_VALUE;

}

//遍历起点，刷新距离表

access[0] = true;

List<Edge> edgesFromStart = graph.adj[startIndex];

for(Edge edge : edgesFromStart)

{

distances[edge.index] = edge.weight;

prevs[edge.index] = 0;

}

//主循环，重复 遍历最短距离顶点和刷新距离表 的操作

for(int i=1; i

{

//寻找最短距离顶点

int minDistanceFromStart = Integer.MAX_VALUE;

int minDistanceIndex = -1;

for(int j=1; j

{

if(!access[j] && distances[j] < minDistanceFromStart)

{

minDistanceFromStart = distances[j];

minDistanceIndex = j;

}

}

if(minDistanceIndex == -1){

break;

}

//遍历顶点，刷新距离表

access[minDistanceIndex] = true;

for(Edge edge : graph.adj[minDistanceIndex])

{

if(access[edge.index]){

continue;

}

int weight = edge.weight;

int preDistance = distances[edge.index];

if(weight != Integer.MAX_VALUE && (minDistanceFromStart+ weight < preDistance))

{

distances[edge.index] = minDistanceFromStart + weight;

prevs[edge.index] = minDistanceIndex;

}

}

}

return prevs;

}

public static void main(String[] args) {

Graph graph = new Graph(7);

initGraph(graph);

int[] prevs = dijkstra(graph, 0);

printPrevs(graph.vertexes, prevs, graph.vertexes.length-1);

}

private static void printPrevs(Vertex[] vertexes, int[] prev, int i){

if(i>0){

printPrevs(vertexes, prev, prev[i]);

}

System.out.println(vertexes[i].data);

}

/**

* 图的顶点

*/

private static class Vertex {

String data;

Vertex(String data) {

this.data = data;

}

}

/**

* 图的边

*/

private static class Edge {

int index;

int weight;

Edge(int index, int weight) {

this.index = index;

this.weight = weight;

}

}

/**

* 图

*/

private static class Graph {

private Vertex[] vertexes;

private LinkedList<Edge> adj[];

Graph(int size){

//初始化顶点和邻接矩阵

vertexes = new Vertex[size];

adj = new LinkedList[size];

for(int i=0; i

adj[i] = new LinkedList<Edge>();

}

}

}

private static void initGraph(Graph graph){

graph.vertexes[0] = new Vertex("A");

graph.vertexes[1] = new Vertex("B");

graph.vertexes[2] = new Vertex("C");

graph.vertexes[3] = new Vertex("D");

graph.vertexes[4] = new Vertex("E");

graph.vertexes[5] = new Vertex("F");

graph.vertexes[6] = new Vertex("G");

graph.adj[0].add(new Edge(1, 5));

graph.adj[0].add(new Edge(2, 2));

graph.adj[1].add(new Edge(0, 5));

graph.adj[1].add(new Edge(3, 1));

graph.adj[1].add(new Edge(4, 6));

graph.adj[2].add(new Edge(0, 2));

graph.adj[2].add(new Edge(3, 6));

graph.adj[2].add(new Edge(5, 8));

graph.adj[3].add(new Edge(1, 1));

graph.adj[3].add(new Edge(2, 6));

graph.adj[3].add(new Edge(4, 1));

graph.adj[3].add(new Edge(5, 2));

graph.adj[4].add(new Edge(1, 6));

graph.adj[4].add(new Edge(3, 1));

graph.adj[4].add(new Edge(6, 7));

graph.adj[5].add(new Edge(2, 8));

graph.adj[5].add(new Edge(3, 2));

graph.adj[5].add(new Edge(6, 3));

graph.adj[6].add(new Edge(4, 7));

graph.adj[6].add(new Edge(5, 3));

}

代码中，距离表和前置顶点表都是采用数组存储，这样比较方便。

输出最短路径的时候，代码中采用了递归的方式进行回溯。

—————END—————

喜欢本文的朋友们，欢迎长按下图关注公众号程序员小灰，收看更多精彩内容