2个点马氏距离计算实例_多元统计分析——欧式距离和马氏距离

今天介绍一下欧式距离和马氏距离。欧式距离大家都比较熟悉，但是欧式距离在某些情境下不太适用，于是印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出了马氏距离，来解决不能直接使用欧式距离的问题。

文章分为四个部分，第一部分简单介绍欧式距离，第二部分给出不能直接使用欧式距离的例子，第三部分介绍马氏距离，第四部分将欧式距离和马氏距离的优缺点作比较。

欧式距离

欧式距离是指欧几里得空间中两点的直线距离，设p维空间中两点x和y的为：

那么x，y之间的欧式距离可以表示为：

平方欧式距离为：

不能直接使用欧式距离的例子

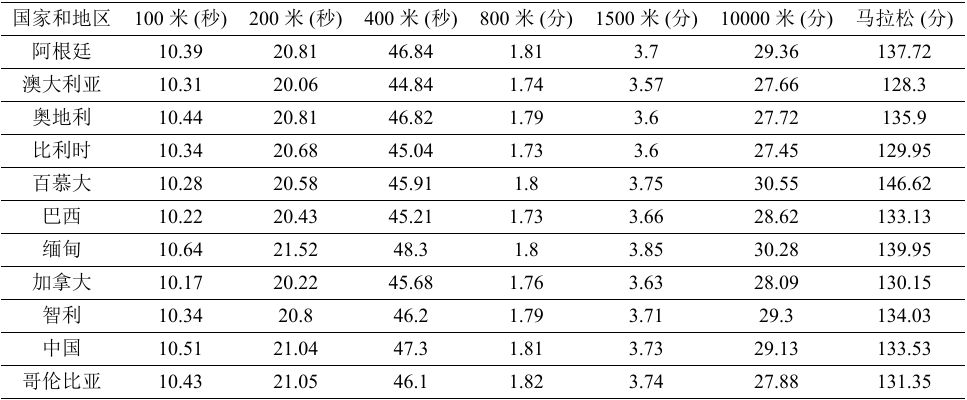
如何判断两国各项目成绩之间的差距？

当我们用欧式距离来比较各国之间田径项目成绩差异的时候，首先要对数据做标准化变换。即每个项目减去各自的均值再除以标准差，这样子可以消除单位和方差差异的影响。但是尽管做到这样，我们发现，有些项目之间有较强的相关性，比如100米和200米成绩的相关性就比较强，在欧式距离的计算中我们不管各个项目之间的相关性，而是给各个分量想相同的权重。这就是欧式距离所忽视的地方，即不能消除各个项目之间相关性的影响。

因此，我们引入了马氏距离。

马氏距离

同样地，设p维空间中两点x，y为：

则x，y之间的马氏距离可表示为：

x到总体的马氏距离可表示为：

其中表示的是x和y的协方差矩阵，由于协方差矩阵的元素表示了各个分量之间的相关性，通过在欧式距离的基础上乘一个协方差矩阵的逆，马氏距离就消除了数据之间相关性的影响。

马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关，同时还可以排除变量之间的相关性的干扰。所以在多用统计分析中一般采用马氏距离。但是，另一方面，马氏距离夸大了微小变量的作用。同时由于马氏距离与协方差矩阵有关，因此协方差矩阵的不确定性往往容易导致无法计算出马氏距离。