两个分布的特征映射_实分析(2)-映射和基数

最新推荐文章于 2024-12-08 12:14:15 发布
最新推荐文章于 2024-12-08 12:14:15 发布
阅读量957 收藏
点赞数
CC 4.0 BY-SA版权
文章标签： 两个分布的特征映射
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_36222664/article/details/113450906
本文探讨映射和基数在集合论中的基本概念，包括映射的定义、Cantor-Bernstein定理、可数集与不可数集的区别、基数的比较以及无最大基数定理。特别地，介绍了如何构造双射以证明集合的势，并讨论了连续基数的性质和连续统假设。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

映射和基数可以说是集合论中最基础的部分，在我看来，映射描述的是两个集合之间的关系而基数描述的是一个集合本身的性质，也就是一个集合元素的多少。如果一个集合是有限集那么很容易用一个特定的自然数来说明集合的元素的多少，但是如果一个集合的元素是无穷多个呢，如何来描述无穷多就成了本文的要点。下面简要说明本文的内容：

  • 映射
    • Cantor-Bernstein定理
  • 集合的势
    • 可数集
    • 不可数集
    • 基数及其比较
  • 重要的例题

这里说明一下为什么不再复习数分中的内容了，其实是在数分中介绍的这部分内容不够全面和仔细并且与实变的内容有一定程度上的重叠，为了内容的完整性和完备性还是以实变的内容为主。

映射

定义2.1（映射）
equation?tex=%5Cforall+x%5Cin+X%2C%5Cexists%21y%5Cin+Y 则称这个对应为映射（变换或者函数）可以记为
equation?tex=f%3A+X%5Cto+Y

关于一个映射我们可以定义该映射下的像集

equation?tex=f%3AX%5Cto+Y%2CA%5Csubset+X 则有
equation?tex=f%28A%29%3D%5C%7By%5Cin+Y%3Ax%5Cin+A%2Cy%3Df%28x%29%5C%7D

下面是像集的一些简单性质

898359dfc308761b2f9168a56459185e.png

同样的我们也可以定义下面的原像集

equation?tex=f%3AX%5Cto+Y%2CB%5Csubset+Y则有
equation?tex=f%5E%7B-1%7D%28B%29%3D%5C%7Bx%5Cin+X%3Af%28x%29%5Cin+B%5C%7D

下面是原像集的一些性质

4748ff8ca1c5f6d7487c83c6489b9af0.png
定义2.2（满射、单射和一一映射）
对于
equation?tex=f%3A+X%5Cto+Y如果

1.
equation?tex=f%28X%29%3DY 则称
equation?tex=f 为满射

2.
equation?tex=%5Cforall+x_1%2Cx_2%5Cin+X%2Cx_1%5Cne+x_2%5CRightarrow+f%28x_1%29%5Cne+f%28x_2%29 则称
equation?tex=f 为单射

3.如果
equation?tex=f 既是满射也是单射那么称其为一一映射

下面介绍复合映射的概念

定义2.3（复合映射）
equation?tex=f%3AX%5Cto+Y%2Cg%3A+Y%5Cto+W 则由
equation?tex=h%28x%29%3Dg%5Bf%28x%29%5D%2C%28x%5Cin+X%29 定义的
equation?tex=h%3A+X%5Cto+W 称为
equation?tex=g%2Cf 的复合映射

下面介绍特征函数，这个函数非常重要学过概率论和数理统计的同学应该知道经验分布函数依概率收敛于总体分布函数。而经验分布函数就是后面提及的简单函数的一个变种，同时简单函数完全是由特征函数的和组成，所以研究好特征函数的性质至关重要。

6c7d277473e6e76456c5d269fa82119c.png

下面是特征函数的性质

  1. equation?tex=%5C%28+%5Cchi+_%7BA%5Ccup+B%7D%3D%5Cchi+_A%2B%5Cchi+_B-%5Cchi+_%7BA%5Ccap+B%7D+%5C%29+
  2. equation?tex=%5C%28+%5Cchi+_%7BA%5Ccap+B%7D%3D%5Cchi+_A%C2%B7%5Cchi+_B+%5C%29+
  3. equation?tex=%5C%28+%5Cchi+_%7BA%5Csetminus+B%7D%3D%5Cchi+_A%5Cleft%5B+1-%5Cchi+_B+%5Cright%5D++%5C%29+++
  4. equation?tex=%5C%28+%5Cchi+_%7BA%5CDelta+B%7D%3D%7C%5Cchi+_A-%5Cchi+_B%7C+%5C%29+

除此之外还有一个跟上下极限、上下限集相关的结论：

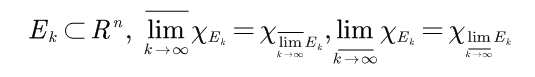
78d1a788cc8c87a9e08fe7ed558b37cf.png
定理2.1（单调映射的不动点）
equation?tex=X 非空，且
equation?tex=f%3A+%5Cmathscr%7BP%7D%5Cleft%28+X+%5Cright%29+%5Crightarrow+%5Cmathscr%7BP%7D%5Cleft%28+X+%5Cright%29+++ 若对任意
equation?tex=A%2CB%5Cin%5Cmathscr%7BP%7D%28X%29%2CA%5Csubset+B 有
equation?tex=f%28A%29%5Csubset+f%28B%29 则存在
equation?tex=T%5Cin%5Cmathscr%7BP%7D%28X%29 使得
equation?tex=f%28T%29%3DT
  • 作集合
    equation?tex=S%3D%5C%7BA%3AA%5Cin%5Cmathscr%7BP%7D%28X%29%2CA%5Csubset+f%28A%29%5C%7D%2CT%3D%5Cbigcup_%7BA%5Cin+S%7DA%5Cin%5Cmathscr%7BP%7D%28X%29
  • 只用证明
    equation?tex=T%3Df%28T%29 即可
定义2.3（分离集）
存在
equation?tex=X%2CY 之间的映射
equation?tex=f%3AX%5Cto+Y%2Cg%3AY%5Cto+X，
equation?tex=E%5Csubset+X 为分离集则
equation?tex=E%5Ccap+g%28Y%5Csetminus+f%28E%29%29%3D++%5Coslash+++++

下面介绍两个个引理，由这个引理可以导出后面重要的C-B定理

引理2.1
equation?tex=X 中的分离集为
equation?tex=%5CGamma ，
equation?tex=A%3D%5Cbigcup_%7BE%5Cin%5CGamma%7DE 为
equation?tex=%5CGamma 中的最大元
引理2.2（集合在映射下的分解）
如果有
equation?tex=f%3AX%5Cto+Y%2Cg%3A+Y%5Cto+X 则存在分解
equation?tex=X%3DA%5Ccup%5Cbar%7BA%7D%2CY%3DB%5Ccup%5Cbar%7BB%7D 其中
equation?tex=f%28A%29%3DB%2Cg%28%5Cbar%7BB%7D%29%3D%5Cbar%7BA%7D%2CA%5Ccap%5Cbar%7BA%7D%3D%5Coslash%2CB%5Ccap%5Cbar%7BB%7D%3D%5Coslash

根据上面两个引理可以轻松推出Cantor-Bernstein定理

定理2.2（Cantor-Bernstein定理）
若集合
equation?tex=X%2CY 的某个真子集对等，
equation?tex=Y%2CX 的某个真子集对等，则
equation?tex=X%5Csim+Y
  • 由定理2.2可以知道
    equation?tex=X%3DA%5Ccup%5Cbar%7BA%7D%2CY%3DB%5Ccup%5Cbar%7BB%7D 且
    equation?tex=f%28A%29%3DB%2Cg%28%5Cbar%7BB%7D%29%3D%5Cbar%7BA%7D%2CA%5Ccap%5Cbar%7BA%7D%3D%5Coslash%2CB%5Ccap%5Cbar%7BB%7D%3D%5Coslash
  • 则构造双射
    equation?tex=%5C%28+F%5Cleft%28+x+%5Cright%29+%3D%5Cleft%5C%7B+%5Cbegin%7Barray%7D%7Bl%7D+%09f%5Cleft%28+x+%5Cright%29+%2C%5C+x%5Cin+A%5C%5C+%09g%5E%7B-1%7D%5Cleft%28+x+%5Cright%29+%2C%5C+x%5Cin+%5Cbar%7BA%7D%5C%5C+%5Cend%7Barray%7D+%5Cright.++%5C%29+ 即可得证

集合的势

定义2.4
设
equation?tex=A%2CB 是两个集合，如果
equation?tex=A%5Csim+B 则我们说这两个集合等势

基数的概念是有限个元素个数的一个推广，它反映出一切对等集所仅有的共性（数量属性）

自然数集

equation?tex=%5Cmathbb%7BN%7D 的基数——可数集

我们记自然数集

equation?tex=%5Cmathbb%7BN%7D 的基数为
equation?tex=%5Caleph_0 ,集合
equation?tex=A%5Csim%5Cmathbb%7BN%7D%5CLeftrightarrow+%7CA%7C%3D%5Caleph_0

下面有几个性质

  • equation?tex=%5Cmathbb%7BZ%7D%5Csim%5Cmathbb%7BQ%7D%5Csim%5Cmathbb%7BN%7D
  • 任意无限集合
    equation?tex=E 必包含一个可数集
  • equation?tex=A_n%2Cn%3D1%2C2%2C... 为可数集，则
    equation?tex=A%3D%5Cbigcup_%7Bn%3D1%7D%5E%7B%5Cinfty%7DA_n 为可数集
  • equation?tex=A_n%2Cn%3D1%2C2%2C... 为可数集，则
    equation?tex=A_1%5Ctimes+A_2%5Ctimes...%5Ctimes+A_n 为可数集

性质1和性质3的构造借助了图论的思想（对角线方法），有兴趣的读者可以参考下面的链接

http://en.wikipedia.org/wiki/Cardinal_number​en.wikipedia.org

下面的几个例子是对上述的性质的一个简单应用

例2.1

equation?tex=R%5E1 中互不相交的区间是可数集

例2.2

equation?tex=R%5E1 上单调函数的不连续点是可数集
  • 以单增函数
    equation?tex=f%28x%29 的不连续点
    equation?tex=x_0 为例
  • 每个不连续点
    equation?tex=x_0 对应一个区间
    equation?tex=%28f%28x_0%29-0%2Cf%28x_0%29%2B0%29 同时运用例2.1即可得出结论

例2.3

设

equation?tex=E%5Csubset+R%5E1 是可数集，则存在
equation?tex=x_0%5Cin+R%5E1 使得
equation?tex=E%5Ccap%28E%2B%5C%7Bx_0%5C%7D%29%3D%5Coslash
  • 令
    equation?tex=E%3D%5C%7Br_n%5C%7D 作
    equation?tex=A%3D%5C%7Br_n-r_m%3An%5Cne+m%5C%7D
  • 因为
    equation?tex=A 是可数集，则存在
    equation?tex=R%5E1 中点
    equation?tex=x_0 满足
    equation?tex=x_0%5Cne+r_n-r_m%2C+%28n%5Cne+m%3Bn%2Cm%3D1%2C2%2C...%29
  • 即
    equation?tex=r_n%5Cne+r_m%2Bx_0 得证

equation?tex=R%5E1 的基数——不可数集

由一一映射

equation?tex=f%28x%29%3D%5Cfrac%7B2%7D%7B%5Cpi%7Darctanx 知
equation?tex=R%5E1%5Csim+%5B-1%2C1%5D ，再由一一映射
equation?tex=f%28x%29%3D%5Cfrac%7Bx%2B1%7D%7B2%7D 知
equation?tex=%5B-1%2C1%5D%5Csim%5B0%2C1%5D 所以我们仅用研究
equation?tex=%5B0%2C1%5D 的基数即可
定理2.3
区间
equation?tex=%5B0%2C1%5D%3D%5C%7Bx%3A0%5Cle+x%5Cle1%5C%7D 不是可数集

这个定理在这里也不详细证明了，提供两种思路：

  • 利用反证法+对角线方法证明
  • 证明
    equation?tex=%5B0%2C1%5D 的基数和
    equation?tex=%5Cmathbb%7BN%7D 的幂集的基数相等

我们称

equation?tex=%5B0%2C1%5D 的基数为连续基数，记为
equation?tex=c%28%E6%88%96%5Caleph_1%29 ,由上面的描述可以知道
equation?tex=%7CR%5E1%7C%3Dc

同样的我们有下面的一些性质

  • equation?tex=A_n%2Cn%3D1%2C2%2C... 的基数为连续基数，则
    equation?tex=A%3D%5Cbigcup_%7Bn%3D1%7D%5E%7B%5Cinfty%7DA_n 的基数为连续基数
  • equation?tex=A_n%2Cn%3D1%2C2%2C... 的基数为连续基数，则
    equation?tex=A_1%5Ctimes+A_2%5Ctimes...%5Ctimes+A_n 的基数为连续基数

结合上面的一些性质我们可以得到下面这个更加普遍的结论

对于

equation?tex=%5Cbigcup_%7B%5Calpha%5Cin+E%7DA_%5Calpha 只有在
equation?tex=E%2C%5Cforall+A_%5Calpha 都至多可数时才至多可数，否则不可数

下面引出一个关于闭区间上连续函数的例题

例2.4

区间

equation?tex=%5Ba%2Cb%5D 上的连续函数全体
equation?tex=C%5Ba%2Cb%5D 的基数为
equation?tex=c
  • 常函数是连续函数则
    equation?tex=R%5E1 和
    equation?tex=C%5Ba%2Cb%5D 的一个子集对等，则
    equation?tex=%7CC%5Ba%2Cb%5D%7C%5Cge+c
  • 通过构造单射
    equation?tex=f%28%5Cvarphi%29%3D%5C%7B%28s%2Ct%29%5Cin%5Cmathbb%7BQ%7D%5Ctimes%5Cmathbb%7BQ%7D%3As%5Cin%5Ba%2Cb%5D%2Ct%5Cle%5Cvarphi%28s%29%5C%7D 且
    equation?tex=f%3AC%5Ba%2Cb%5D%5Cto+%5Cmathscr%7BP%7D%28%5Cmathbb%7BQ%5E2%7D%29++ ,则
    equation?tex=%7CC%5Ba%2Cb%5D%7C%5Cle%5Cmathscr%7BP%7D%28%5Cmathbb%7BQ%5E2%7D%29%3Dc
  • 综上所述
    equation?tex=%7CC%5Ba%2Cb%5D%7C%3Dc

最后我们介绍无最大基数定理

定理2.4（无最大基数定理）
若
equation?tex=A 为非空集合，则
equation?tex=A 与其幂集
equation?tex=%5Cmathscr%7BP%7D%28A%29 不对等
  • 利用反证法，构造
    equation?tex=A 到
    equation?tex=%5Cmathscr%7BP%7D%28A%29上的一一映射
    equation?tex=f
  • 作集合
    equation?tex=B%3D%5C%7Bx%5Cin+A%3Ax%5Cnotin+f%28x%29%5C%7D
    • 若
      equation?tex=y%5Cin+B 则
      equation?tex=y%5Cnotin+f%28y%29%3DB
    • 若
      equation?tex=y%5Cnotin+B 则
      equation?tex=y%5Cin+f%28y%29%3DB
    • 矛盾，即得证

这个证明非常的巧妙，充分利用了幂集的特点，是一个非常经典的反证法的应用。

最后再提一嘴连续统假设

我们从上面集合基数的讨论中可以发现

equation?tex=%5Cmathbb%7BN%7D 的基数为
equation?tex=%5Caleph_0 ，
equation?tex=%5Cmathbb%7BR%7D 的基数为
equation?tex=%5Caleph_1 但是在它们之间是否存在其他的基数呢？这就是连续统假设要研究的问题。有兴趣的读者可以搜搜看，毕竟这个也是数学界皇冠上的珍珠之一。
20、数据库分析：增强实体 - 关系模型详解
kk1234的博客
05-20 38
本文深入探讨了数据库分析中的增强实体-关系（EER）模型，涵盖了超类型/子类型关系、实体聚类、打包数据模型等核心概念。文章详细解析了EER模型的扩展特性，如泛化、特化、完整性约束和不相交/重叠规则，并通过多个实际问题示例（如租车管理、银行账户、非营利组织人员管理等）展示了如何构建和应用EER模型。此外，文章还讨论了打包数据模型的应用价值与挑战，以及数据剖析在数据建模中的作用，为数据库设计人员提供了全面的理论指导和实践参考。
MySql (四) ER图与实体关系映射
UNIQUE_XIAOXI的博客
10-07 5698
目标：掌握ER图的画法。 ERMaster 初步掌握数据库设计的方法 实体关系映射什么是数据库的设计？数据库设计(Database Design)是指对于一个给定的应用环境，构造最优的数据库模式，建立数据库及其应用系统，使之能够有效地存储数据，满足各种用户的应用需求（信息要求和处理要求）。 数据开发步骤： 那么：我们的数据库设计是不是可以理解为：实体模型 ->概念模型->数据模型的过程。 数据库设
两个分布的特征映射_简单的数据预处理和特征工程
weixin_28692867的博客
01-30 1204
一、归一化和KD数1>为什么要归一化在实际应用中，样本的不同特征的单位不同，会在求距离时造成很大的影响。在量纲不同的情况下，不能反映样本中每一个特征的重要程度，所以我们需要对数据归一化处。2>解决归一化问题通常解决措施是把所有的数据都映射到同一个尺度（量纲）上。3>常见归一化方法最值归一化(normalization)：把所有数据映射到0-1之间。最值归一化的使用范围是特征的分布...
两个分布的特征映射_跨语言分布表示学习方法概述
weixin_31115971的博客
01-15 558
分布表示(distributed representation)与深度神经网络(deep neural network)极大地推动了近几年自然语言处理研究的发展。我们知道，分布表示指的是对于一个客观描述对象的低维、稠密、连续向量表示。不同于符号表示(symbolic representation)，分布表示可以自然地联结表现形式不同但语义空间相同(或相似)的对象，比如不同模态数据(图像、文本、语音...
图形学数学基础之采样分布映射
i_dovelemon的专栏
02-03 2495
作者：idovelemon 日期：2018-02-03 来源：优快云 主题：Sampling,Distribution,PDF, MDF, CDF, Inverse Method 引言 如果你尝试过自己去实现一些Image Based Lighting或者Path Tracer等需要解决渲染方程积分问题算法的时候，你就会发现一个你绕不开的概念：Monte Carlo Impo
Hibernate基数映射
hippoppower的专栏
10-04 1568
一对一两种方式:   唯一外键  共享主键 唯一外键  用外键的形式  再把外键设成unique="true" 共享主键                     acct           user想用Account的主键 user.setAcct(acct);//自动级联的条件(user想用account的主键)--user必须要能看到accts.save(us
数据的分布和映射
2301_77061654的博客
12-08 1601
数据分布描述了数据在不同取值区间的散布情况，它可以帮助我们了解数据的集中程度、离散程度、对称性等重要特征。这些信息对于数据清洗、特征选择、模型构建等数据处理和分析环节至关重要。常见的数据分布包括均匀分布、泊松分布、正态分布等。
Stein实分析学习笔记
06-11
两个集合如果具有相同基数，意味着它们之间存在一一对应关系。实数集的基数是不可计算的，表示它比任何可数集合（如自然数集）都要大。 通过这些基本概念和定理，Stein实分析笔记为我们构建了一个理解实数系统及其...
云客Drupal源码分析之内容实体数据库表结构及表映射table mapping
云客的技术博客【云游天下 做客四方】
11-24 1636
“字段”概念 在drupal中提到“字段”这个概念时，请不要理解为数据库中表的一个列，这不是一个概念，它是指一个字段对象，充当着实体对象的属性，也是一个列表类型的类型化数据对象，当本系列提到“字段field”一般均是指字段对象或字段定义对象，而数据库表中的字段列，则将其称为“列column”；一个字段对象可以包含数据库表中的多个列（取决于字段类型定义中的schema），这些列称为字段对象的属性，
erDiagram USER ||--o{ ORDER : "下单(1:N)" USER ||--o{ FEEDBACK : "提交(1:N)" USER }|--|| DINING_TABLE : "服务(N:1)" DISH_CATEGORY ||--o{ DISH : "包含(1:N)" ORDER }|--|| DINING_TABLE : "占用(1:1)" ORDER }|--|| USER : "服务(服务员)(N:1)" ORDER ||--o{ ORDER_DETAIL : "包含(1:N)" ORDER ||--|| PAYMENT : "关联(1:1)" ORDER ||--|| FEEDBACK : "对应(1:1)" DISH }o--|| ORDER_DETAIL : "被订购(N:M)" ORDER_DETAIL }|--|| DISH : "明细(1:1)"将这个转化为E-R图
最新发布
06-08
实际上，第一个是DISH和ORDER_DETAIL的多对多，第二个是ORDER_DETAIL和DISH的一对一，但这两个描述是同一个关系。因此，我们以最后一个描述为准（即一对一），因为最后一个描述指定了ORDER_DETAIL到DISH是一对一。...
均匀分布映射到任意分布
https://www.cnblogs.com/qizhou/
04-11 1741
　　当我们想对某些特定分布进行抽样时，要通过均匀分布的抽样来映射，因为电脑算法产生的伪随机数是看做均匀分布的。 　　假设均匀分布随机变量为$X$，则特定分布$\displaystyle p_Y(y)$的随机变量就为$Y=g(X)$。如何求得这个$g(x)$映射呢？ 　　关于利用均匀分布随机变量产生任意分布变量的实现 - Rainlin - 博客园 　　虽然这个博客有一些借鉴意义，但是我觉...
数据库表与表之间关系的映射基数
Lzzzzzzk的博客
03-02 642
数据库表与表之间关系的映射基数,SQL命令
人工智能数学基础：两个存在映射关系的随机变量的概率密度函数关系研究
老猿Python
08-23 3710
本文介绍了两个存在映射关系的随机变量的概率密度函数之间的关系，并利用概率论和微积分的相关知识介绍了推导过程。
如何设计ER图（映射基数）
k的博客
04-04 6698
映射基数 第一种 1一对一：一个导师最多指导一个学生，一个学生最多被一个导师指导。 说明导师可以不指导学生，学生也可以单干。 2.多对多：一个导师可以指导任意学生，一个学生可以被任意多个导师指导。 说明导师可以不指导学生，也可以指导好些个。学生可以单干，也可以多拜几个师傅 3. 一对多：一个导师可以指导任意多个学生，一个学生至多被一个导师指导。 多对一：一个导师至多指导一个学生，一个学...
两个分布的特征映射_三大抽样分布定理——未验证的证明
weixin_39775354的博客
01-07 297
三大抽样分布定理是数理统计的中心所在，各种统计量围绕他来展开。我把三大抽样分布定理放在代数（正交变换和二次型）的视角下，可能会给大家提供一种不同的思路和角度。由于我只学过高代，而且最近才把高代复习完一遍，更深层次的代数结构我是不太懂的，所以大家有什么意见可以在下面留言，我们一起交流啊！！谢谢大家！！--------------------------------------------------...
“强化学习说白了，是建立分布到分布之间的映射”？数学角度谈谈个人观点
记录学习痕迹的公众号：Piper蛋窝
10-27 1328
“强化学习说白了，是建立分布到分布之间的映射。” 我从没有听过别人提这样的观点，这让我静下心来，去再次思考强化学习的数学假设。 我将在此对这个观点进行分析。
深度子领域自适应的方法（DSAN）「迁移学习」「AI核心算法」
热门推荐
九三智能控
11-13 1万+
关注：决策智能与机器学习，深耕AI脱水干货作者：朱勇椿 来源：王晋东不在家（ID：yourwjd）转载请联系作者本期我们将为大家介绍一种极为简单的「深度子领域自适应的方法（DSAN）」...
图论算法总结（二）
qq_43632898的博客
05-22 550
讲完了图论，说实话，没听懂，我也只能捡着我听懂的部分写一下。 并查集是一种用于分离集合操作的抽象数据类型。它所处理的是“集合”之间的关系，即动态地维护和处理集合元素之间复杂的关系，当给出两个元素的一个无序对(a,b)时，需要快速“合并”a和b分别所在的集合，这其间需要反复“查找”某元素所在的集合。“并”、“查”和“集”三字由此而来。在这种数据类型中，n个不同的元素被分...
算法基础期末考点总结十八——分离集合数据结构
weixin_43416013的博客
01-15 405
这里笔者不是很熟悉，老师是在讲图算法的时候，返回来讲到这里的。 基本操作 建立新集合 合并集合 找到包含x的集合的根 在编译原理实验中，就有关于集合操作的代码。 链表操作 这是集合链表的大概图示，发现每个操作摊还代价为O(n)。 当我记录集合大小后，每次合并都把小的集合并到大集合中，发现m个操作序列的时间复杂度变为O(m+nlgn)（n为创建集合的次数） 不相交集合森林 如果集合不相交，我们用根树来表示集合。 引入两种启发式策略： 1.按秩合并 就是把小树的根指向大树的根，来进行集合的合并 2.路径压缩
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值