机器学习2-回归算法

最新推荐文章于 2025-03-18 22:34:40 发布

Chise1

最新推荐文章于 2025-03-18 22:34:40 发布

阅读量499

点赞数

CC 4.0 BY-SA版权

分类专栏： python 文章标签：机器学习

本文链接：https://blog.youkuaiyun.com/weixin_36179862/article/details/84979088

python 专栏收录该内容

57 篇文章

订阅专栏

文章目录

线性回归和梯度下降算法
岭回归
- Ridge
- RidgeCV
Lasso 套索
多项式回归

线性回归和梯度下降算法

机器学习的基本问题

回归问题：由已知的分布于连续域中的输入和输出，通过不断地模型训练，找到输入和输出之间的联系，通常这种联系可以通过一个函数方程被形式化，如：y=w0+w1x+w2x^2…，当提供未知输出的输入时，就可以根据以上函数方程，预测出与之对应的连续域输出。
分类问题：如果将回归问题中的输出从连续域变为离散域，那么该问题就是一个分类问题。
聚类问题：从已知的输入中寻找某种模式，比如相似性，根据该模式将输入划分为不同的集群，并对新的输入应用同样的划分方式，以确定其归属的集群。
降维问题：从大量的特征中选择那些对模型预测最关键的少量特征，以降低输入样本的维度，提高模型的性能。

一元线性回归

预测函数

输入输出
0 1
1 3
2 5
3 7
4 9
…
y=1+2 x
10 -> 21
y=w0+w1x
任务就是寻找预测函数中的模型参数w0和w1，以满足输入和输出之间的联系。

预测函数： y=w0 +w1x
xm ->ym'   =   w0+w1xm ym   (ym-y'm)^2
           |                               |             |
   预测输出                 实际输出       单样本误差
   总样本误差：
   (y1'-y1)^2+(y2'-y2)^2+......+(ym'-ym)^2
   ---------------------------------------------------------=E
                    2(除以2的目的是微分的时候约掉2)
损失函数：E=Loss(w0,w1)
损失函数体现了总样本误差即损失值随着模型参数的变化而变化

梯度下降法寻优

推导：
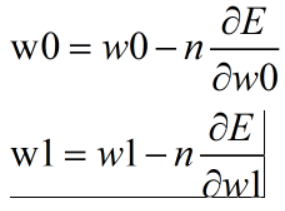
在这里插入图片描述
计算损失函数在该模型参数处的梯度<-+
计算与该梯度反方向的修正步长 |
[-nDLoss/Dwo, -nDLoss/Dw1] |
计算下一组模型参数 |
w0=w0-nDLoss/Dw0 |
w1=w1-nDLoss/Dw1---------------+
直到满足迭代终止条件：
迭代足够多次；
损失值已经足够小；
损失值已经不再明显减少。
由于：
在这里插入图片描述
python代码：

import numpy as np
import matplotlib.pyplot as mp
from mpl_toolkits.mplot3d import axes3d
train_x = np.array([0.5, 0.6, 0.8, 1.1, 1.4])
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0])
# 迭代次数
n_epoches = 1000
# 学习率
lrate = 0.01
epoches, losses = [], []
w0, w1 = [1], [1]
# 迭代一千次
for epoch in range(1, n_epoches + 1):
    # 记录样本误差的步数
    epoches.append(epoch)
    # 求总样本误差
    losses.append(((train_y - (
        w0[-1] + w1[-1] * train_x)) ** 2 / 2).sum())
    print('{:4}> w0={:.8f}, w1={:.8f}, loss={:.8f}'.format(
        epoches[-1], w0[-1], w1[-1], losses[-1]))
    d0 = -(train_y - (w0[-1] + w1[-1] * train_x)).sum()
    d1 = -((train_y - (w0[-1] + w1[-1] * train_x)) * train_x).sum()
    w0.append(w0[-1] - lrate * d0)
    w1.append(w1[-1] - lrate * d1)
w0 = np.array(w0[:-1])
w1 = np.array(w1[:-1])
sorted_indices = train_x.argsort()
test_x = train_x[sorted_indices]
test_y = train_y[sorted_indices]
pred_test_y = w0[-1] + w1[-1] * test_x
grid_w0, grid_w1 = np.meshgrid(
    np.linspace(0, 9, 500),
    np.linspace(0, 3.5, 500))
flat_w0, flat_w1 = grid_w0.ravel(), grid_w1.ravel()
flat_loss = (((flat_w0 + np.outer(
    train_x, flat_w1)) - train_y.reshape(
    -1, 1)) ** 2).sum(axis=0) / 2
grid_loss = flat_loss.reshape(grid_w0.shape)
mp.figure('Linear Regression', facecolor='lightgray')
mp.title('Linear Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(train_x, train_y, marker='s',
           c='dodgerblue', alpha=0.5, s=80,
           label='Training')
mp.scatter(test_x, test_y, marker='D',
           c='orangered', alpha=0.5, s=60,
           label='Testing')
mp.scatter(test_x, pred_test_y, c='orangered',
           alpha=0.5, s=60, label='Predicted')
for x, y, pred_y in zip(
        test_x, test_y, pred_test_y):
    mp.plot([x, x], [y, pred_y], c='orangered',
            alpha=0.5, linewidth=1)
mp.plot(test_x, pred_test_y, '--', c='limegreen',
        label='Regression', linewidth=1)
mp.legend()
mp.figure('Training Progress', facecolor='lightgray')
mp.subplot(311)
mp.title('Training Progress', fontsize=20)
mp.ylabel('w0', fontsize=14)
mp.gca().xaxis.set_major_locator(
    mp.MultipleLocator(100))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(epoches, w0, c='dodgerblue', label='w0')
mp.legend()
mp.subplot(312)
mp.ylabel('w1', fontsize=14)
mp.gca().xaxis.set_major_locator(
    mp.MultipleLocator(100))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(epoches, w1, c='limegreen', label='w1')
mp.legend()
mp.subplot(313)
mp.xlabel('epoch', fontsize=14)
mp.ylabel('loss', fontsize=14)
mp.gca().xaxis.set_major_locator(
    mp.MultipleLocator(100))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(epoches, losses, c='orangered', label='loss')
mp.legend()
mp.tight_layout()
mp.figure('Loss Function')
ax = mp.gca(projection='3d')
mp.title('Loss Function', fontsize=20)
ax.set_xlabel('w0', fontsize=14)
ax.set_ylabel('w1', fontsize=14)
ax.set_zlabel('loss', fontsize=14)
mp.tick_params(labelsize=10)
ax.plot_surface(grid_w0, grid_w1, grid_loss,
                rstride=10, cstride=10, cmap='jet')
ax.plot(w0, w1, losses, 'o-', c='orangered',
        label='BGD')
mp.legend()
mp.figure('Batch Gradient Descent',
          facecolor='lightgray')
mp.title('Batch Gradient Descent', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.contourf(grid_w0, grid_w1, grid_loss, 1000,
            cmap='jet')
cntr = mp.contour(grid_w0, grid_w1, grid_loss, 10,
                  colors='black', linewidths=0.5)
mp.clabel(cntr, inline_spacing=0.1, fmt='%.2f',
          fontsize=8)
mp.plot(w0, w1, 'o-', c='orangered', label='BGD')
mp.legend()
mp.show()

线性回归器

import sklearn.linear_model as lm 线性回归回归器的引入
线性回归器 = lm.LinearRegression()
线性回归器.fit(已知输入, 已知输出) # 计算模型参数
线性回归器.predict(新的输入)->新的输出
import sklearn.metrics as sm该模块主要用于计算误差值？

import numpy as np
import sklearn.linear_model as lm
import sklearn.metrics as sm
import matplotlib.pyplot as mp
# 采集数据
x, y = [], []
with open(r'C:\Users\Cs\Desktop\机器学习\ML\data\single.txt', 'r') as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(',')]
        x.append(data[:-1])
        y.append(data[-1])
x = np.array(x)
y = np.array(y)
# 创建线型回归器模型：
model = lm.LinearRegression()
# 训练模型
model.fit(x, y)
# 根据输入预测输出
pred_y = model.predict(x)
# 输出实际值
mp.figure("ML")
mp.xlabel('x1', fontsize=20)
mp.ylabel('y1')

mp.scatter(x, y, label="truth", c="blue")
mp.plot(x, pred_y, label="model", c="orange")
print("标准差：", np.std(y-pred_y, ddof=1))
# 衡量误差，R2得分，将误差从[0,+∞)误差映射到[1,0)，越接近1，越好，越接近0，越差。
# 去掉了参数量级对误差的影响
print("r2:", sm.r2_score(y, pred_y))
# 其他误差求解，大多都受参数量级影响：
# sm.coverage_error
# sm.mean_absolute_error
# sm.mean_squared_error
# sm.mean_squared_log_error
# sm.median_absolute_error
# sm.explained_variance_score
mp.legend()
mp.show()

模型的转储与载入

模型的转储与载入：pickle
将内存对象存入磁盘或者从磁盘读取内存对象。
import pickle
存入：pickle.dump
读取： pickle.load

# 保存，注意是二进制格式
with open('线性回归.pkl','wb') as f:
   pickle.dump(model,f)
# 读取
with open('..pkl','rb') as f:
model=pickle.load(f)

岭回归

Ridge

Loss(w0, w1)=SIGMA[1/2(y-(w0+w1x))^2]
+正则强度 * f(w0, w1)
普通线性回归模型使用基于梯度下降的最小二乘法，在最小化损失函数的前提下，寻找最优模型参数，于此过程中，包括少数异常样本在内的全部训练数据都会对最终模型参数造成程度相等的影响，异常值对模型所带来的影响无法在训练过程中被识别出来。为此，岭回归在模型迭代过程所依据的损失函数中增加了正则项，以限制模型参数对异常样本的匹配程度，进而提高模型对多数正常样本的拟合精度。
岭回归：model2 = lm.Ridge(300, fit_intercept=True)
第一个参数(300)越大，最后拟合效果收异常影响越小，但是整体数据对拟合线也越小。所以这个值需要好好测试。
拟合：lm.fit(x,y)
model2 = lm.Ridge(300, fit_intercept=True)
fit_intercept:如果为True，有节距，为False，则过原点，默认为true

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
x, y = [], []
with open(r'C:\Users\Cs\Desktop\机器学习\ML\data\abnormal.txt', 'r') as f:
    for line in f.readlines():
        data = [float(substr) for substr
                in line.split(',')]
        x.append(data[:-1])
        y.append(data[-1])
x = np.array(x)
y = np.array(y)
model1 = lm.LinearRegression()
model1.fit(x, y)
pred_y1 = model1.predict(x)
model2 = lm.Ridge(300, fit_intercept=True)
model2.fit(x, y)
pred_y2 = model2.predict(x)
mp.figure('Linear & Ridge Regression',
          facecolor='lightgray')
mp.title('Linear & Ridge Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(x, y, c='dodgerblue', alpha=0.75, s=60,
           label='Sample')
sorted_indices = x.ravel().argsort()
mp.plot(x[sorted_indices], pred_y1[sorted_indices],
        c='orangered', label='Linear')
mp.plot(x[sorted_indices], pred_y2[sorted_indices],
        c='limegreen', label='Ridge')
mp.legend()
mp.show()

RidgeCV

Ridge的升级版，通过一次输入多个正则强度，返回最优解。
使用方法：

reg=RidgeCV(alphas=[1,2,3],fit_intercept=True)
#或：reg=RidgeCV([1,2,3])
reg.alpha_#获取权重

Lasso 套索

Lasso：使用结构风险最小化=损失函数（平方损失）+正则化（L1范数）

多项式回归

将一元的多项式回归，变成多元的线性回归。每一个不同的x^n都视作一个元

多元线性：    y=w0+w1x1+w2x2+w3x3+...+wnxn
                       ^ x1 = x^1
                        | x2 = x^2
                        | ...
                        | xn = x^n

一元多项式：y=w0+w1x+w2x^2+w3x^3+...+wnx^n
用多项式特征扩展器转换，用线型回归器训练。
x->多项式特征扩展器 -x1...xn-> 线性回归器->w0...wn
      \______________________________________/
                                   管线

代码：

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import sklearn.pipeline as pl
import sklearn.preprocessing as sp
import sklearn.linear_model as lm
import sklearn.metrics as sm
import matplotlib.pyplot as mp

train_x, train_y = [], []
with open(r'C:\Users\Cs\Desktop\机器学习\ML\data\single.txt', 'r') as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(',')]
        train_x.append(data[:-1])
        train_y.append(data[-1])
train_x = np.array(train_x)
train_y = np.array(train_y)
# sp.PolynomialFeatures(10)多项式特征扩展器，将单项x扩展为多个x^i，然后传递到线性回归器
model = pl.make_pipeline(sp.PolynomialFeatures(10),
                         lm.LinearRegression())
model.fit(train_x, train_y)
pred_train_y = model.predict(train_x)
print(sm.r2_score(train_y, pred_train_y))
test_x = np.linspace(train_x.min(), train_x.max(),
                     1000).reshape(-1, 1)
pred_test_y = model.predict(test_x)
mp.figure('Polynomial Regression',
          facecolor='lightgray')
mp.title('Polynomial Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(train_x, train_y, c='dodgerblue',
           alpha=0.75, s=60, label='Sample')
mp.plot(test_x, pred_test_y, c='orangered',
        label='Regression')
mp.legend()
mp.show()