数学4如何用计算机画正切函数图像,7.3.4正切函数的性质和图像

教学课时：1课时

教学目标：

1.学生类比利用正弦线研究正弦函数性质的做法，探究利用正切线研究正切函数的性质；

2.学生能够利用正切函数的性质画出正切函数的图像，并结合图像进一步验证性质；

3.学生在探究的过程中，体会类比、换元、数形结合的数学思想，培养学生数学抽象、逻辑推理的学科素养.

教学重点：

(1)利用正切函数已有的知识(如定义、诱导公式、正切线等)研究性质.

(2)根据性质探究正切函数的图像.

教学难点：

画出正切函数的简图，体会与x轴的交点以及渐近线

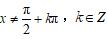，在确定图像形状时所起的关键作用.

教学过程：

一、提出问题，解决问题：

问题1：还记得研究正弦函数和余弦函数的方法吗？

【设计意图】共同回忆之前研究正余函数的方法，由性质得图像，体会以数辅形，以形助数的妙处，感受华罗庚的话：数形结合百般好！

问题2：正切函数是如何定义的？

【设计意图】教师辅以几何画板的演示，帮助学生回忆定义，特别是自变量的取值范围.

问题3：请画出各个象限角的正切线.

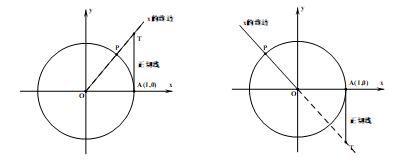
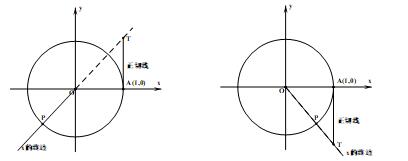
【设计意图】正切线可以直观地表示正切值，随着角的变化，为探究正切函数的性质做铺垫.

问题4：请你利用正切函数的定义，确定正切函数的定义域.

由正切函数的定义知：正切函数定义域为：

.

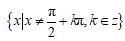【设计意图】研究函数优先考虑定义域，培养学生严谨的数学品质.其次，正切函数的定义域与正弦函数和余弦函数不同，给学生做着重强调.再次，学生不难得出定义域关于原点对称，为后面研究奇偶性做准备.

问题5：观察正切线的变化特点和规律，你能得出正切函数y=tanx具有哪些性质吗？

①定义域和值域：由正切线可以看出，正切函数的值域为全体实数.

②奇偶性：定义域是关于原点对称的，由诱导公式：且

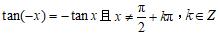，可知正切函数是奇函数(图像关于原点对称).

③周期性：由诱导公式：

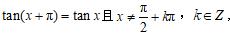,可知正切函数是周期函数，且周期为

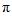(每隔

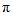个单位的函数图像是一样的).

④单调性：由单位圆中正切线的变化规律知：正切函数在区间

上，y值随x的增大而增大，是增函数，且角度无限接近

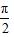，正切线向上无限延伸；角度无限接近

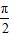，正切线向下无限延伸(图像是呈上升趋势.且没有尽头).

⑤ 零点：

.

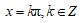【设计意图】引导学生主动思考，类比可以用正弦线研究正弦函数y=tanx性质的做法，用正切线研究正切函数的性质.正切函数的最小正周期为

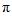，这一点与正弦函数、余弦函数也不同，特别需要引起学生的关注.学生能明确2

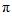是正切函数的周期，不一定能想到是正切函数的最小正周期，这一点可以将角多旋转几圈，多演示几次正切线的变化，由学生观察得出结论.

问题6：通过对正切函数性质的研究，你认为我们应该如何做出正切函数的图像？

【设计意图】引导学生明确，研究正切函数在一个周期内

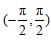的图像，由周期性就可以得到整个定义域内的图像，再由奇偶性，只要研究

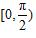的图像就可以.

问题7：如何做出正切函数在

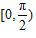上的图像？

课本56页列表描点连线(图7-3-16)

【设计意图】①需要注意的在区间

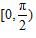上的特殊角的正切值非常少，特别是当x从

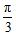继续增大时，正切值的变化情况要结合单调性加以分析，特别是当x逐渐逼近

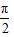的过程，正切值越来越大，逼近

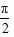意味着正切值趋近于

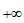，这就让学生认识到直线x=

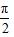是正切图像的一条渐近线.

②依据正切线能准确画出正切函数的图像，但不实用，在应用时一定要学会画简图(三点两

线法——

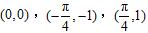和两条渐近线).

问题8：你能做出正切函数在定义域内的的图像吗？

【设计意图】再一次体会图像的特征，从图像的角度进一步验证函数的性质，培养学生利用函数图像研究函数性质的能力，加强“数形结合”的意识，并借此给出正切曲线的定义.

问题9：观察正切曲线思考：正切曲线是哪种对称图形，能试着说说？

正切函数y=tanx的图像是中心对称图形，其对称中心为

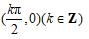
【设计意图】不难看出正切曲线是中心对称图形，学生容易发现的对称中心是

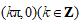，对于

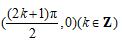也是图像的对称中心是不容易发现的，何况这些点也不在图像上.因此，正切曲线的对称性要放慢节奏.关于对称性这个结论可以给出证明：令f(x)=tanx，则

.

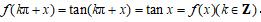问题10：观察正切曲线，判断下列命题的真假.

命题1：正切函数y=tanx是增函数；

命题2：正切函数y=tanx在其定义域上是增函数；

命题3：正切函数y=tanx在它的每一个周期内都是增函数；

命题4：正切函数y=tanx在每一个区间

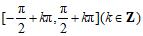上是增函数；

命题5：正切函数y=tanx在每一个区间

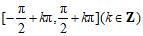上是增函数.

【设计意图】这是课本55页“想一想”的延伸，提出几个正切函数单调性的问题，让学生加以辨析，加深对性质的认识.

二、例题讲解，深化理解

例1(课本56页例1)求函数的

定义域.

思考：我们可以采用什么样的方法求出正切型函数的定义域呢？

解：令

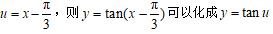
因为

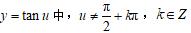,所以

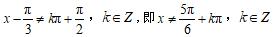
所以函数

.

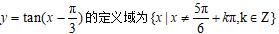【设计意图】本题属于正切型函数求定义域，在解答的过程中，教师要让学生体会换元的思想.由于正切函数的定义域是难点之一，例1要注意书写准确.

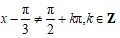是对的，但写成

的定义域为

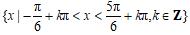是错误的，实际上，对于给定的常数k，自变量x只能取得一个周期的值，比如k=2时，这个集合只是

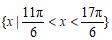，这与函数

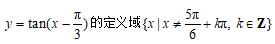完全不同.

变式训练：求函数

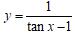的定义域.

解：由题意知

，

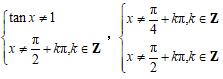解得：

.

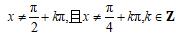所以函数

.

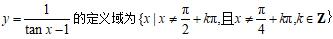【设计意图】tanx自身的限制往往被学生忽略，培养学生全面思考问题的能力.

例2(课本56页例2)求函数y=tan3x的周期.

思考：我们可以采用什么样的方法求出正切型函数的周期呢？

解：令u=3x，则y=tan3x可以化成y=tanu.

由y=tanu的周期为

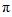可知，对任意u,当它增加到且至少要增加到u+

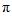时，对应的函数值才重复出现，因为

，

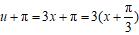这说明对任意x，当它增加到且至少要增加到

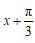时，y=tan3x的函数值才重复出现，

所以y=tan3x函数的周期为

.

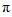【设计意图】本题属于正切型函数求周期，在解答的过程中，教师要让学生体会换元的思想.这是训练周期性的进一步深化，要继续规范地引导学生探寻思路、写好过程.

引申思考：(课本56页“想一想”)函数

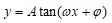(其中

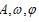都是常数，且

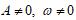)具有哪些性质？从定义域、值域、单调性、奇偶性、对称性等进行讨论.

【设计意图】引导学生归纳出形如函数

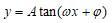(其中

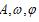都是常数，且

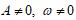)的性质，特别是周期公式

.

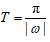三、课堂练习，巩固所学

1.(课本P56页练习A第1题)

求函数y=tan3x的定义域.

参考答案：

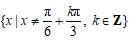
2.(课本P56页练习A第3题)

求下列函数的周期.

(1)

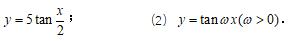
参考答案：

【设计意图】巩固正切函数的性质，学以致用.

四、归纳总结：

1.正切函数的性质有哪些？

2.正切曲线的画法有几种？

3.本节课涉及哪些数学思想、方法和学科核心素养.

【设计意图】带领学生从知识、方法和经验入手让学生自己先总结，同学们互相补充总结，加深理解.

五、布置作业

课本P56页练习A组2、4；B组2、4