Leetcode-85. Maximal Rectangle

公众号不定期发布一篇关于Leetcode解题技巧的文章，尝试从多角度、不同方法对题目进行解析。欢迎大家关注！

题目描述（困难难度）

给一个只有 0 和 1 的矩阵，输出一个最大的矩形的面积，这个矩形里边只含有 1。

解法一 暴力破解

参考这里，遍历每个点，求以这个点为矩阵右下角的所有矩阵面积。如下图的两个例子，橙色是当前遍历的点，然后虚线框圈出的矩阵是其中一个矩阵。

怎么找出这样的矩阵呢？如下图，如果我们知道了以这个点结尾的连续 1 的个数的话，问题就变得简单了。

1.首先求出高度是 1 的矩形面积，也就是它自身的数，如图中橙色的 4，面积就是 4。
2.然后向上扩展一行，高度增加一，选出当前列最小的数字，作为矩阵的宽，求出面积，对应上图的矩形框。
3.然后继续向上扩展，重复步骤 2。

按照上边的方法，遍历所有的点，求出所有的矩阵就可以了。

以橙色的点为右下角，高度为 1。

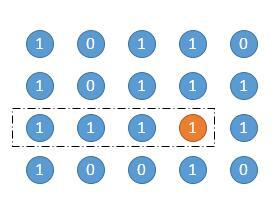
高度为 2。

高度为 3。

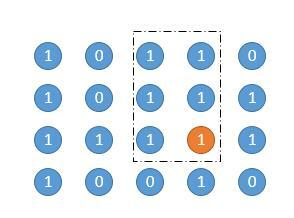
public class Maximal_Rectangle2 {
	
	public static int maximalRectangle(char[][] matrix) {
	    if (matrix.length == 0) {
	        return 0;
	    }
	    
	    //保存以当前数字结尾的连续 1 的个数
	    int[][] width = new int[matrix.length][matrix[0].length];
	    int maxArea = 0;
	    //遍历每一行
	    for (int row = 0; row < matrix.length; row++) {
	    	
	        for (int col = 0; col < matrix[0].length; col++) {
	     
	            //更新 width
	            if (matrix[row][col] == '1') {
	                if (col == 0) {
	                    width[row][col] = 1;
	                } else {
	                    width[row][col] = width[row][col - 1] + 1;
	                }
	            } else {
	                width[row][col] = 0;
	            }
	            
	            //记录所有行中最小的数
	            int minWidth = width[row][col];
	            //向上扩展行
	            for (int up_row = row; up_row >= 0; up_row--) {
	                int height = row - up_row + 1;
	                //找最小的数作为矩阵的宽
	                minWidth = Math.min(minWidth, width[up_row][col]);
	                //更新面积
	                maxArea = Math.max(maxArea, height * minWidth);
	            }
	            
	        }
	    }
	    return maxArea;
	}
	public static void main(String args[]) {
		char[][] matrix= {{'1','0','1','0','0'},{'1','0','1','1','1'},{'1','1','1','1','1'},{'1','0','0','1','0'}};
		int ans=maximalRectangle(matrix);
		System.out.println(ans);
	}
}

时间复杂度：O（m²n）。

空间复杂度：O（mn）。

解法二：使用柱状图 - 栈

是在 第84题解法二的的基础上进行改动。

import java.util.Stack;

public class Maximal_Rectangle3 {

	
	    public static int leetcode84(int[] heights) {
	        Stack < Integer > stack = new Stack < > ();
	        stack.push(-1);
	        int maxarea = 0;
	        for (int i = 0; i < heights.length; ++i) {
	            while (stack.peek() != -1 && heights[stack.peek()] >= heights[i])
	                maxarea = Math.max(maxarea, heights[stack.pop()] * (i - stack.peek() - 1));
	            stack.push(i);
	        }
	        while (stack.peek() != -1)
	            maxarea = Math.max(maxarea, heights[stack.pop()] * (heights.length - stack.peek() -1));
	        return maxarea;
	    }

	    public static int maximalRectangle(char[][] matrix) {

	        if (matrix.length == 0) return 0;
	        int maxarea = 0;
	        int[] dp = new int[matrix[0].length];

	        for(int i = 0; i < matrix.length; i++) {
	        	
	            for(int j = 0; j < matrix[0].length; j++) {
	                dp[j] = matrix[i][j] == '1' ? dp[j] + 1 : 0;
	            }
	            maxarea = Math.max(maxarea, leetcode84(dp));
	        } 
	        return maxarea;
	    }
	    public static void main(String args[]) {
			char[][] matrix= {{'1','0','1','0','0'},{'1','0','1','1','1'},{'1','1','1','1','1'},{'1','0','0','1','0'}};
			int ans=maximalRectangle(matrix);
			System.out.println(ans);
		}
}

时间复杂度 : O(NM)。对每一行运行 力扣 84 需要 M (每行长度) 时间，运行了 N 次，共计 O(NM)。

空间复杂度 : O(M)。我们声明了长度等于列数的数组，用于存储每一行的宽度。

解法三 动态规划

这是 leetcode Solution 中投票最高的，但比较难理解。

import java.util.Arrays;


public class Maximal_Rectangle4 {
	


    public static int maximalRectangle(char[][] matrix) {
        if(matrix.length == 0) return 0;
        
        int m = matrix.length;
        int n = matrix[0].length;

        int[] left = new int[n]; 
        int[] right = new int[n];
        int[] height = new int[n];

        Arrays.fill(right, n); // initialize right as the rightmost boundary possible

        int maxarea = 0;
        
        for(int i = 0; i < m; i++) {
            int cur_left = 0, cur_right = n;
            
            for(int j = 0; j < n; j++) {
                if(matrix[i][j] == '1') height[j]++;
                else height[j] = 0;
            }
            
            
            for(int j=0; j<n; j++) {
                if(matrix[i][j]=='1') 
                	left[j]=Math.max(left[j],cur_left);
                else {
                	left[j]=0; 
                	cur_left=j+1;
                	}
            }
            
            
            for(int j = n - 1; j >= 0; j--) {
                if(matrix[i][j] == '1') 
                	right[j] = Math.min(right[j], cur_right);
                else {
                	right[j] = n; 
                	cur_right = j;
                	}    
            }
            
            
            for(int j = 0; j < n; j++) {
                maxarea = Math.max(maxarea, (right[j] - left[j]) * height[j]);
            }
            
        }
        return maxarea;
    }
    public static void main(String args[]) {
			char[][] matrix= {{'1','0','1','0','0'},{'1','0','1','1','1'},{'1','1','1','1','1'},{'1','0','0','1','0'}};
			int ans=maximalRectangle(matrix);
			System.out.println(ans);
		}
}

时间复杂度 : O(NM)。每次对于N的迭代我们会对M迭代常数次。

空间复杂度 : O(M)， M 是我们保留的额外数组的长度。

总结

这道题还是很难的。即可以结合栈的知识点，又糅合了动态规划。在各大公司面试中，考的此处比较多，建议掌握动态规划和栈两种写法。

参考

1.解法一
2.解法二、解法三