编程题三角函数计算_极限—计算的技巧（第一章部分）

极限是高等数学上册中的一大难点，花样繁多的计算思路和强大的py能力让他能和任何一章毫无破绽的结合。

马上就要期末考试了，最近在复习的时候发现有很多的极限又不会算了，因此在这里总结记录一下我的学习心得，也希望能对你有所帮助。

(P.S.本来想一次整完，整着整着发现这是个天坑，所以就先把本章的知识整出来了，其他章的慢慢做吧。。）

一、有理函数的分式形式：

理论依据来自这个公式

直接考当然简单，但题目往往会变着花儿出题：

1）将无穷的符号删掉：

不管是什么题，如果求极限时出现无穷，直接倒代换就行了，不用想太多。只要考虑倒代换后的0的正负。

删掉符号后记得用绝对值处理！

（当然含有根号的函数也可以有理化处理，不再赘述。）

2）与数列结合：

与数列结合时，数列会默认n>0!!,因此极限一定存在！

（血的教训555）

3）在形式上下文章：

通常出现的形式为：

。遇到这种题，不要洛必达，直接“抓大放小”

二、两个重要极限和等价无穷小：

为什么要把这两样放在一块讨论呢？因为他们的条件都可以化为x趋近于零。

1）

其中标红的等价无穷小最重要！能大大简化你的计算！！

当然，考试的难点并不是直接应用，而是以函数的形式存在。

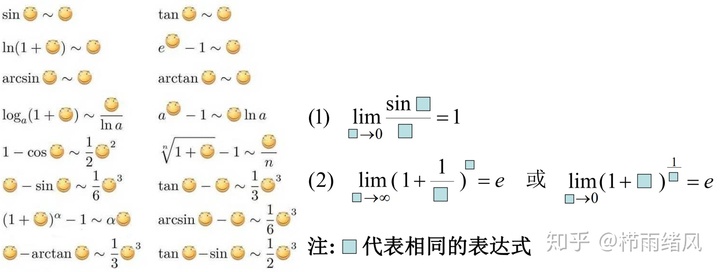
如图，只需让

趋于零即可带换。

下面的两道题就真的是硬凑出重要极限的形式，讲真，最近几年这种题老师超级爱出||__|/|

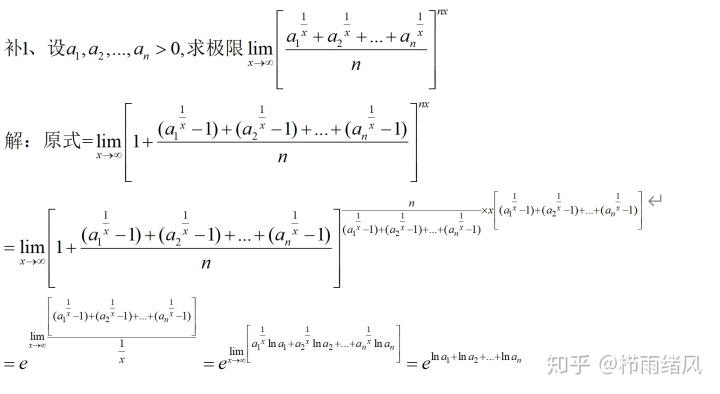
这道题主要是写起来太多了，容易抄错。

这道题的难点反而在于指数的计算（狗头微笑）

2）加减适用原则：

在等价无穷小的操作中，涉及到加减法一般不能用等价无穷小替换，如果分式中只有乘法除法，则可以使用等价无穷小替换。

因此，出现加减法算式时：

（1）转化为乘除法：

（2）整体性质的“1”的代换（比较难操作）

这位大佬讲的非常详细：

云山乱：高数常见坑点：等价无穷小​zhuanlan.zhihu.com

大佬yyds！！

这里再补充一下：如果是加减法：

1.整体进行“1”的乘法运算。

2.分别计算各部分极限是否存在

3.运用极限的减法法则计算结果

（3）同一分式型：

这种题讲究利用极限的四则运算处理（原因是各部分极限都存在且非0）

当然有混合型的题目，最为典型的是利用ln x的性质：

三、有界*无穷小型：

一句话：有界函数和无穷小的乘积仍是无穷小（0）。

这种题相对比较简单，但前提是你要能看出来。。。。。。

但是，看不出来就下饭……比如说下面的这道题：

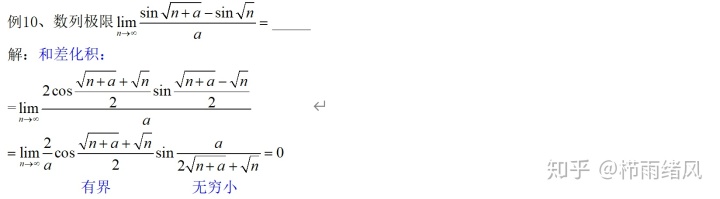
又是血的教训啊啊啊

四、提公因式型：

主要分为两大类：

补充：

也很常用！！！

这种题都要提出最高阶的无穷大，然后将剩下的部分进行等价无穷小变换。

这种题目中一般a=1,2,…也有e.

对于这种函数，一个易错点在于x趋近于极限时函数值的分类讨论:

0 或 无穷

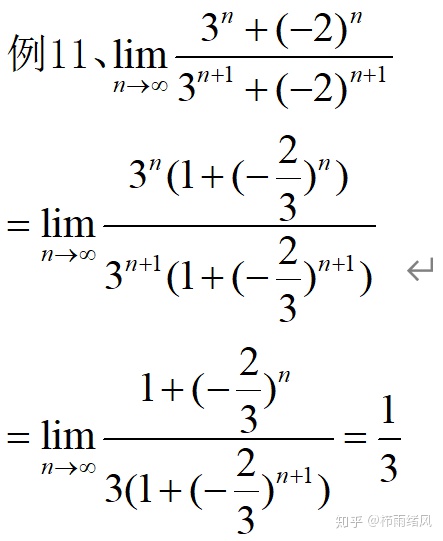
这道题是2和3，千万不要被吓到，提最高阶公因式之后直接算就行了。

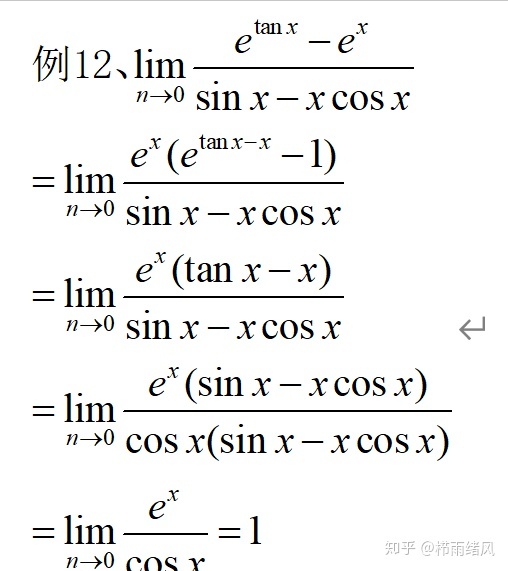
这道题主要在将e的x次方提取出来上存在问题，只要提取出来之后的操作就是等价无穷小了。

这两道题只要知道对x在趋于0时进行分类讨论，基本就没问题了。

提出a时可以考虑提出项再来一次等价无穷小。

在这种题中，容易出现的错误是没有看清楚自变量是谁。一般来说，在x的a次幂中，x为自变量，因此要讨论x的大小。

这种题换个角度看待，就是有理分式的问题。但是二者的不同之处在于趋近于极限时的变量不同。有理分式是x趋近于定值，较为简单；而这类题则是次数趋为定值4，需要讨论x的值，相对而言就麻烦了许多。

补充：在函数只含有一个三角函数相减的部分时，也要考虑提出tanx

五、三角函数趋于非零型：

纸老虎一个，用换元法，一换就出答案。

将其转换到趋近于0即可。

六、三角函数周期性：

在一部分只含有简单三角函数的极限中，需要利用三角函数周期性使函数“由易到难”再进行化简，其目的是提供可以操作的项。

在下面的题中，目的是处理根号项。