<think>好的,我现在需要回答用户关于单向空间后方交会程序设计的具体步骤。首先,我得先理解什么是空间后方交会。空间后方交会是通过已知的影像坐标和对应的地面控制点坐标,解算影像的外方位元素的过程。单向可能指的是单幅影像的处理,对吧?
接下来,我需要回忆相关的算法步骤。通常,空间后方交会需要用到共线方程,通过迭代方法解算外方位元素,比如线元素(Xs, Ys, Zs)和角元素(φ, ω, κ)。用户可能希望知道如何将这些数学原理转化为程序设计的步骤。
首先,程序需要输入数据,比如控制点的影像坐标和地面坐标,还有内方位元素如焦距f和像主点坐标(x0, y0)。然后初始化外方位元素,可能需要用近似值开始迭代。之后,构建误差方程,线性化共线方程,形成系数矩阵和常数项矩阵,解算改正数,更新外方位元素,直到满足收敛条件。
在编程实现时,需要注意矩阵运算,比如使用最小二乘法求解线性方程组。可能还需要处理数值计算的稳定性问题,比如矩阵求逆时的奇异情况。此外,迭代终止条件,如改正数的阈值或最大迭代次数,也需要设置。
用户提供的引用中提到了逐步集成和一次集成,这可能与程序设计的模块化有关,但不太确定是否直接相关。引用中的C语言例子可能对编程结构有参考,比如输入输出的处理,但空间后方交会更侧重于算法实现。
需要确保回答的结构清晰,分步骤说明,同时结合数学公式和编程要点。还要生成相关问题,可能涉及算法优化、误差分析或应用场景等。
现在需要组织语言,分步骤详细说明,并正确使用LaTeX格式。同时检查是否有遗漏的步骤,比如是否需要考虑畸变改正,或者是否需要引入权重矩阵。不过根据基础的空间后方交会,可能不需要这些高级内容,但可以简要提及可能的扩展。
最后,生成相关问题,帮助用户进一步学习,比如关于共线方程的推导、迭代方法的选择、程序调试技巧等。</think>### 单向空间后方交会程序设计步骤
单向空间后方交会是通过影像上已知的控制点像方坐标$(x,y)$和对应的物方坐标$(X,Y,Z)$,解算影像的外方位元素(线元素$X_S,Y_S,Z_S$和角元素$\phi,\omega,\kappa$)的过程[^1]。程序设计步骤如下:
---
#### **1. 数据输入与初始化**
- **输入参数**:
- 控制点的影像坐标$(x_i,y_i)$和地面坐标$(X_i,Y_i,Z_i)$,至少需要3个控制点
- 内方位元素(焦距$f$,像主点$(x_0,y_0)$)
- **初始化外方位元素**:
- 线元素$X_S^0,Y_S^0,Z_S^0$可通过粗略定位或近似值设定
- 角元素$\phi^0,\omega^0,\kappa^0$初始化为0或小角度值
---
#### **2. 构建共线方程**
利用共线条件方程建立误差方程:
$$
\begin{cases}
x_i - x_0 = -f \cdot \frac{a_1(X_i - X_S) + b_1(Y_i - Y_S) + c_1(Z_i - Z_S)}{a_3(X_i - X_S) + b_3(Y_i - Y_S) + c_3(Z_i - Z_S)} \\
y_i - y_0 = -f \cdot \frac{a_2(X_i - X_S) + b_2(Y_i - Y_S) + c_2(Z_i - Z_S)}{a_3(X_i - X_S) + b_3(Y_i - Y_S) + c_3(Z_i - Z_S)}
\end{cases}
$$
其中旋转矩阵$R$由$\phi,\omega,\kappa$通过方向余弦矩阵计算得到,例如$a_1 = \cos\phi\cos\kappa - \sin\phi\sin\omega\sin\kappa$[^2]。
---
#### **3. 线性化与迭代求解**
1. **线性化误差方程**:对共线方程进行泰勒展开,得到线性方程组
$$ V = A \cdot \Delta - L $$
其中$\Delta = [\Delta X_S, \Delta Y_S, \Delta Z_S, \Delta\phi, \Delta\omega, \Delta\kappa]^T$为外方位元素改正数,$A$为系数矩阵,$L$为常数项矩阵。
2. **最小二乘解算**:通过法方程$A^TA\Delta = A^TL$求解$\Delta$,更新外方位元素:
$$ X_S^{k+1} = X_S^k + \Delta X_S, \quad \phi^{k+1} = \phi^k + \Delta\phi \quad \text{等} $$
3. **收敛判断**:当改正数$\Delta$的绝对值小于阈值(如$10^{-6}$)或达到最大迭代次数时停止。
---
#### **4. 程序设计关键代码(伪代码)**
```python
def spatial_resection(control_points, f, x0, y0, max_iter=100, tol=1e-6):
Xs, Ys, Zs = initial_XYZ() # 初始化线元素
phi, omega, kappa = 0, 0, 0 # 初始化角元素
for _ in range(max_iter):
A = []
L = []
for (xi, yi), (Xi, Yi, Zi) in control_points:
R = compute_rotation_matrix(phi, omega, kappa) # 计算旋转矩阵
# 计算系数矩阵A和常数项L的具体元素(需展开泰勒级数)
# ...
A.append(row_coeffs)
L.append(residuals)
delta = np.linalg.lstsq(A, L, rcond=None)[0] # 最小二乘解算
# 更新外方位元素
Xs += delta[0]
Ys += delta[1]
Zs += delta[2]
phi += delta[3]
omega += delta[4]
kappa += delta[5]
if np.max(np.abs(delta)) < tol:
break
return Xs, Ys, Zs, phi, omega, kappa
```
---
#### **5. 注意事项**
- **控制点分布**:需均匀分布以提高解算精度
- **数值稳定性**:矩阵求逆时需避免奇异矩阵(可通过正则化处理)
- **扩展性**:可加入畸变改正模型(如径向畸变)提升精度
---
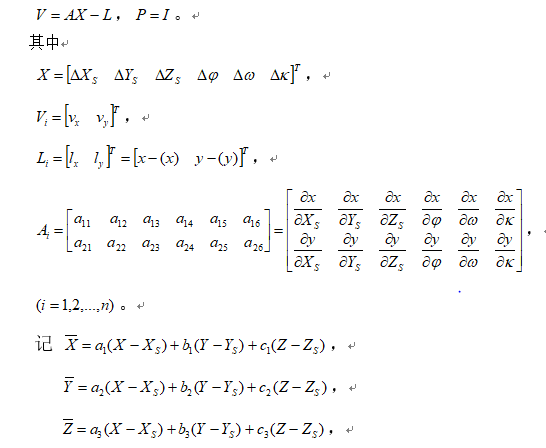








 本文介绍了空间后方交会的原理,通过C语言和Python实现。利用3个控制点的地面坐标和像坐标,解算影像的外方位元素。通过最小二乘法处理多余观测方程,提高解算精度。文中提供了一个Python代码示例,展示了如何计算外方位元素的过程。
本文介绍了空间后方交会的原理,通过C语言和Python实现。利用3个控制点的地面坐标和像坐标,解算影像的外方位元素。通过最小二乘法处理多余观测方程,提高解算精度。文中提供了一个Python代码示例,展示了如何计算外方位元素的过程。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 5905
5905

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








