单纯形法求最小值的检验数_线性规划的单纯形法总结

使用单纯形法求解下列规划问题：

线性

Max z = 2x1 + x2

5x2 <= 15

6x1 + 2x2 <= 24

x1 + x2 <= 5

x1, x2 >= 0

一、将上述问题化为标准型

其约束条件系数的增广矩阵为：

P3 、p4、p5是单位矩阵，构成一个基，对应变量x3 ， x4 ， x5是基变量，令非基变量x1，x2等于0，即找到一个初始基可行解：

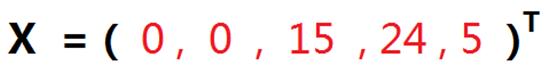
二、 单纯形表法

初始单存性表：

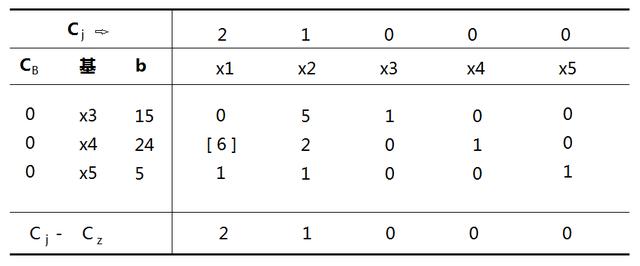
检验数2 = 2 – ( 0x 0 + 0 x6 + 0x 1 ) = 2

检验数1 = 1 – ( 0x 5 + 0 x5 + 0x 1 ) = 1

。。。

因为表中有大于0的检验数，所以表中的基可行解不是最优解，因为“检验数2>检验数1”，所以确定x1为换入变量。

将b列除以P1同行的数字得：

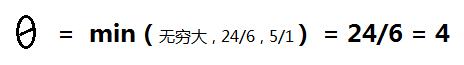
因为6为主元素，作为标志对6加上[ ] ，主元素所在行基变量x4为换出变量。用换入变量x1替换出变量x4，得到个新的基p3、p1、p5，将主元素变成1，该列其它元素变成0，经过线性变换，得到如下表：

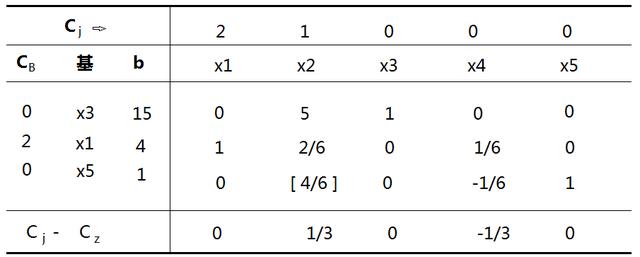
检验数2 = 2 – ( 0 x 0 + 2 x 1 + 0 x 0 ) = 0

检验数1 = 1 – ( 0 x 5 + 2 x 2/6 + 0 x 4/6 ) = 1/3

。。。

上述还存在检验数大于0 的数，反复迭代，得到下表：

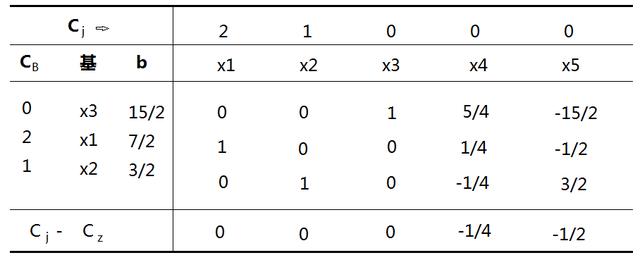
至此，所有检验数都<=0，得到最优解 X =(7/2, 3/2 , 15/2 , 0 , 0)，带入目标函数z = 2 x 7/2 + 3/2 = 17/2

《大数据和人工智能交流》的宗旨

1、将大数据和人工智能的专业数学：概率数理统计、线性代数、决策论、优化论、博弈论等数学模型变得通俗易懂。

2、将大数据和人工智能的专业涉及到的数据结构和算法：分类、聚类 、回归算法、概率等算法变得通俗易懂。

3、最新的高科技动态：数据采集方面的智能传感器技术；医疗大数据智能决策分析；物联网智慧城市等等。

根据初学者需要会有C语言、Java语言、Python语言、Scala函数式等目前主流计算机语言。

根据读者的需要有和人工智能相关的计算机科学与技术、电子技术、芯片技术等基础学科通俗易懂的文章。