无向图是欧拉图的充要条件_概率图模型(模型表示)

1.概率图模型是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型

2.贝叶斯网络是联合概率分布可分解为每个随机变量的局部条件概率的乘积形式的有向图模型

3.贝叶斯网络独立性体现在三种形式：head-to-head、tail-to-tail、head-to-tail

5.马尔可夫网络是满足任一随机变量在给定它邻居的情况下独立于所有其它变量的无向图模型

6.马尔可夫网络独立性体现在三个等价的关系：全局、局部和成对马尔科夫性

7.马尔可夫网络的联合概率分布可用吉布斯分布表示

8.贝叶斯网络又称有向图模型、信念网络

9.马尔可夫网络又称无向图模型、马尔可夫随机场

概率图模型(Probabilistic Graphical Model，PGM)，简称图模型，是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型。

我们从最基础的开始正式介绍概率图模型。为此，先补充一些预备知识。

预备知识

概率图模型的基础是概率，我们给出最重要的几条概率公式：

(1)—(3)在前面的文章反复提到，这里不再赘述。这里只给出链式法则的证明：

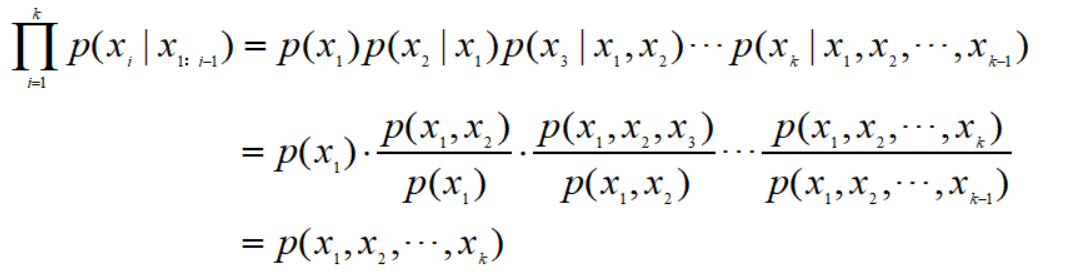
另外,我们介绍一下马尔科夫性。

定义1：马尔可夫性

如果p(X,Y|Z)=p(X|Z)p(Y|Z),则称事件X,Y对给定事件Z是条件独立的,称为马尔科夫性

场景引入

给定一组有K维随机变量的数据集，我们希望通过其联合概率分布学习其数据特征，也即对K维随机变量直接建模。假设每个变量都有m个取值，那么要学习的参数将会有m^k-1个，显然，这是指数级的难题，在实际中是不可接受的。

为此，我们需要做一些减少参数量的方法，一个有效的方法是独立性假设。将K维随机变量的联合分布分解为K个条件概率乘积(链式法则)：

如果某些变量之间存在条件独立，我们还能进一步大幅减少其参数量。

为了很好说明这一点，我们举一个例子。

假设对四个随机变量x1,x2,x3,x4求联合分布，它们并有如下关系：

• 已知x1条件下，x2和x3相互独立

• 已知x2、x3条件下，x1和x4相互独立

我们改写成数学语言，有：

根据第一个条件，结合条件概率公式，有：

于是可得到：

所以我们有：

根据第二个条件，我们有：

最后根据链式法则我们得到联合概率分布为：

可见，联合概率p(x)可分解为4个局部条件概率的乘积。如果每个维度都是二值变量，那么独立参数由15个(2^4-1)变为9个(1+2+2+4)

模型引出

当模型中的变量更多时，条件依赖关系更加复杂。我们考虑用图结构的方式来可视化这种关系，以一种直观、简单的方式描述随机变量之间的条件独立性的性质。比如上一节的四维随机变量，可以用如下结构表达：

定义2:概率图

图由一组节点和节点之间的边组成，在概率图模型中，每个节点都表示一个随机变或一组随机变量，边表示这些随机变量之间的概率依赖关系.

如果条件概率p(x2|x1)存在，那么用x1→x2表示。上图中表达了两个条件独立性

我们把x1称为x2、x3的父节点，而x4有两个父节点。

进一步，我们记变量xi的父节点集合为：

常见的概率图模型可以分为两类：有向图模型和无向图模型。有向图模型的图结构为有向非循环图，如果两个节点之间有连边，表示对于的两个变量为因果关系；无向图模型使用无向图来描述变量之间的关系，每条边代表两个变量之间有概率依赖关系.

贝叶斯网咯

有向图模型，也称贝叶斯网络(Bayesian Network)或信念网络(Belief Network)，是指用有向图来表示概率分布的图模型。

定义3:贝叶斯网络

对于一个随机向量X=[X1,X2,...,Xk]和有K个节点的有向非循环图G，G的每个节点代表一个随机变量，每条边(eij)表示两个随机变量Xi和Xj之间具备的非独立因果关系，若X的联合概率分布可以分解为每个随机变量Xk的局部条件概率的乘积形式，即：

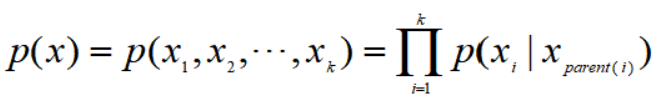
那么(G,X)构成一个贝叶斯网络.

对于贝叶斯网络，有两点需要强调，第一，这里的随机变量可以是可观测的变量，隐变量或者未知参数；第二是贝叶斯网络的性质——条件独立性。我们重点介绍。

条件独立性

在贝叶斯网络中，如果两个节点是直接连接的，它们肯定是非条件独立的直接因果关系，父节点是“因”，子节点是“果”。如果两个节点间接连接，那么分三种情况。

• tail-to-tail

根据链式法则和贝叶斯网络定义，有

于是我们得到共因关系

该结果表示，如果A被观测，则B与C独立，路径被阻塞。

• head-to-tail

同理我们有，

于是得到间接因果关系：

该结果表示，如果A被观测，则B与C独立，路径被阻塞。

• head-to-head

我们有

得到共果关系

该结果表示，默认情况下，B与C相互独立，路径被阻塞；若A被观测，B和C不独立，路径连通.

马尔可夫网络

无向图模型，也称为马尔可夫随机场(Markov Random Field,MRF)或马尔科夫网络(Markov Network)，是一类用无向图来描述一组具有局部马尔可夫性质的随机向量X的联合概率分布的模型。

定义4:马尔可夫网络

对于一个随机向量X=[X1,X2,...,Xk]和有K个节点的无向可循环图G，G的每个节点代表一个随机变量，每条边(eij)表示两个随机变量Xi和Xj的邻居关系，若其满足局部马尔可夫性质，即一个变量Xk在给定它邻居的情况下独立于所有其它变量：

其中N(k)为变量Xk的邻居集合，\k为除Xk外其它变量的集合，那么(G,X)就构成了一个马尔可夫随机场.

对于MRF，要关注的有两点，一个是其条件独立性的体现，一个是其联合概率分布的表示。

条件独立性

关于MRF，其条件独立性体现在三个方面：局部马尔可夫性、全局马尔可夫性和成对马尔可夫性。而且他们是相互等价的：

全局马尔可夫性(Global Markov Property)是指给定两个变量子集的分离集，则这两个变量子集条件独立.

这里先要介绍什么是分离集，

定义5:分离集(separating set)

若从结点集A中的结点到B中的结点都必须经过结点集C中的结点，则称结点集A和B被结点集C分离，C称为分离集.

比如下图：

集合A和集合B的任意一点要连接，必须经过集合C，C就是它们的分离集。

用数学表达全局马尔可夫性是，在无向图中给定三个集合ABC,如果满足给定XC的条件下，XA和XB相互独立，即

对应概率图表示为

局部马尔可夫性(Local Markov Property)是指给定某变量的邻接变量，则该变量条件独立于其他变量.

用数学表达是，变量Xk在给定它的邻居的情况下独立于所有其它变量：

比如下图：

局部马尔可夫表示为

成对马尔可夫性(Pairwise Markov Property)是指给定所有其他变量，两个非邻接变量条件独立.

用数学语言表达是，任意两个不是邻居关系的随机变量xi,xj，在给定其他所有随机变量下相互独立：

比如下图

那么其中一个成对马尔可夫性可表示为：

MRF联合分布

马尔可夫随机场的联合概率分布可以用因子分解来表示，先给结论。

因子分解：无向图的联合概率可以分解为一系列定义在最大团上的非负函数的乘积形式

为了说明这一点，先介绍两个概念。

定义6：最大团(MCP)

给定无向图G=(V,E)，其中V是非空集合，称为顶点集；E是V中元素构成的无序二元组的集合，称为边集，无向图中的边均是顶点的无序对，无序对常用圆括号“( )”表示。如果U∈V，且对任意两个顶点u，v∈U有(u,v)∈E，则称U是G的完全子图，G的完全子图是G的团。如果一个团不被其他任一团所包含，则称该团为图G的极大团，最大团就是结点数最多的极大团

举个例子，对于下面的无向图：

所有的极大团为：

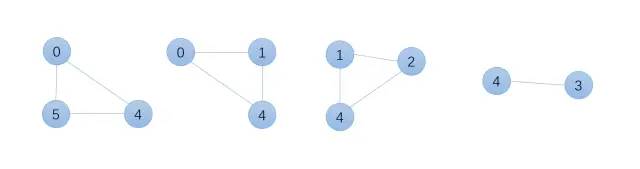
注：1和5没边直接相连，不满足定义；同理1和3也无相连

最大团为：

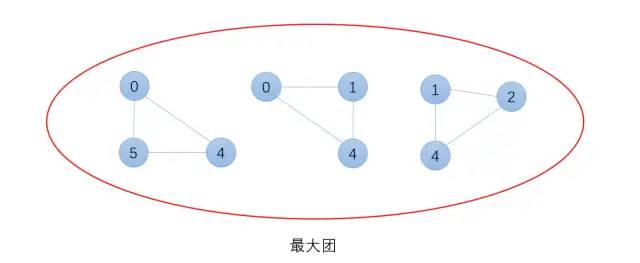
定义7：吉布斯分布

在无向图模型G上的一个概率分布称之为吉布斯分布，如果它能够因子分解为定义在最大团上的正函数的乘积，最大团覆盖G的所有顶点和边。即

观察一下吉布斯分布的表达式，它与指数族分布形式相同，因此，满足最大熵原理。

注：最大熵原理的指数族分布在之前文章有详细介绍从【为什么要用sigmoid函数】到真的懂【逻辑回归】

那么这个跟MRF有什么关系呢，天才数学家证明了一个定理：Hammersley Clifford定理，该定理得到如下结论：

也就是说，马尔可夫随机场(MRF)的联合概率分布可以用吉布斯分布表示。

最后，化简一下吉布斯分布：

该形式的分布又称为玻尔兹曼分布(Boltzmann Distribution)。任何一个无向图模型都可以用上式来表示其联合概率

参考资料

https://zhuanlan.zhihu.com/p/113218415

https://www.jianshu.com/p/dabbc78471d7

https://www.cnblogs.com/iamxyq/p/5949609.html