c# 傅里叶变换 频域_傅里叶在时域与频域的变换及应用！

---

Fourier transform或Transformée de Fourier有多个中文译名，常见的有“傅里叶变换”、“付立叶变换”、“傅立叶转换”、“傅氏转换”、“傅氏变换”、等等。

傅立叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，傅立叶变换用正弦波作为信号的成分。

从前在时域和频域的边界上，有一颗高高的树叫作高数，上面长满了傅里叶。

在书中，关于傅里叶变换的介绍非常多，其核心公式为：

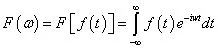
那么问题来了，这个公式和我们信号完整性有什么关系呢？

也许很多同学在毕业后就已经将这些知识悉数还给了任课老师，所以我们从信号完整性的角度，尽可能简单的回顾一下傅里叶变换的应用。

在应用傅里叶变换之前，我们需要先了解时域与频域。

时域是描述时间顺序上先后发生的事情。比如，我们仿真得到的波形，看到的眼图，这些都是时域的信号。有时间、电压，以时间为坐标轴，表示动态的信号关系就是时域。

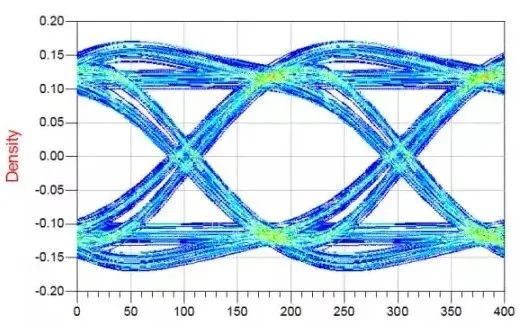
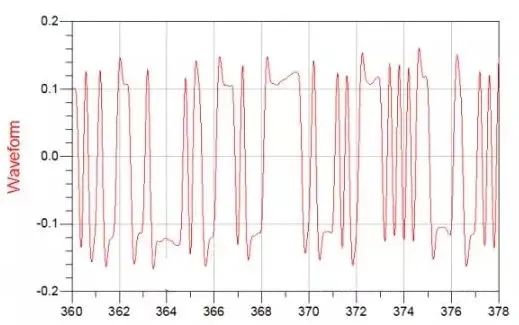
上图的这个波形比较复杂，我们先看一个最简单的波形，这是一个标准的正弦波：

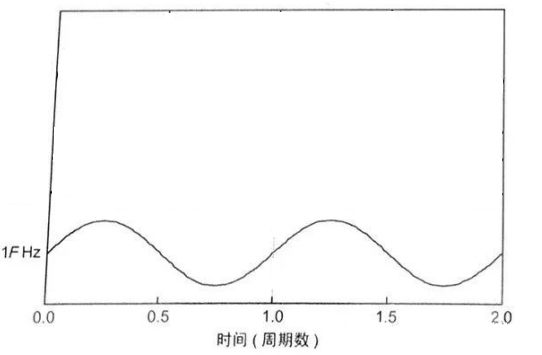
在这个波形的基础上，我们还可以画出它三倍频的波形、五倍频的波形、七倍频的波形……

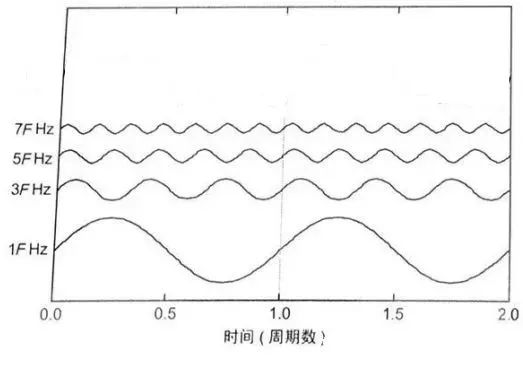
将所有的波形叠加到一起，该加的地方加，该减的地方减，最终我们就能得到叠加后的波形：

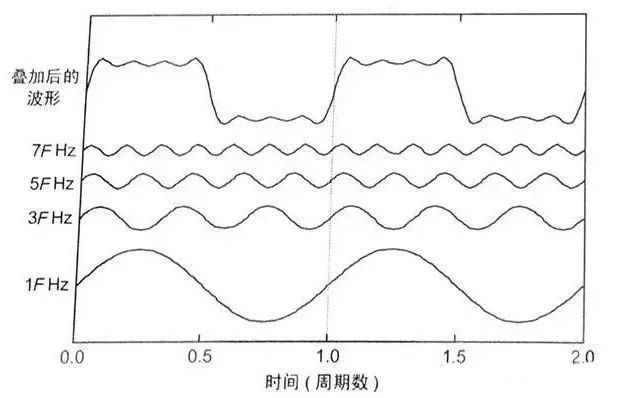
叠加后的波形相较于基频或是谐波，上升沿变得更加陡峭，这也是我们在分析信号时最常见的波形形式。也就是说我们所看见的波形，并不是一个单一的波形，而是各个频率波形叠加后的效果。叠加的高频谐波越多，波形的上升沿就越陡峭。理论上只要叠加的高频谐波足够多，就能够形成方波(实际上不行，存在吉布斯效应)。

波形的原理已经清楚了，但是我们将一个波形根据频率拆分为无数个波形还是太过于抽象，这种情况就需要傅里叶变换上场了。

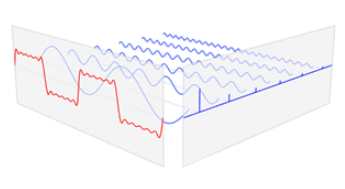
在上面这张图中，红色部分是基波和多个谐波叠加后的波形，是时域的表现形式。右侧将波形的幅度量化，使其表现在不同的频率上，这就是时域。

将上图的时域波形做一些改变，把谐波的分布频率作为X 轴，幅度为Y 轴，我们就可以得到波形的能量分布，如下图：

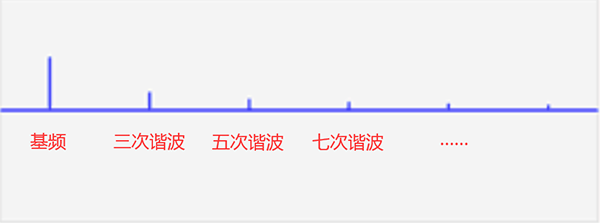
这就是频域。

频域虽然没有时域直观，但是频域能够得到很多时域无法明确表达的信息，S 参数就是频域的一种，至于S 参数有多方便，大家也就都知道了。

时域与频域的转换并不需要大家手动去计算，卷积算法(快速傅里叶)几乎每一个仿真软件都在应用，非常方便就可以将时域与频域互相转换。

总结一下，我们所看到的波形都可以分解为无数个不同频率的叠加，高频谐波叠加的越多，边沿越陡峭。反过来，边沿陡峭的信号一定有更多的高频分量，因此我们评估信号的带宽并不是依靠信号的频率，而是根据信号的边沿时间来求解带宽频率。

最后，纪念一下这一切的由来。法兰西的荣光、欧塞尔人的骄傲、远征埃及的指挥官、格伦诺布尔的决策者、科学院院士暨理工科大学校务委员会主席、时域与频域的贯通者、伟大的变换大师：让·巴普蒂斯·约瑟夫·傅里叶男爵。

傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。

【免责声明】本文来自PCB设计与信号完整性仿真(ID：Fourteen-SI)及声振之家，版权归原作者所有，仅用于学习等，对文中观点判断均保持中立，若您认为文中来源标注与事实不符，若有涉及版权等请告知，将及时修订删除，谢谢大家的关注！