时间序列分析实验报告总结_时间序列分析

一.时间序列

时间序列分析​mp.weixin.qq.com

1.定义

某些量在时间上的变化，自变量为时间。

如：股票数据，客流数据，天气数据，日志数据

2.分类

• 根据研究对象的多少，可以分为一元与二元
• 根据时间是否具有连续性，可以分为离散型与连续型的时间序列
• 根据时间序列的统计特性，可以分为平稳时间序列与非平稳的时间序列

3.时间序列的分析方法

（1）随机性时间序列分析

• 自回归模型（AR）
• 滑动平均模型（MA)
• 自回归滑动平均模型（ARMA）
• 差分自回归滑动平均模型（ARIMA）

（2）确定性时间序列分析

• 趋势预测法
• 平滑预测法
• 分解分析法

4.时间序列的影响因素

• 长期趋势（Trend)
• 循环变动、周期性（cycle）
• 季节性变化（seasonal variation)
• 不规则变化（irregular movement)

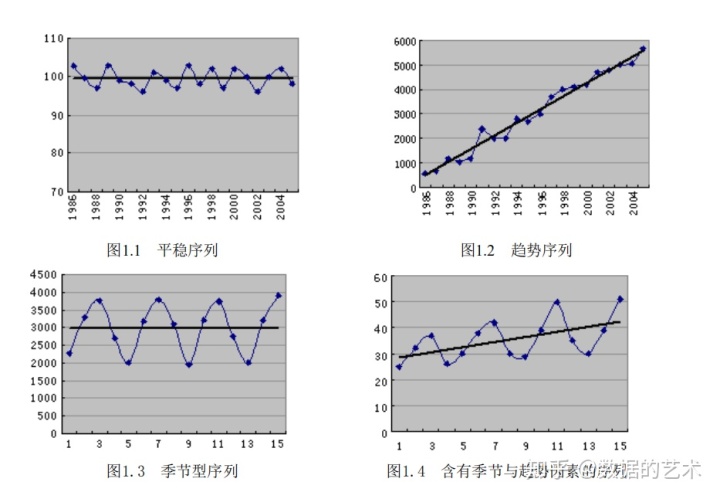
5.时间序列的分析模型

加法模型：Y=T+S+C+I

乘法模型：Y=T*S*C*I

二.时间序列分析

1.时间序列的数学定义

随机变量{Yt:t=1,2,3.....}称为一个时间序列模型

均值函数:μ=E(Yt)

2.平稳性

若时间序列{Yt:t=0,1,2,3......}的每一个数值都是从一个概率分布中随机得到，如果满足

• 均值E（Yt）=μ是与时间t无关的常数
• 方差VAR（Yt)=γ是与时间t无关的常数
• 协方差是只与时期间隔k有关，与时间t无关的常数

则我们认为改时间序列是平稳的（stationary)

三.随机性时间序列分析

1.分析过程

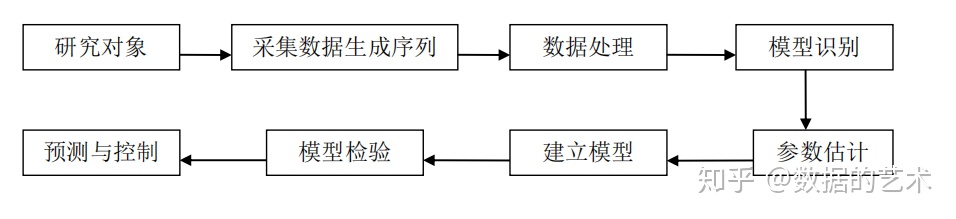
• 用观测、调查、统计、抽样等方法取得被观测系统时间序列动态数据。
• 根据动态数据作相关图，进行相关分析，求自相关函数。相关图能显示出变化的趋势和周期，并能发现跳点和拐点。跳点是指与其他数据不一致的观测值。如果跳点是正确的观测值,在建模时应考虑进去，如果是反常现象，则应把跳点调整到期望值。拐点则是指时间序列从上升趋势突然变为下降趋势的点。如果存在拐点，则在建模时必须用不同的模型去分段拟合该时间序列，例如采用门限回归模型。
• 辨识合适的随机模型，进行曲线拟合，即用通用随机模型去拟合时间序列的观测数据。对于短的或简单的时间序列，可用趋势模型和季节模型加上误差来进行拟合。对于平稳时间序列，可用通用ARMA模型（自回归滑动平均模型）及其特殊情况的自回归模型、滑动平均模型或组合-ARMA模型等来进行拟合。当观测值多于50个时一般都采用ARMA模型。对于非平稳时间序列则要先将观测到的时间序列进行差分运算，化为平稳时间序列，再用适当模型去拟合这个差分序列。

指仅用它的过去值及随机扰动项所建立起来的模型，其一般形式为

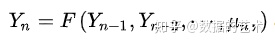
取线性方程、一期滞后以及白噪声随机扰动项

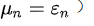
2.ＡＲ模型

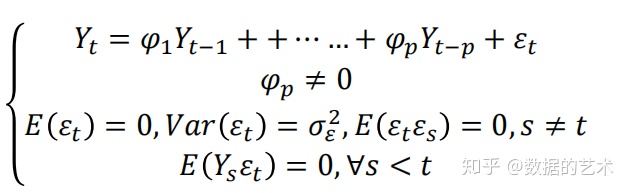
该模型为P阶自回归模型

3.滑动平均模型

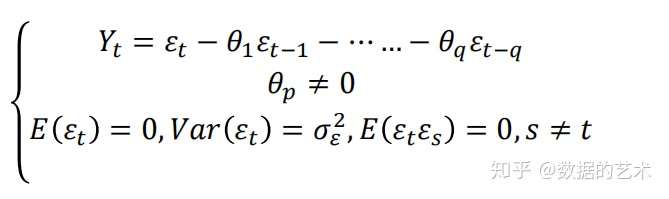
该模型为q阶滑动平均模型

4.自回归滑动平均模型

• 一个随机时间序列可以通过一个自回归移动平均过程生成，即该序列可以由其自身的过去或滞后值以及随机扰动项来解释。
• 如果该序列是平稳的，即它的行为并不会随着时间的推移而变化，那么我们就可以通过该序列过去的行为来预测未来。这也正是随机时间序列分析模型的优势所在。需要说明的是，上述ARMA(p，q)模型中均未包含常数项。如果包含常数项，常数项并不影响模型的原有性质，因为通过适当的变形，将包含常数项的模型转换为不含常数项的模型

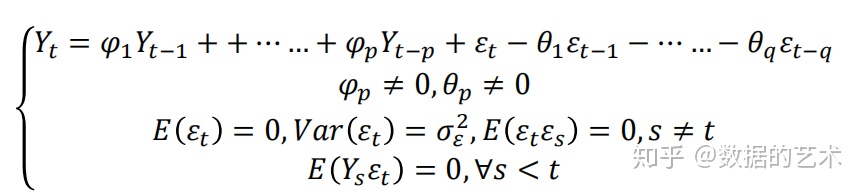
四.非随机性时间序列模型

1.随机性时间序列分析

(1)差分自回归滑动平均模型(p,d,q)

p:自回归阶数

d:差分阶数

q:移动平均阶数

原理:通过差分运算将非平稳时间序列模型转化为平稳时间序列模型

• 差分

(2)确定性时间序列分析

平滑法:去除序列中的短期效应

• 简单移动平均
• 即把若干历史时期的统计数值作为观察值，求出算术平均数作为下期预测值。这种方法基于下列假设：“过去这样，今后也将这样”，把近期和远期数据等同化和平均化，因此只能适用于事物变化不大的趋势预测。如果事物呈现某种上升或下降的趋势，就不宜采用此法。

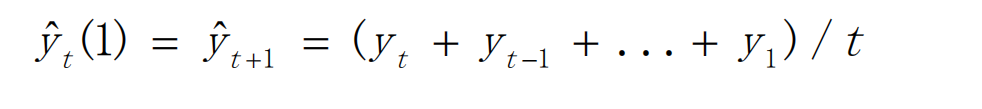
• 加权移动平均:对不同时间点的数据赋予不同的权重
• 把各个时期的历史数据按近期和远期影响程度进行加权，求出平均值，作为下期预测值

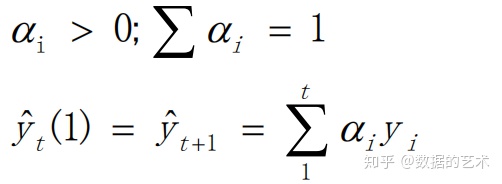
• k期移动平均:选择k个时间期数来预测

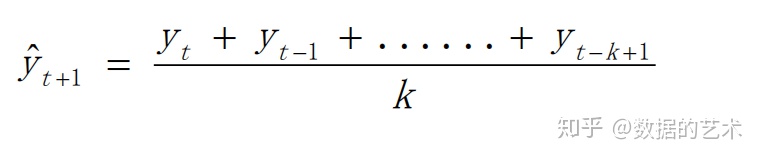
平滑法

指数平滑法

• 一次指数平滑法:适用于时间数列无明显的变化趋势

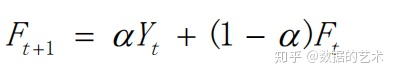
• 二次指数平滑法:对一次指数平滑的再平滑,适用于具有线性趋势的时间序列.
• 平滑会增加自相关,自相关数据不再适用于线性回归模型

五.趋势拟合法

1.线性趋势预测模型:利用最小二乘法估计参数,最后利用线性回归的思想求解

2.非线性趋势预测模型

转换为线性模型求解参数