地球的投影

                 因为要在bingmap中求n个地理坐标的面积的问题，涉及到一些地理信息方面的知识，因为对这方面的知识了解甚少。所以把一些知识整理下，供以后查看。今天先说一下地球的投影方面的问题。

（一）概念：

地球的投影：把地球上的点和线投影到可展的曲面(平面、园柱面或圆锥面)上，将此可展曲面展成平面，建立该平面上的点、线和地球椭球面上的点、线的对应关系。

（二）常用的椭球参数系数:

（1）954年北京坐标系（北京54）：
    a．属参心大地坐标系，参考椭球面与苏联及我国东北等地大地水准面（Datum）符合较好，54坐标系统普遍低于我国的大地水准面，平均误

差为29米左右；
    b．采用1940克拉索夫斯基Krassovsky椭球的两个几何参数：a=6378245m b=6356863.018773m  α=0.33523298692 
    c．大地原点在原苏联的普尔科沃（Pulkovo 1942）；
    d．采用多点定位法进行椭球定位；
    e．高程基准为 1956年青岛验潮站求出的黄海平均海水面；
    f．高程异常以原苏联 1955年大地水准面重新平差结果为起算数据。按我国天文水准路线推算而得。

（2）1980年西安坐标系（西安80）：
    a．属参心大地坐标系，参考椭球面与我国大部分地区大地水准面符合较好；
    b．1975年IUGG/IAG第16届大会推荐的地球椭球参数：a=6378140m b=6356755.2881575m，α=0.0033528131778

   c．国家大地原点设在陕西省泾阳县；
    d．采用多点定位法进行椭球定位；
    e．高程基准为 1956年青岛验潮站求出的黄海平均海水面；
    f．高程异常以原苏联 1955年大地水准面重新平差结果为起算数据。按我国天文水准路线推算而得。

（3）1984年WGS-84（WGS-84）：
    a．属地心坐标系，即以地心作为椭球体中心；
    b．WGS-84地球椭球参数：a=6378137m b=6356752.3142451m，α=0.00335281006247 

(三)投影的分类：

（1）变形性质分类：等角投影、等面积投影、等距投影

          等角投影  (Conformal mapping):  地物形状保持不变以外，在地图上测量两个地物之间的角度也能和实地保持一致，但高纬度地区地物的面积会被放大 。 常用于航海图、风向图、洋流图等
          等面积投影(Equivalent mapping)：显示出来的地物相对面积比例准确，但是形状会有变化。绘制经济地区图和某些自然地图。对于大多数数学地图和小比例尺普通地图来说，应优先考虑等积的要求。
          等距投影：在非等角等面积投影（这类投影既不等角也不等积，长度、角度、面积都有变形）其中有些投影在某个主方向上保持长度比例等于1。任意投影常用作数学地图，以及要求沿某一主方向保持距离正确的地图。

          补充说明：常用作世界地图的投影有墨卡托投影（Mercator）、高尔投影、摩尔威特投影、等差分纬线多圆锥投影、格灵顿投影、桑森投影、乌尔马耶夫投影等。
                      墨卡托投影适：用于海图，其面积变形随着纬度的增高而加大，但其方向变形很小
                      横轴墨卡托投影：投影的面积变形随着距中央经线的距离的加大而增大，适用于国家地图！
                      高斯－克吕格投影（Gauss_Krivger）属于等角横切椭圆柱投影，是设想用一个椭圆柱横套在地球椭球的外面，并与设定的中央经线相切。其经纬线互相垂直，变形最大位于  赤道与投影带最外一条经线的交点上，常用于纬度较高地区。
（2）构成成分分类：
     1。几何投影：方位投影、圆柱投影、圆锥投影

     

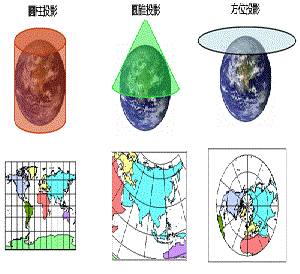
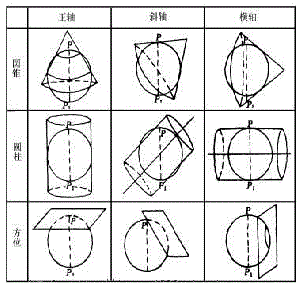
     2。非几何投影：伪方位投影、伪圆柱投影、伪圆锥投影、多圆锥投影

（四）常见投影简介：

（1）墨卡托(Mercator)投影
       墨卡托(Mercator)投影，是一种"等角正切圆柱投影”，荷兰地图学家墨卡托（Gerhardus Mercator 1512－1594）在1569年拟定, 假设地球被围在一中空的圆柱里，其标准纬线与圆柱相切接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。 墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。墨卡托投影的地图上长度和面积变形明显，但标准纬线无变形，从标准纬线向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。海底地形图编绘规范”（GB/T 17834-1999，海军航保部起草）中规定1：25万及更小比例尺的海图采用墨卡托投影，其中基本比例尺海底地形图（1：5万，1：25万，1： 100万）采用统一基准纬线30°，非基本比例尺图以制图区域中纬为基准纬线。基准纬线取至整度或整分。
       墨卡托投影坐标系：取零子午线或自定义原点经线(L0)与赤道交点的投影为原点，零子午线或自定义原点经线的投影为纵坐标X轴，赤道的投影为横坐标Y轴，构成墨卡托平面直角坐标系。
       高斯-克吕格(Gauss-Kruger)投影与UTM投影（Universal Transverse Mercator，通用横轴墨卡托投影）都是横轴墨卡托投影的变种，目前一些国外的软件或国外进口仪器的配套软件往往不支持高斯-克吕格投影，但支持 UTM投影，因此常有把UTM投影当作高斯-克吕格投影的现象。从投影几何方式看，高斯-克吕格投影是“等角横切圆柱投影( transverse conformal cylinder projection)”，投影后中央经线保持长度不变，即比例系数为1；UTM投影是“等角横轴割圆柱投影”，圆柱割地球于南纬80度、北纬84度两条等高圈，投影后两条割线上没有变形，中央经线上长度比0.9996。从计算结果看，两者主要差别在比例因子上，高斯-克吕格投影中央经线上的比例系数为1， UTM投影为0.9996，高斯-克吕格投影与UTM投影可近似采用 X[UTM]=0.9996 * X[高斯]，Y[UTM]=0.9996 * Y[高斯]，进行坐标转换（注意：如坐标纵轴西移了500000米，转换时必须将Y值减去500000乘上比例因子后再加500000）。从分带方式看，两者的分带起点不同，高斯-克吕格投影自0度子午线起每隔经差6度自西向东分带，第1带的中央经度为3°；UTM投影自西经180°起每隔经差6度自西向东分带，第1带的中央经度为-177°，因此高斯-克吕格投影的第1带是UTM的第31带。此外，两投影的东伪偏移都是500公里，高斯-克吕格投影北伪偏移为零，UTM北半球投影北伪偏移为零，南半球则为10000公里。
（2）高斯-克吕格投影简介
       高斯-克吕格(Gauss-Kruger)投影，是一种“等角横切圆柱投影”。德国数学家、物理学家、天文学家高斯（Carl Friedrich Gauss，1777一 1855）于十九世纪二十年代拟定，后经德国大地测量学家克吕格（Johannes Kruger，1857～1928）于 1912年对投影公式加以补充，故名。设想用一个圆柱横切于球面上投影带的中央经线，按照投影带中央经线投影为直线且长度不变和赤道投影为直线的条件，将中央经线两侧一定经差范围内的球面正形投影于圆柱面。然后将圆柱面沿过南北极的母线剪开展平，即获高斯一克吕格投影平面。高斯一克吕格投影后，除中央经线和赤道为直线外，其他经线均为对称于中央经线的曲线。高斯-克吕格投影没有角度变形，在长度和面积上变形也很小，中央经线无变形，自中央经线向投影带边缘，变形逐渐增加，变形最大处在投影带内赤道的两端。由于其投影精度高，变形小，而且计算简便（各投影带坐标一致，只要算出一个带的数据，其他各带都能应用），因此在大比例尺地形图中应用，可以满足军事上各种需要，并能在图上进行精确的量测计算。按一定经差将地球椭球面划分成若干投影带,这是高斯投影中限制长度变形的最有效方法。分带时既要控制长度变形使其不大于测图误差，又要使带数不致过多以减少换带计算工作，据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。通常按经差6度或3度分为六度带或三度带。六度带自 0度子午线起每隔经差6度自西向东分带，带号依次编为第 1、2…60带。三度带是在六度带的基础上分成的，它的中央子午线与六度带的中央子午线和分带子午线重合，即自 1.5度子午线起每隔经差3度自西向东分带，带号依次编为三度带第 1、2…120带。我国的经度范围西起 73°东至135°，可分成六度带十一个，各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°，或三度带二十二个。我国大于等于50万的大中比例尺地形图多采用六度带高斯-克吕格投影，三度带高斯-克吕格投影多用于大比例尺测图，如城建坐标多采用三度带的高斯-克吕格投影。
（3）UTM投影简介
       UTM投影全称为“通用横轴墨卡托投影”，是一种“等角横轴割圆柱投影”，椭圆柱割地球于南纬80度、北纬84度两条等高圈，投影后两条相割的经线上没有变形，而中央经线上长度比0.9996。UTM投影是为了全球战争需要创建的，美国于1948年完成这种通用投影系统的计算。与高斯-克吕格投影相似，该投影角度没有变形，中央经线为直线，且为投影的对称轴，中央经线的比例因子取0.9996是为了保证离中央经线左右约330km处有两条不失真的标准经线。UTM投影分带方法与高斯-克吕格投影相似，是自西经180°起每隔经差6度自西向东分带，将地球划分为60个投影带。我国的卫星影像资料常采用UTM投影。高斯-克吕格投影与UTM投影坐标系高斯- 克吕格投影与UTM投影是按分带方法各自进行投影，故各带坐标成独立系统。以中央经线（L0）投影为纵轴X, 赤道投影为横轴Y，两轴交点即为各带的坐标原点。为了避免横坐标出现负值，高斯- 克吕格投影与UTM北半球投影中规定将坐标纵轴西移500公里当作起始轴，而UTM南半球投影除了将纵轴西移500公里外，横轴南移10000公里。由于高斯-克吕格投影与UTM投影每一个投影带的坐标都是对本带坐标原点的相对值，所以各带的坐标完全相同，为了区别某一坐标系统属于哪一带，通常在横轴坐标前加上带号，如(4231898m,21655933m)，其中21即为带号。