余弦相似度

最新推荐文章于 2025-08-23 20:28:56 发布

weixin_34414650

最新推荐文章于 2025-08-23 20:28:56 发布

阅读量122

点赞数

文章标签： python

本文深入探讨了余弦相似度的概念，通过实例展示了如何计算两个向量的相似度，并提供了Python代码实现，帮助读者更好地理解向量在高维空间中的位置关系。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

转载自：http://www.ruanyifeng.com/blog/2013/03/cosine_similarity.html
评：作者写的通俗易懂。实在不需要改进了，一下仅仅是加深个人印象，便于个人记忆。

第一步：分词

句子A：我/喜欢/看/电视，不/喜欢/看/电影。
句子B：我/不/喜欢/看/电视，也/不/喜欢/看/电影。

第二步：列出所有词

我，喜欢，看，电视，电影，不，也。

第三步：计算词频

句子A：我 1，喜欢 2，看 2，电视 1，电影 1，不 1，也 0。
句子B：我 1，喜欢 2，看 2，电视 1，电影 1，不 2，也 1。

第四步：写出词频向量

句子A：[1, 2, 2, 1, 1, 1, 0]
句子B：[1, 2, 2, 1, 1, 2, 1]

问题转化为，计算向量相似度：

高维向量的空间解释：都是从[0, 0, 0, 0, ...]出发，指向不同方向

0度，完全重合
90度，完全不相似
180度，完全相反
理论：通过夹角的大小来判断向量的相似度，夹角越小就越相似

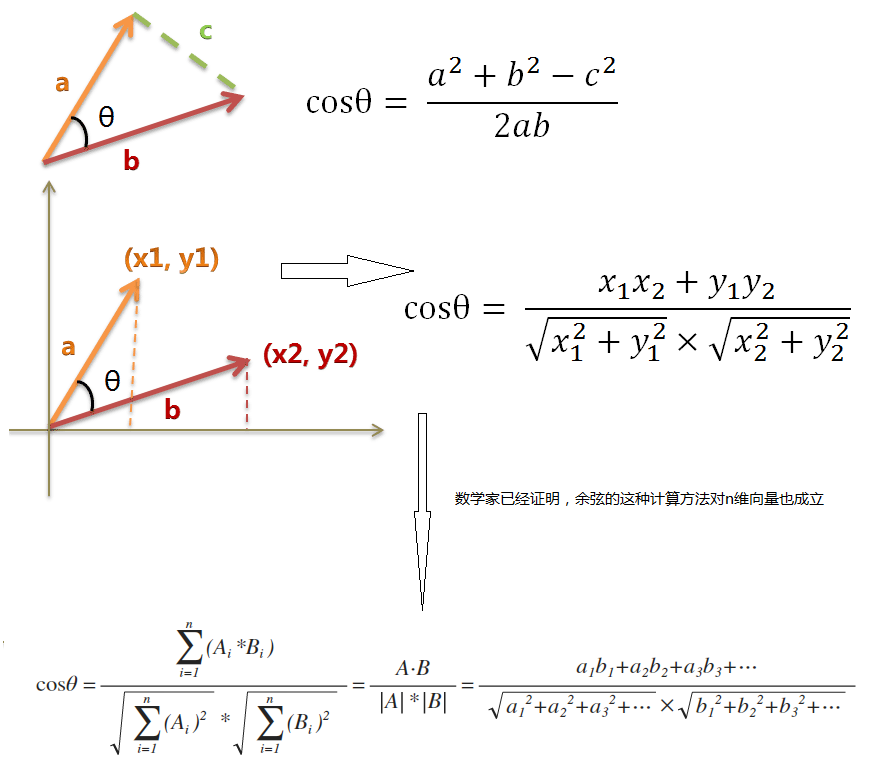
附：python计算余弦相似度

__author__ = 'dell'

import math

a = [1, 2, 2, 1, 1, 1, 0]
b = [1, 2, 2, 1, 1, 2, 1]

dot = [0 for i in range(len(a))]

for i in range(len(a)):
    dot[i] = a[i] * b[i]

n = sum(dot)

sum_a = math.sqrt(sum([i ** 2 for i in a]))
sum_b = math.sqrt(sum([i ** 2 for i in b]))

res = n / (sum_a * sum_b)

print res


def SimCosine(a, b):
    dot = [0 for i in range(len(a))]
    for i in range(len(a)):
        dot[i] = a[i] * b[i]
    sum_a = math.sqrt(sum([i ** 2 for i in a]))
    sum_b = math.sqrt(sum([i ** 2 for i in b]))
    res = sum(dot) / (sum_a * sum_b)
    return res


res = SimCosine(a, b)

print res

运行的结果：
C:\Python27\python.exe F:/Statis/Cosine.py
0.938194187433
0.938194187433