归并排序

最新推荐文章于 2025-08-18 22:47:43 发布

weixin_34408717

最新推荐文章于 2025-08-18 22:47:43 发布

阅读量43

点赞数

CC 4.0 BY-SA版权

文章标签： java

原文链接：http://www.cnblogs.com/zhanghaodong/p/10337824.html

本文深入讲解了归并排序的原理，采用分治策略通过递归实现。提供了详细的Java代码示例，包括排序和合并两个有序数组的过程。分析了归并排序的时间复杂度为O(n*logN)，空间复杂度为O(n)，确认其为稳定但非原地排序。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

归并排序原理：

利用分治的思想，通过递归来实现的，

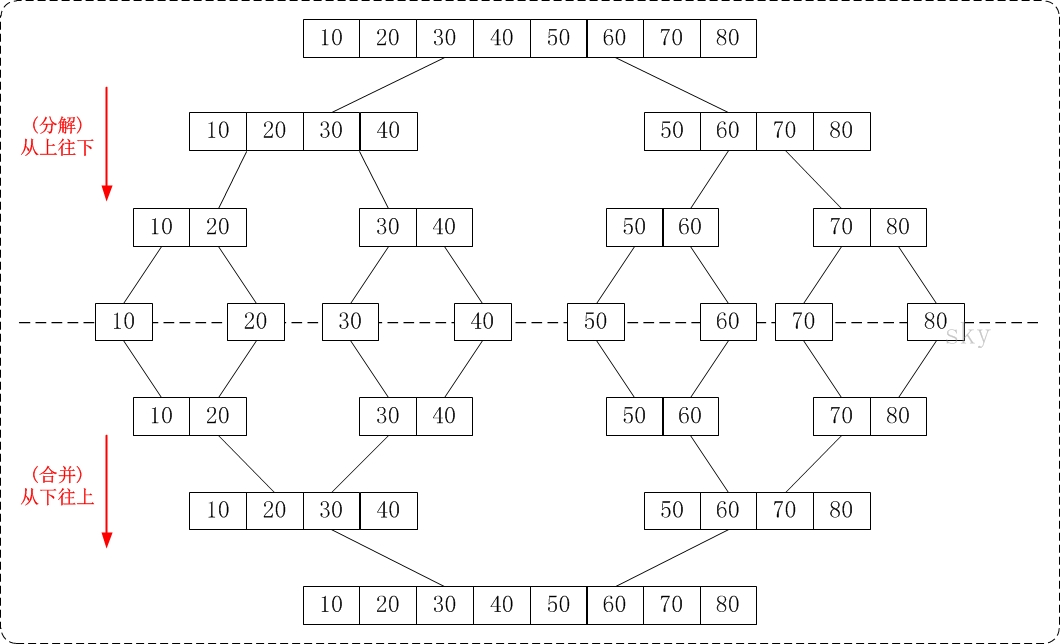
java代码：

    /**
     * 归并排序：不是原地排序，时间复杂度O(n*longN)，稳定排序
     *
     * @param arr
     * @return
     */
    public static int[] guibing(int[] arr) {
        if (arr.length == 1) {
            return arr;
        }
        int mod = arr.length / 2;
        int[] a = new int[mod];
        int[] b = new int[arr.length - mod];
        System.arraycopy(arr, 0, a, 0, mod);
        System.arraycopy(arr, mod, b, 0, arr.length - mod);
        return hebing(guibing(a), guibing(b));
    }

  /**
     * 两个有序数组合并
     *
     * @param a
     * @param b
     * @return
     */
    public static int[] hebing(int[] a, int[] b) {
        int[] result = new int[a.length + b.length];
        int index_a = 0, index_b = 0;
        for (int i = 0; i < result.length; i++) {
            if (index_a >= a.length) {
                result[i] = b[index_b++];
                continue;
            }
            if (index_b >= b.length) {
                result[i] = a[index_a++];
                continue;
            }
            if (a[index_a] <= b[index_b]) {
                result[i] = a[index_a++];
            } else {
                result[i] = b[index_b++];
            }
        }
        return result;
    }