CF1096F Inversion Expectation

https://codeforces.com/problemset/problem/1096/F

题意：

给你一个长为 n 的排列，若某一位为 −1 则这一位是不确定的。每种可能的排列出现的概率相等。求期望逆序对数对 998244353 取模的结果。

---

 

让我们把问题拆成四个小问题

问题 1. 两个都是不确定的位置组成的逆元。每对位置要么构成逆元，要么不构成逆元。而且这两种方案数是相等的（只要把两个数字交换一下就能构造出了）因此每对这样的位置都能贡献二分之一个逆序对，所以这部分的答案就是

 

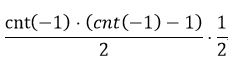
问题 2 和 3.由一个未知数和一个已知数组成的逆序对。让我们先看左边未知、右边已知的这种分类，对应的另一种的处理方法是类似的。对于每一个已知的数字，计算它左侧的所有未知位置数为lftx，以及未确定数中大于这个数的总数gtx。只有当这些数字出现在前面才能贡献价值，每个位置上平均出现gtx/cnt(-1)个，而前面一共有lftx个位置，因此总贡献就是lftx*gtx/cnt(-1)，把他们都加到ans中去

问题 4.由两个已知数组成的逆序对。这个问题十分经典，在这里就不多叙述了。统计出答案累加即可

总复杂度：

O(nlogn)

其中除了最后一种问题，其他问题都可以用O(n)的复杂度解决。

我认为问题的拆分和转化是很重要的，如果找错了切入点或者没有恰当的分类，都很难流畅的解决问题

转载于:https://www.cnblogs.com/2017SSY/p/10209998.html