神经网络优化（二） - 正则化

在机器学习中，有时候我们基于一个数据集训练的模型对该模型的正确率非常高，而该模型对没有见过的数据集很难做出正确的响应；那么这个模型就存在过拟合现象。

为了缓解或避免过拟合现象，我们通常用的方法是采用正则化方法（Regularization）。

1 正则化基本理解

 正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据的噪声（注：一般不正则化 b，仅正则化 w ）

 

2 loss(w)函数的两种表述方式

# 表达方式1
loss(w) = tf.contrib.l1_regularizer(regularizer)(w)
# 表达方式2
loss(w) = tf.contrib.l2_regularizer(regularizer)(w)

其对应的数学表达式为

 将正则化计算好的 w 添加到 losses 中，

tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w)

再将 losses 中的所有值相加，并将其与交叉熵 cem 相加形成最终的 loss 值

loss = cem + tf.add_n(tf.get_collection('losses'))

 3 示例

已经有如下神经网络结构

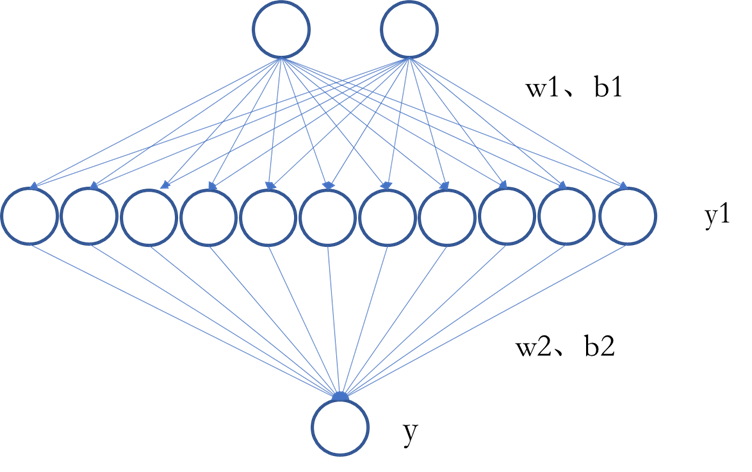
由神经网络结构可知，

w1 - 2行11列矩阵

b1 - 11行1列矩阵

w2  - 11行1列

b2 - 1行1列

# 0导入模块 ，生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
BATCH_SIZE = 30
seed = 2

# 基于seed产生随机数
rdm = np.random.mtrand.RandomState(seed)
# 随机数返回300行2列的矩阵，表示300组坐标点（x0,x1）作为输入数据集
X = rdm.randn(300, 2)
# 制作标签，
# 从X中任选一行，若坐标点平方和<2,则Y_=1,否则Y_=0
Y_ = [int(x0*x0 + x1*x1 < 2) for (x0, x1) in X]
# 为便于可视化区分，将Y_中1赋值‘red’，0赋值‘blue’
Y_c = [['red' if y else 'blue'] for y in Y_]
# 对数据集X和标签Y进行shape整理，
# 第一个元素为-1表示，该参数不决定reshape形状，由第二、三……参数决定
# 第二个元素表示多少列，把X整理为n行2列，把Y整理为n行1列
X = np.vstack(X).reshape(-1, 2)
Y_ = np.vstack(Y_).reshape(-1, 1)
# print(X)
# print(Y_)
# print(Y_c)


# 用plt.scatter画出数据集X各行中第0列元素和第1列元素的点即各行的（x0，x1），
# 用各行Y_c对应的值表示颜色（c是color的缩写）
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
# plt.show()

# 定义前向传播过程
# 定义神经网络的待优化参数w、正则L2优化w值
def get_weight(shape, regularizer):
    w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
    return w
# 定义神经网络的参数b
def get_bias(shape):
    b = tf.Variable(tf.constant(0.01, shape=shape))
    return b
# 定义前向传播数据集及标签 placeholder占位
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

# 两层网络，第一层网络W值，[2,11]两个特征值
w1 = get_weight([2, 11], 0.01)
b1 = get_bias([11])
print(tf.matmul(x, w1) + b1)
# tf.nn.relu()返回与参数same type的张量Tensor
# 该处想不通，tf.matmul(x,w1).shape为(?,11)
# 而b1.shape为(11,)，为什么能加？因为广播的原因？
# 知道原因的给俺留个言，谢谢
y1 = tf.nn.relu(tf.matmul(x, w1)+b1)
# 两层网络，第二层w值
w2 = get_weight([11, 1], 0.01)
b2 = get_bias([1])
y = tf.matmul(y1, w2)+b2


# 定义损失函数（此处用均方误差）
loss_mse = tf.reduce_mean(tf.square(y-y_))
# 正则化处理
loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))

为什么tf.matmul(x,w1).shape （？，11）与 b1.shape（11，） 的值不一样还能加和

一直没有想通。谁知道，烦请留言说一下，谢谢

3.1 不含正则化

# 定义反向传播方法：不含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_mse)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 300
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})
        if i % 2000 == 0:
            loss_mse_v = sess.run(loss_mse, feed_dict={x:X, y_:Y_})
            print("After %d steps, loss is: %f" %(i, loss_mse_v))
    # xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成二维网格坐标点
    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    # 将xx , yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
    grid = np.c_[xx.ravel(), yy.ravel()]
    # 将网格坐标点喂入神经网络 ，probs为输出
    probs = sess.run(y, feed_dict={x: grid})
    # probs的shape调整成xx的样子
    probs = probs.reshape(xx.shape)
    print("w1:\n", sess.run(w1))
    print("b1:\n", sess.run(b1))
    print("w2:\n", sess.run(w2))
    print("b2:\n", sess.run(b2))

plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

运行

全部结果

After 0 steps, loss is: 17.276403
After 2000 steps, loss is: 6.742686
After 4000 steps, loss is: 2.918497
After 6000 steps, loss is: 1.357461
After 8000 steps, loss is: 0.704671
After 10000 steps, loss is: 0.347484
After 12000 steps, loss is: 0.158813
After 14000 steps, loss is: 0.087291
After 16000 steps, loss is: 0.075287
After 18000 steps, loss is: 0.073110
After 20000 steps, loss is: 0.071862
After 22000 steps, loss is: 0.070709
After 24000 steps, loss is: 0.069558
After 26000 steps, loss is: 0.068642
After 28000 steps, loss is: 0.067907
After 30000 steps, loss is: 0.067117
After 32000 steps, loss is: 0.066362
After 34000 steps, loss is: 0.065661
After 36000 steps, loss is: 0.064930
After 38000 steps, loss is: 0.064223
w1:
 [[-0.9773499   0.22049664 -0.65066797 -1.1784189   0.3604557  -0.4094967
  -0.7772123  -0.19874994 -0.16293146  0.6851439   0.07392277]
 [ 0.703745    1.4519942   1.1566342  -0.23761342  0.00913512  1.2041332
  -1.1184367  -0.6418423  -0.06947413 -0.7816815   0.09283698]]
b1:
 [-0.59472626 -0.6971679  -0.2131384   0.06717522 -0.68735933 -0.19442134
 -0.52873707  1.0804558   0.7781985  -0.47215533 -0.38051093]
w2:
 [[-0.12292398]
 [-0.3172334 ]
 [-0.6289589 ]
 [-0.25597483]
 [ 1.6608844 ]
 [ 0.70720905]
 [-0.504943  ]
 [ 0.32134637]
 [ 0.9881266 ]
 [-0.6332165 ]
 [ 0.43281034]]
b2:
 [0.05319614]

不含正则化的运行结果

 

 

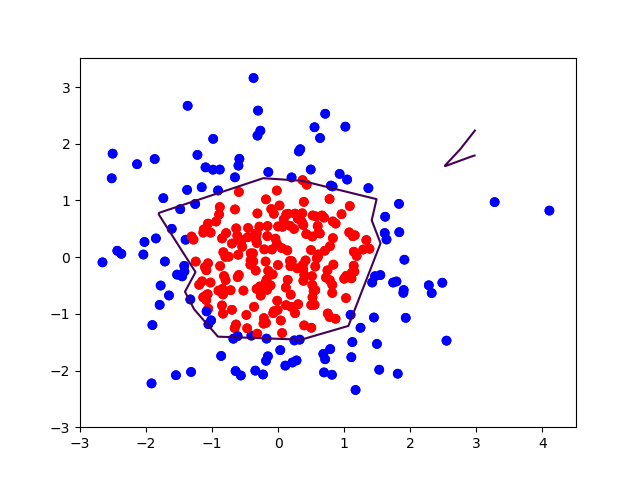
 3.2 含正则化

# 定义反向传播方法：包含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 300
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 2000 == 0:
            loss_v = sess.run(loss_total, feed_dict={x: X, y_: Y_})
            print("After %d steps, loss is: %f" % (i, loss_v))

    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)
    print("w1:\n", sess.run(w1))
    print("b1:\n", sess.run(b1))
    print("w2:\n", sess.run(w2))
    print("b2:\n", sess.run(b2))

plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

运行

结果的全部代码

After 0 steps, loss is: 4.159994
After 2000 steps, loss is: 0.608495
After 4000 steps, loss is: 0.265381
After 6000 steps, loss is: 0.192880
After 8000 steps, loss is: 0.177134
After 10000 steps, loss is: 0.166259
After 12000 steps, loss is: 0.156994
After 14000 steps, loss is: 0.149236
After 16000 steps, loss is: 0.142333
After 18000 steps, loss is: 0.135975
After 20000 steps, loss is: 0.129736
After 22000 steps, loss is: 0.123473
After 24000 steps, loss is: 0.117122
After 26000 steps, loss is: 0.113461
After 28000 steps, loss is: 0.110417
After 30000 steps, loss is: 0.107875
After 32000 steps, loss is: 0.105741
After 34000 steps, loss is: 0.103761
After 36000 steps, loss is: 0.101936
After 38000 steps, loss is: 0.100259
w1:
 [[ 0.46141306 -0.47860026 -0.04003494 -0.2274962   0.16311681  0.14396985
   0.28831962 -0.20041619  0.17948255  0.6495893   0.2442107 ]
 [ 0.13395171 -0.4907351  -0.23803091  0.01938409 -0.30272898 -0.32200766
  -0.07292039  0.72900414 -0.26523823 -0.775128    0.23733395]]
b1:
 [-0.21913818 -0.297991   -0.0171856   0.40895092 -0.26794708  0.23960082
 -0.00739933 -0.38744184  0.5618932  -0.17630258  0.27928215]
w2:
 [[-0.4492314 ]
 [-1.0002819 ]
 [ 0.13530669]
 [ 0.4237453 ]
 [-0.39334002]
 [ 0.34084177]
 [-0.24576233]
 [-0.6192874 ]
 [ 0.7040131 ]
 [-0.58746487]
 [ 0.22011437]]
b2:
 [0.40935752]

含正则化的结果代码

 

其实这章节没有完全明白，尚留下一些疑问。