Timus 1114. Boxes

最新推荐文章于 2025-09-08 16:47:15 发布

转载最新推荐文章于 2025-09-08 16:47:15 发布 · 137 阅读

文章标签：

#c# #c/c++

解决Timus1114.Boxes问题，计算不同颜色球放入盒子的所有可能组合数。使用组合数学方法，给出C#及C++实现方案。

Timus 1114. Boxes 要求计算出将两种颜色的球放到盒子中的各种组合的数目。

1114. Boxes

Time Limit: 0.6 second
Memory Limit: 16 MB

N boxes are lined up in a sequence (1 ≤ N ≤ 20). You have A red balls and B blue balls (0 ≤ A ≤ 15, 0 ≤ B ≤ 15). The red balls (and the blue ones) are exactly the same. You can place the balls in the boxes. It is allowed to put in a box, balls of the two kinds, or only from one kind. You can also leave some of the boxes empty. It's not necessary to place all the balls in the boxes. Write a program, which finds the number of different ways to place the balls in the boxes in the described way.

Input

Input contains one line with three integeres N, A and B separated by space.

Output

The result of your program must be an integer writen on the only line of output.

Sample

input	output
2 1 1	9

Problem Source: First competition for selecting the bulgarian IOI team.

解答如下(C＃语言)：

1 using System;
2
3 namespace Skyiv.Ben.Timus
4 {
5    // http://acm.timus.ru/problem.aspx?space=1 &num=1114
6    sealed class T1114
7   {
8      static void Main()
9     {
10        string [] ss = Console.ReadLine().Split();
11        ulong n = ushort .Parse(ss[ 0 ]);
12        ulong a = ushort .Parse(ss[ 1 ]);
13        ulong b = ushort .Parse(ss[ 2 ]);
14       Console.WriteLine(F(n, a) * F(n, b));
15     }
16
17      static ulong F( ulong n, ulong m)
18     {
19        ulong v = 1 ;
20        for ( ulong i = 1 ; i <= n; i ++ ) v = v * (m + i) / i;
21        return v;
22     }
23   }
24 }

这道题就是一个组合数学问题。题目说，你有 N (1 ≤ N ≤ 20) 个盒子，A (0 ≤ A ≤ 15) 个红色的球和 B (0 ≤ B ≤ 15) 个蓝色的球。这些球可以放到盒子里面，也可以不放到盒子里面，一个盒子可以放任意多个球。问总共有多少种不同情形。

由于球可以放到盒子里面，也可以不放到盒子里面，所以红球和盒子总共有 C( N + A, A ) 种不同的情形。同样，蓝球和盒子总共有 C( N + B, B ) 种不同的情形。所以，最终的答案就是 C( N + A, A) * C( N + B, B ) 。这里，C( n, m ) 表示从 n 个不同的物品中任意取出 m 个的组合数，公式是 C( n, m ) = n! / (n - m)! / m!。以上程序中的 F( n, m ) = C( n + m, m)。

要注意的是，当输入为 N = 20，A = 15，B = 15 时，输出是 10549134770590785600，这个数已经大于 2⁶³ - 1，所以要使用 ulong 数据类型。如果使用 C/C++ 语言，因为 Timus Online Judge 使用的是 Visual C++ 编译器，所以要使用 unsigned __int64 数据类型。如果在 Sphere Online Judge 答题的话，因为其编译器是 gcc，所以要使用 unsigned long long 数据类型。C++ 语言的程序如下所示(如果是 gcc 编译器则去掉第 2 行开头的“//”)：

1 #include < iostream >
2 // #define __int64 long long
3
4 unsigned __int64 f(unsigned __int64 n, unsigned __int64 m)
5 {
6   unsigned __int64 v = 1 ;
7    for (unsigned __int64 i = 1 ; i <= n; i ++ ) v = v * (m + i) / i;
8    return v;
9 }
10
11 int main()
12 {
13   unsigned __int64 n, a, b;
14   std::cin >> n >> a >> b;
15   std::cout << f(n, a) * f(n, b) << std::endl;
16 }

本程序的运行时间如下：

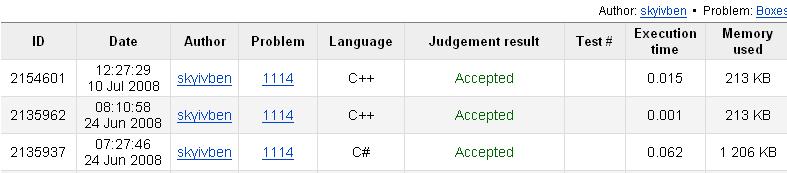
有点奇怪的是，Visual C++ 编译器也可以使用 unsigned long long，但是速度却比使用 unsinged __int64 慢了 15 倍。如上图所示，ID = 2154601 的记录就是使用 unsinged long long，运行时间为 0.015 秒。而 ID = 2135962 的记录使用 unsinged __int64，运行时间为 0.001 秒。不知是什么原因。照理说，__int64 应该和 long long 是一样的。