一、折半查找

1、条件：待查表为有序表。

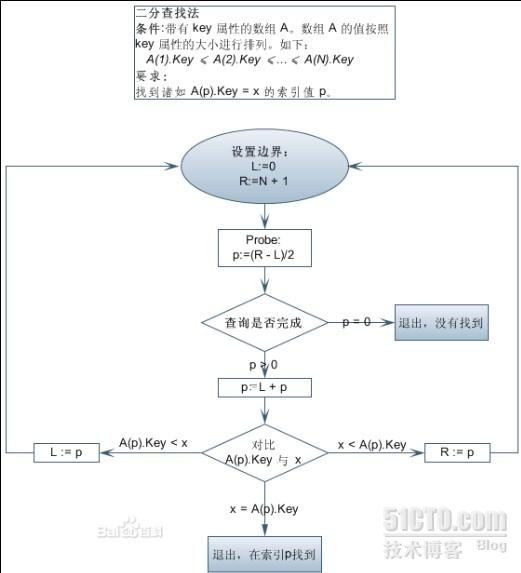
2、原理：首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

110147323.jpg

3、code

int Binary_Search(int *a,int n,int key)
{
    int low,high,mid;
    low=1;    /*定义最低下标为记录首位*/
    high=n;
    while(low<=hight)
    {
        mid=(low+high)/2;    /*折半*/
        if (key<a[mid])        /*若查找值必中值小*/
            high=mid-1;        /*最高下标调整到比中位小一的下标*/
        else if (key>a[mid])    /*若查找值必中值大*/
            low=mid+1;           /*最低下标调整大必中位大一的下标*/
        else 
            return mid;     /*找到值相等的，返回该下标*/
    }
    return 0;    /*若a中没有key则返回0*/
}

二、差值查找

1、条件：待查表为有序表。

2、原理：原理同折半查找，只是将折半的算法mid=(low+high)/2（也就是mid=low+(1/2)*(high-low)）改为mid=low+[(key-a[low])/(a[hight]-a[low])]*(high-low)。

3、code

将折半查找的第8行代码改为 mid=low+[(key-a[low])/(a[hight]-a[low])]*(high-low)。

三、斐波那契查找

1、条件：待查表为有序表。

2、原理：利用斐波那契数列的数组进行分割待查的有序表。斐波那契数组F[0]=1，F[1]=1，F[n]=F[n-2]+F[n-1]。

3、code

int Fibonacci_Search(int *a,int n,int key)
{
    int low,high,mid,i,k;
    low=1;    /*定义最低下标为记录的首位置*/
    high=n;    /*定义最高下标为记录末位置*/
    k=0;
    while(n>F[k]-1)    /*计算n位于斐波那契数列的位置*/
        k++;
    for(i=n;i<F[k]-1;i++)    /*将不满的数值补全*/
        a[i]=a[n];
    while(low<=high)
    {
        mid=low+F[k-1]-1;    /*计算当前分隔的下标，数组a共F[k]个元素，现在分为F[k-1]个和F[k-2]个元素*/
        if(key<a[mid])    /*若查找记录小于当前分隔记录*/
        {
            high=mid-1;    /*最高下标调整到分隔下标mid-1处*/
            k=k-1;    /*斐波那契数列的下标减一，此时数组a可以缩短为从low到以后的F[k]个了*/
        }
        else if(key>a[mid])
        {
            low=mid+1;    /*最低下标调整到分隔下标mid+1处*/
            k=k-2;         /*斐波那契数列的下标减二，此时数组a可以缩短为从mid+1到以后的F[k]个了*/
        }
        else
        {
            if(mid<=n)
                return mid;    /*若相等则说明mid即为查找到的位置*/
            else
                return n;    /*若mid>n说明是补全数值，返回n*/
        }
    }
    return 0;
}