补一下dp的思路: dp[i][j]表示第 i 分钟转 j 次所得到的最大值。很容易得到这个dp的推导式。
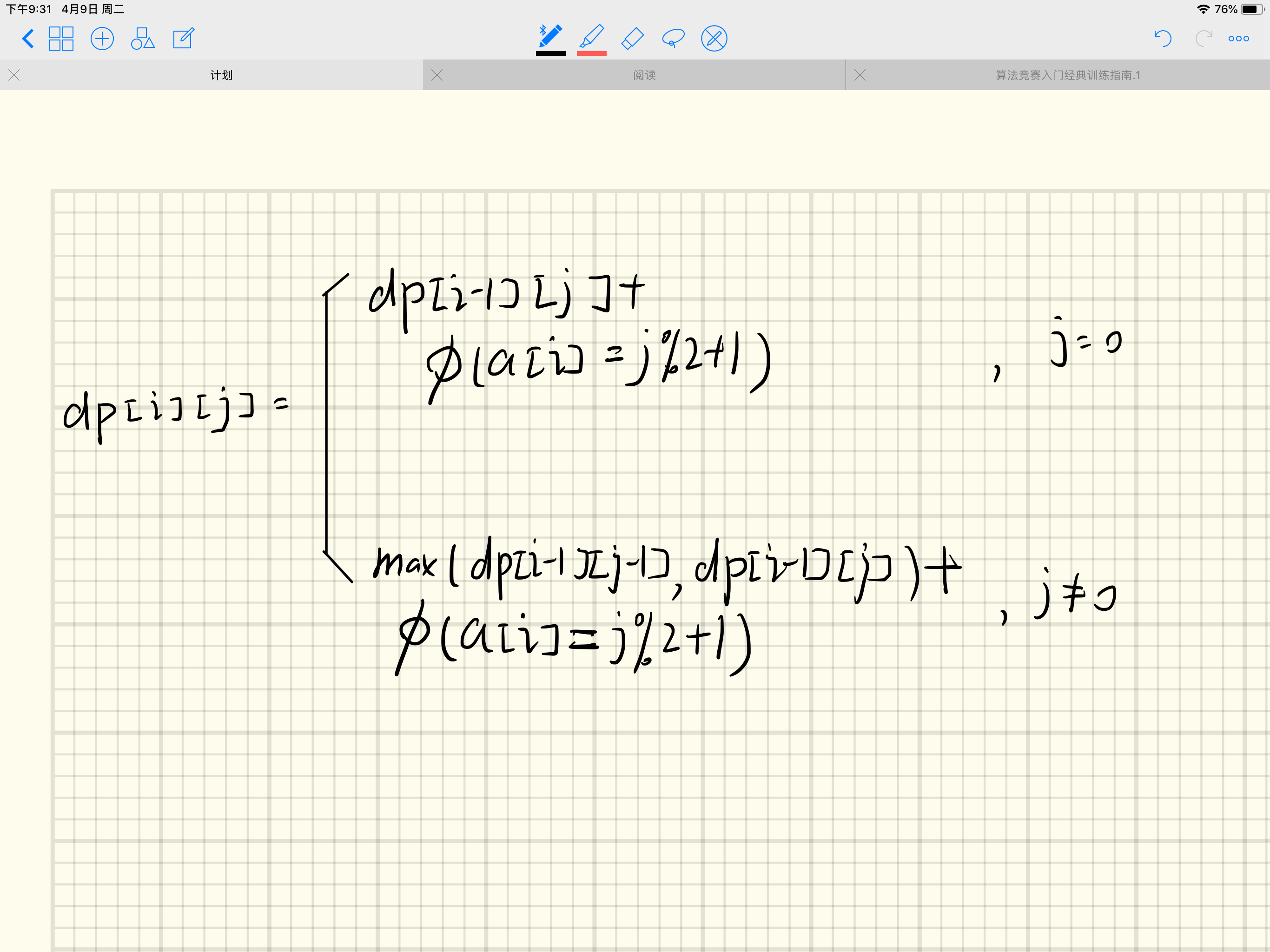
图中¢()函数表示成立为1, 不成立为0的函数。
#include<cmath>
#include<iostream>
using namespace std;
int dp[1010][40], t, w;
int a[1010];
int ans;
int main(){
cin>>t>>w;
for(int i=1;i<=t;++i){
cin>>a[i];
for(int j=0;j<=w;++j)
{
if(j==0)dp[i][j]=dp[i-1][j];
else dp[i][j]=max(dp[i-1][j], dp[i-1][j-1]);
if(a[i]==j%2+1)dp[i][j]++;
}
}
for(int i=0;i<=w;++i)
ans=max(ans, dp[t][i]);
cout<<ans<<endl;
}




 本文深入解析了动态规划(DP)算法的实现思路,通过具体案例展示了如何利用DP算法求解最大值问题。文章提供了完整的代码示例,详细解释了状态转移方程的推导过程。
本文深入解析了动态规划(DP)算法的实现思路,通过具体案例展示了如何利用DP算法求解最大值问题。文章提供了完整的代码示例,详细解释了状态转移方程的推导过程。
















 507
507

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








